线性表

线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储

顺序表

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删查改

（顺序表就是数组，但是是在数组的基础上，另外还要求数据是从头开始存储 ，并且数据是连续存储的，不能跳跃间隔）

顺序表一般可以分为：

• 静态顺序表：使用定长数组存储元素
• 动态顺序表：使用动态开辟的数组存储

接口实现

尾插

 typedef struct SeqList
{
	SLDaTaType * a;
	int size; // 数组中存了多少个数
	int capacity; //数组实际容量个数
}SL;

void SeqListPushBack(SL* ps, SLDaTaType x)   //尾插
{
	assert(ps);

	 //空间不足则扩容 
	if (ps->capacity == ps->size)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;   // 若空间为0  就放4个字节  ， 否则capacity *2  
		SLDaTaType * tmp  = ( SLDaTaType* )realloc(ps->a, newcapacity * sizeof(SLDaTaType));
		if (tmp == NULL) //开辟失败
		{
			printf("realloc fail \n");
			exit(-1);  
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
	ps->a[ps->size] = x;  // 空间足够 
	ps->size++;
} 

---

void SeqListDestory(SL* ps) //销毁 ，防止内存泄露
{
	assert(ps);

	free(ps->a);
	ps->a = NULL; 
	ps->size = ps->capacity = 0;
}

尾删

void SeqListPopBack(SL* ps)// 尾删
{
	assert(ps);

	// ps->a[ps->size - 1] = 0;
	assert(ps->size > 0);
	ps->size--;  
}

头插

最后一个数向后挪动

void SeqListPushFront(SL* ps, SLDaTaType x) // 头插
{
	assert(ps);

	  // 挪动 
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
}

头删

void SeqListPopFront(SL* ps) // 头删
{
	assert(ps);

	assert(ps->size > 0);
	//挪动数据
	int begin =1 ;
	while (begin<=ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;

	}
	ps->size--;
}

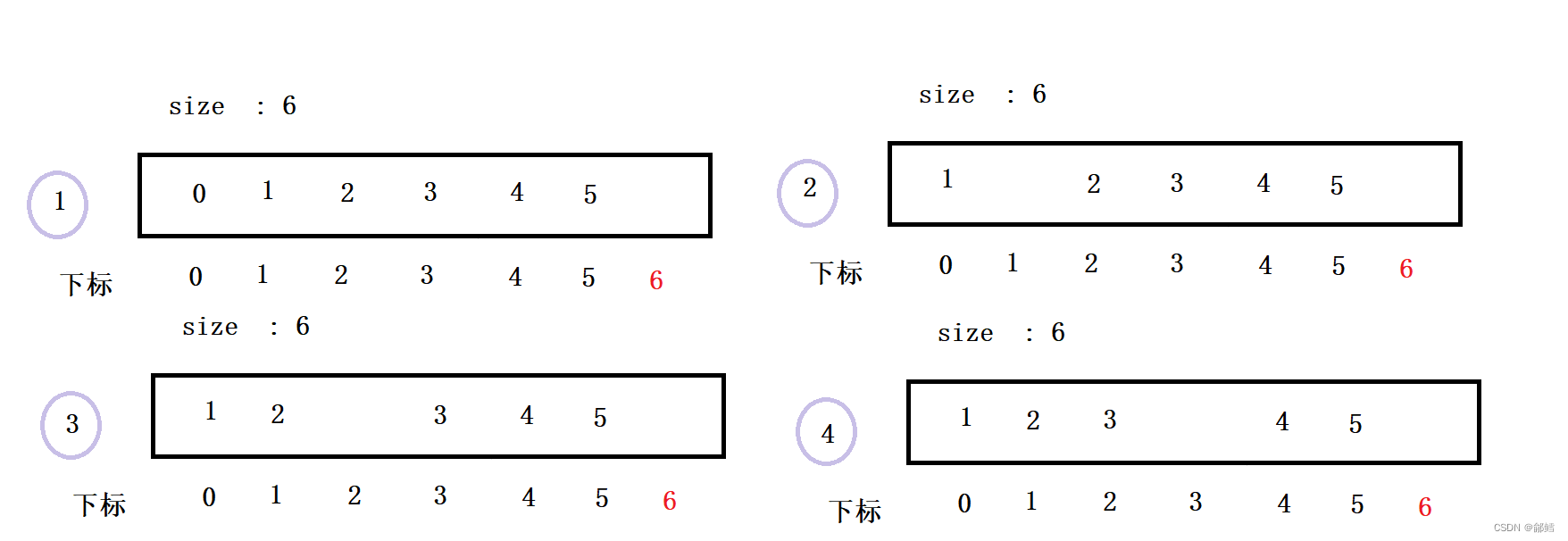
找到了返回x位置下标 若没有找到返回-1

int SeqListFind(SL* ps, SLDaTaType  x)
{
	assert(ps);

	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	
	}
	return -1; 
}

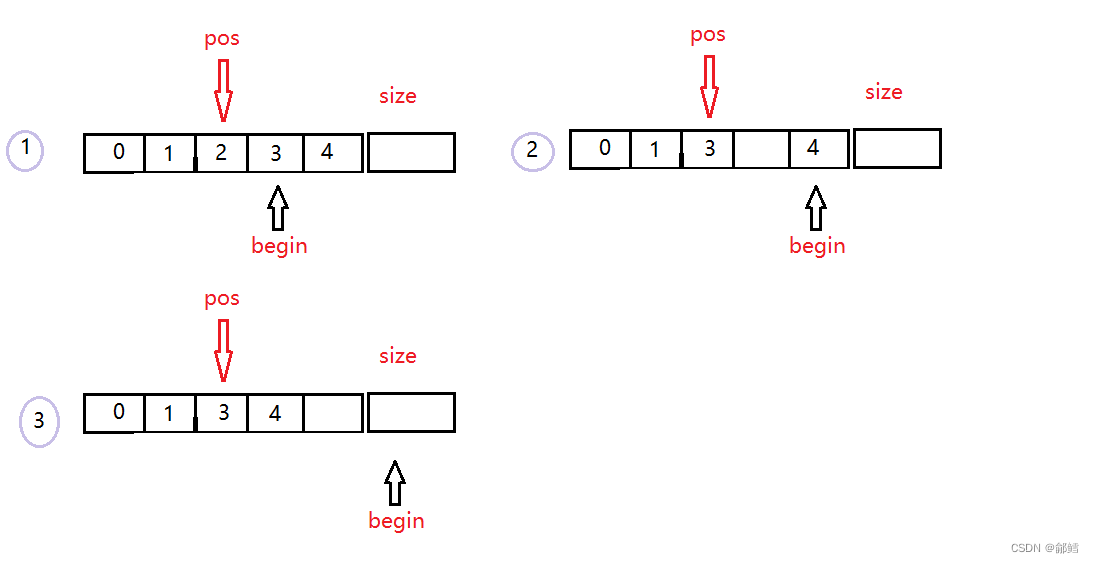
指定位置插入

void SeqListInsert(SL* ps, int pos, SLDaTaType x) // 指定位置插入
{
	assert(ps);

	assert(pos >=0 && pos <= ps->size);
	int end = ps->size -1 ;
	SeqListCheckCapacity(ps); //防止后面空间不足 挪动的时候越界访问
	while (end >= pos)
	{
		//挪动 
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	//插入数据
	ps->a[pos] = x;
	ps->size++;
}

指定位置删除

void SeqListErase(SL* ps, int pos) // 指定位置删除
{
	assert(ps);

	assert(pos >= 0 && pos < ps->size);
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		begin++;
	}
	ps->size--;
}

练习

https://leetcode.cn/problems/remove-element/

思路一 ： 找到所有的val ，一次挪动数据覆盖删除
时间复杂度最坏的情况是数组中绝大部分值是val甚至全部是val

假设数组中有N个数据 第一个数据是val ，这时候需要挪动N-1 个元素 ，
第二个数据是val ，得挪动N-2个元素
依次类推 第n个数据是val ，得挪动N-n
不难发现是一个等差数列 ，时间复杂度为O（N^2)

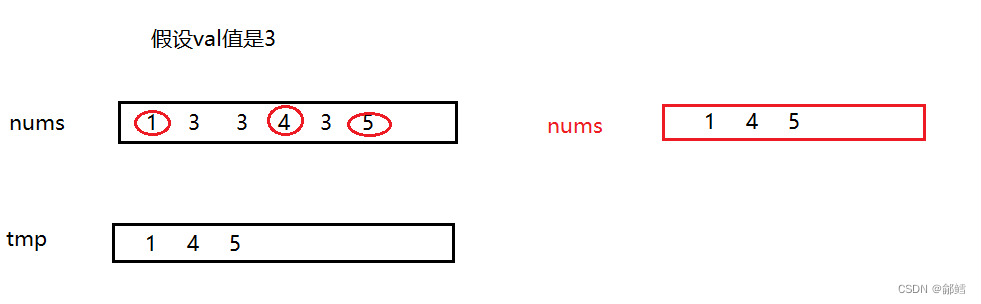
思路二：

依次遍历整个数组 ，把不是val 得值放到tmp 数组中 ，再把tmp数组得值拷贝到nums数组中 ，这样我们将时间复杂度优化到 O（N） ，但是空间复杂度 为O(N)

思路三 src去找nums 数组中不是val 的值 ， 放到dst 指向的位置中 ，再++src ++dst
这样时间复杂度是O（N） ，空间复杂度是O（1）

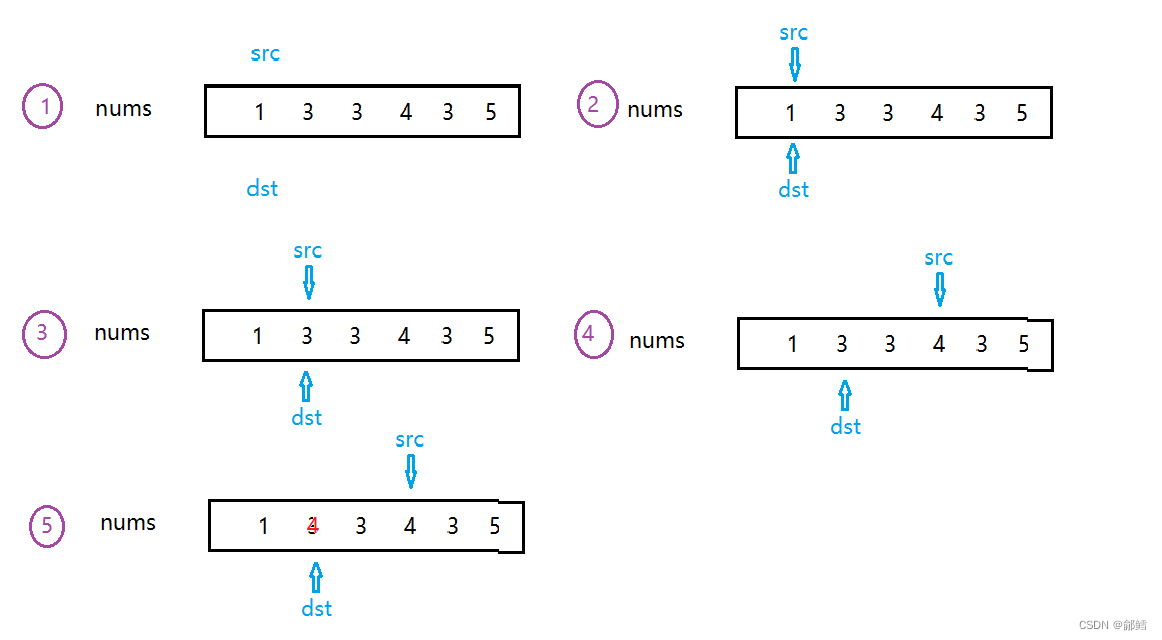
int removeElement(int* nums, int numsSize, int val)
{
 int src = 0;
 int dst =0 ;
 while (src < numsSize )
 {
     if( nums[src]!=val )
   {
        nums[dst] = nums[src];
     src++ ;
     dst ++ ;    
   }
   else 
   {
       src++;
   }
 }
 return dst;
}

https://leetcode.cn/problems/remove-duplicates-from-sorted-array/

---

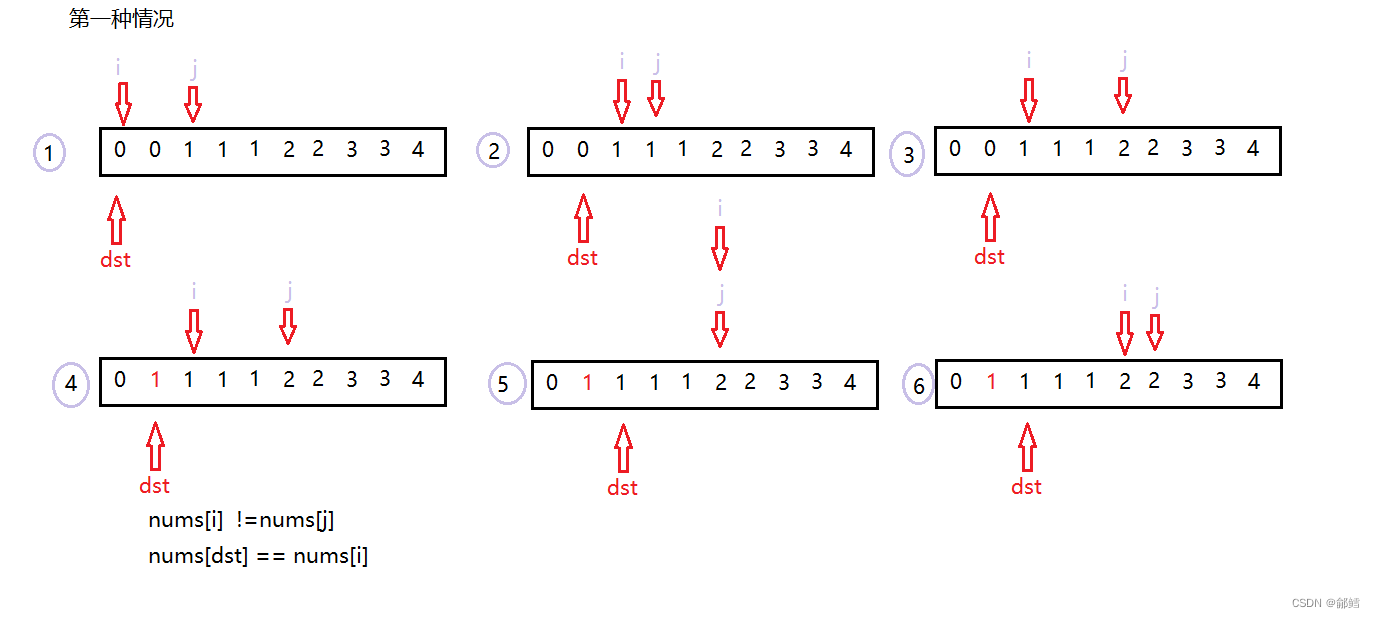
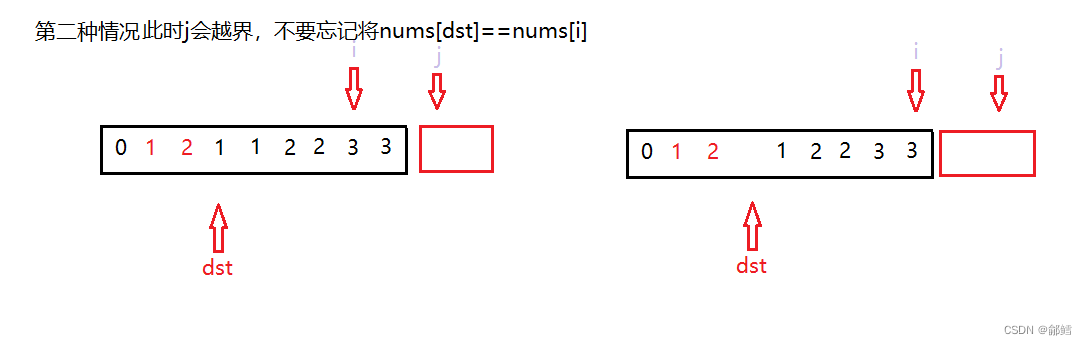
int removeDuplicates(int* nums, int numsSize)
{
    if (numsSize==0  )
    {
        return 0 ;
    }
    int j =1;
    int i = 0;
    int dst = 0 ;
     // j 没有越界 
     while( j<numsSize)
     {
          // 判断 i和j是否相等 不相等就继续往下找
          if(nums[i] ==nums[j])
          {
              j++ ;
          }
          else   // 不相等就把 nums[dst]=nums[i]
          {
           nums[dst]=nums[i];
           i=j;
           dst++;
           j++;
          }
     }
     //j越界
     nums[dst]=nums[i];
     ++dst;
     return dst ; // 返回dst的下标
}

如果你觉得这篇文章对你有帮助，不妨动动手指给点赞收藏加转发，给鄃鳕一个大大的关注
你们的每一次支持都将转化为我前进的动力！！！