💃🏼 本人简介：男
👶🏼 年龄：18
🤞 作者：那就叫我亮亮叭
📕 专栏：蓝桥杯试题

1. 题目描述

从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

• 输入格式
  输入一个整数 n。

• 输出格式

  • 每行输出一种方案。
  • 同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。
  • 对于没有选任何数的方案，输出空行。
  • 本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

• 数据范围
  1≤n≤15

• 输入样例：

3

• 输出样例：

3
2
2 3
1
1 3
1 2
1 2 3

2. 思路解释

2.1 时间复杂度

本题需要转化一下思路，根据样例，我们所要输出的内容为所有数据选与不选排列组合的全部方案。所以，每个数据都有选与不选的两种选择，一共1~n有n个数据，所以总共2ⁿ个方案，每次输出长度最长为n，再加上剪枝，则本题的时间复杂度应该不会超过n*2ⁿ。

2.2 递归

递归精髓——从1~n依次遍历考虑选或不选

类似图下这样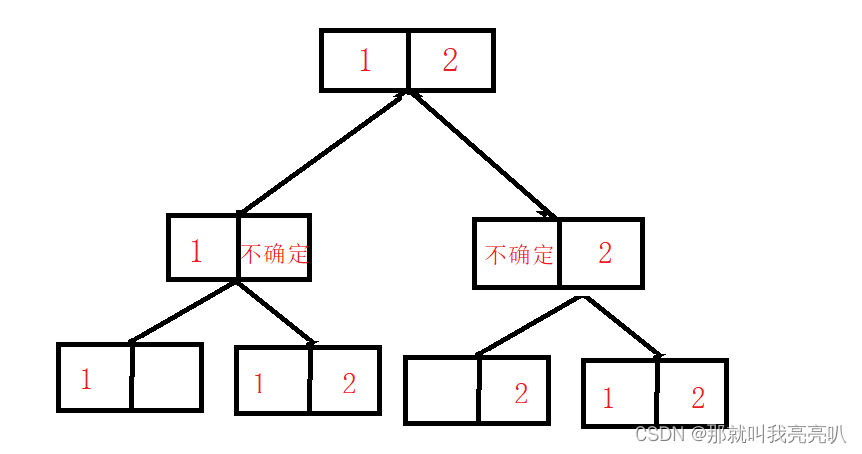
大佬的这张图的思路清晰了！！

3. 代码展示

#include<iostream>
#include<stdio.h>
using namespace std;
const int N = 20;
int n, a[N];
bool vis[N];    //记录i是否被选过

void dfs(int x){
    if(x > n){  //如果超出n的值，则停止搜索，打印前面标记过的数
        for(int i = 1; i <= n; i++){
            if(vis[i]){ 
                cout << i <<" ";
            }
        }   cout << endl;
        return ;
    }   
    
    else{
        vis[x] = true;  //选择这个数字
        dfs(x + 1); //遍历他的下一位
        vis[x] = false;  //不选这个数字
        dfs(x + 1);
    }
}

int main(){
    cin >> n;    
    dfs(1);
    return 0;
}

更多解题思路详见这篇大佬的文章👉AcWing 92. 递归实现指数型枚举详解

最后，感谢大家支持u （^ _ ^）

如果感觉这篇文章对你有帮助的话，不妨三连支持下，十分感谢(✪ω✪)。

printf("点个赞吧*^*");

cout << "收藏一下叭o_o";

System.out.println("评论一下吧^_^");

print("关注一下叭0-0")