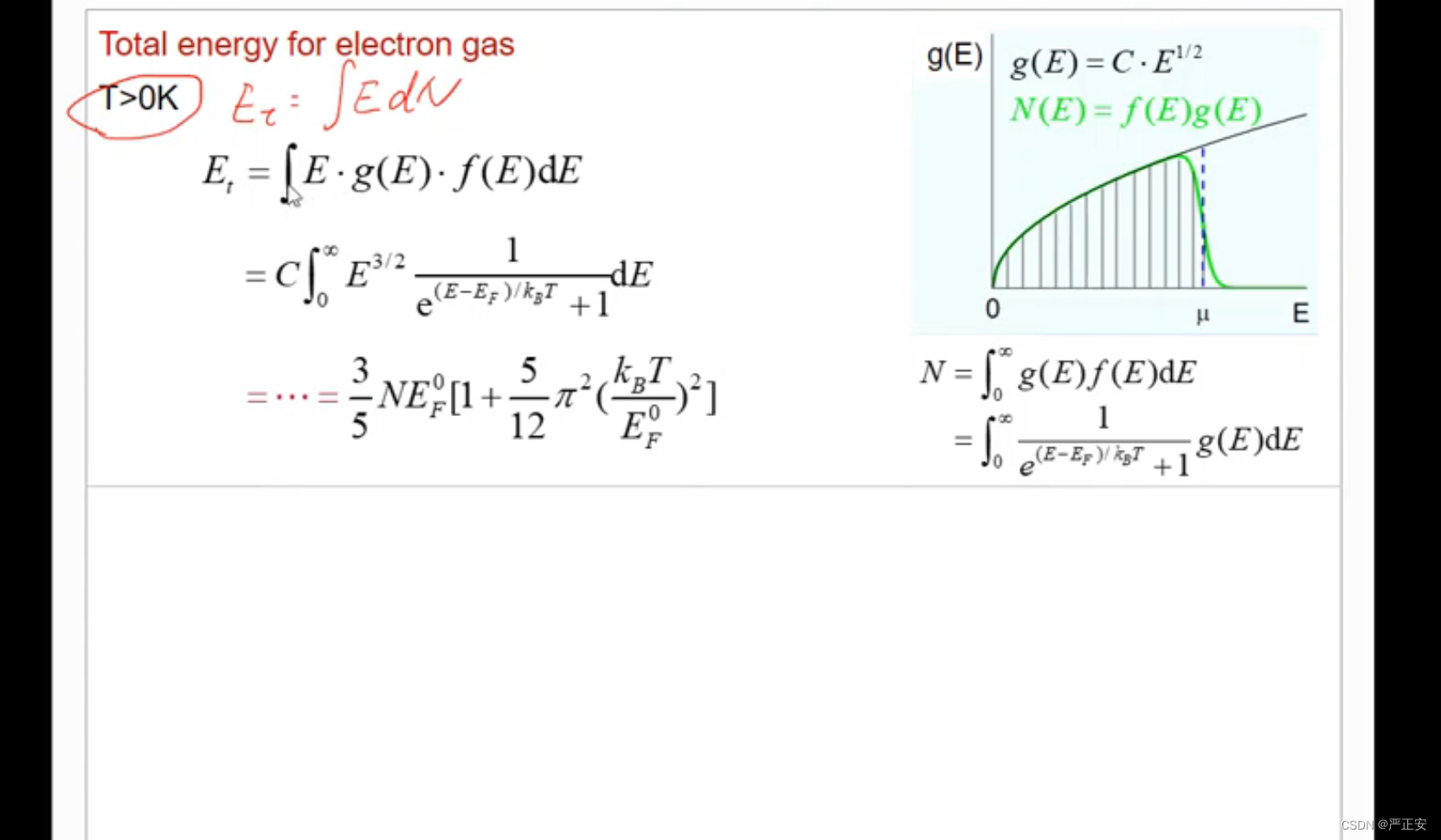
一、负反馈放大电路的方块图表示法

任何负反馈放大电路都可以用图6.3.1所示的方块图来表示，上面一个方块是负反馈放大电路的基本放大电路，下面一个方块是反馈放大电路的反馈网络。负反馈放大电路的基本放大电路是在断开反馈且考虑了反馈网络的负载效应的情况下所构成的放大电路；反馈网络是指与反馈系数 $\dot{F}$ 有关的所有元器件构成的网络。

图中 ${\dot{X}}_i$ 为输入量，${\dot{X}}_f$ 为反馈量，${\dot{X}}_i^{\prime }$ 为净输入量，${\dot{X}}_o$ 为输出量。图中连线的箭头表示信号的流通方向，说明方块图中的信号是单向流通的，即输入信号 ${\dot{X}}_i$ 仅通过基本放大电路传输到输出，而输出信号 ${\dot{X}}_o$ 仅通过反馈网络传递到输入；换言之，${\dot{X}}_i$ 不通过反馈网络传递到输出，而 ${\dot{X}}_o$ 也不通过基本放大电路传递到输入。输入端的圆圈 $\stackrel{◯}{+}$ 表示信号 ${\dot{X}}_i$ 和 ${\dot{X}}_f$ 在此叠加，“+” 号和 “-” 号表明了 ${\dot{X}}_i$、${\dot{X}}_f$ 和 ${\dot{X}}_i^{\prime }$ 之间的关系为$${\dot{X}}_i^{\prime }={\dot{X}}_i-{\dot{X}}_f(\mathrm{6.3.1})$$在信号的中频段，${\dot{X}}_i^{\prime }$、${\dot{X}}_i$ 和 ${\dot{X}}_f$ 均为实数，所以可写成为$$|{\dot{X}}_i^{\prime }|=|{\dot{X}}_i|-|{\dot{X}}_f|或X_i^{\prime }=X_i-X_f(\mathrm{6.3.2})$$在方块图中定义基本放大电路的放大倍数为$$\dot{A}=\frac{{\dot{X}}_o}{{\dot{X}}_i^{\prime }}(\mathrm{6.3.3})$$反馈系数$$\dot{F}=\frac{{\dot{X}}_f}{{\dot{X}}_o}(\mathrm{6.3.4})$$负反馈放大电路的放大倍数（也称闭环放大倍数）为$${\dot{A}}_f=\frac{{\dot{X}}_o}{{\dot{X}}_i}(\mathrm{6.3.5})$$根据式（6.3.3）、（6.3.4）可得$$\dot{A}\dot{F}=\frac{{\dot{X}}_f}{{\dot{X}}_i^{\prime }}(\mathrm{6.3.6})$$$\dot{A}\dot{F}$ 称为电路的环路放大倍数。

二、四种组态电路的方块图

若将负反馈放大电路的基本放大电路与反馈网络均看成两端口网络，则不同反馈组态表明两个网络的不同连接方式。四种反馈组态电路的方块图如图6.3.2所示。其中图（a）所示为电压串联负反馈电路，图（b）所示为电流串联负反馈电路，图（$c$）所示电压并联负反馈电路，图（d）所示为电流并联负反馈电路。

由于电压负反馈电路中 ${\dot{X}}_o={\dot{U}}_o$，电流负反馈电路中 ${\dot{X}}_o={\dot{I}}_o$；串联负反馈电路中，${\dot{X}}_i={\dot{U}}_i$，${\dot{X}}_i^{\prime }={\dot{U}}_i^{\prime }$，${\dot{X}}_f={\dot{U}}_f$；并联负反馈电路中，${\dot{X}}_i={\dot{I}}_i$，${\dot{X}}_i^{\prime }={\dot{I}}_i^{\prime }$，${\dot{X}}_f={\dot{I}}_f$；因此，不同的反馈组态，$\dot{A}$、$\dot{F}$ 和 ${\dot{A}}_f$ 的物理意义不同，量纲也不同，电路实现的控制关系不同，因而功能也就不同，如下表所示$$四种组态负反馈放大电路的比较$$

上表说明，负反馈放大电路的放大倍数具有广泛的含意，而且环路放大倍数 $\dot{A}\dot{F}$ 在四种组态中均无量纲。

三、负反馈放大电路的一般表达式

根据式（6.3.3）、（6.3.4）、（6.3.5）、（6.3.6），可得$${\dot{A}}_f=\frac{{\dot{X}}_o}{{\dot{X}}_i}=\frac{{\dot{X}}_o}{{\dot{X}}_i^{\prime }+{\dot{X}}_f}=\frac{\dot{A}{\dot{X}}_i^{\prime }}{{\dot{X}}_i^{\prime }+\dot{A}\dot{F}{\dot{X}}_i^{\prime }}$$由此得到 ${\dot{A}}_f$ 的一般表达式为：$${\dot{A}}_f=\frac{\dot{A}}{1+\dot{A}\dot{F}}(\mathrm{6.3.7})$$在中频段，${\dot{A}}_f$、$\dot{A}$ 和 $\dot{F}$ 均为实数，因此式（6.3.7）可写成为$$A_f=\frac{A}{1+AF}(\mathrm{6.3.8})$$当电路引入负反馈时，$AF>0$，表明引入负反馈后电路的放大倍数等于基本放大电路放大倍数的 $(1+AF)$ 分之一，而且 $A$、$F$ 和 $A_f$ 的符号均相同。
倘若在分析中发现 $\dot{A}\dot{F}<0$，即 $1+\dot{A}\dot{F}<1$，即 $|{\dot{A}}_f|$ 大于 $|\dot{A}|$，则说明电路中引入了正反馈；而若 $\dot{A}\dot{F}=-1$，使 $1+\dot{A}\dot{F}=0$，则说明电路在输入量为零时就有输出，称电路产生了自激振荡。
若电路引入深度负反馈，即 $1+AF>>1$，则$$A_f\approx \frac{1}{F}(\mathrm{6.3.9})$$表明放大倍数几乎仅仅决定于反馈网络，而与基本放大电路无关。由于反馈网络常为无源网络，受环境温度的影响较小，因而放大倍数获得很高的稳定性。从深度负反馈的条件可知，反馈网络的参数确定后，基本放大电路的放大能力愈强，即 $A$ 的数值愈大，反馈愈深，$A_f$ 与 $1/F$ 的近似程度愈好。
大多数负反馈放大电路，特别是集成运放组成的负反馈放大电路，一般均满足 $1+AF>>1$ 的条件，因而在近似分析中均可认为 $A_f\approx 1/F$，而不必求出 $A$，当然也就不必定量分析基本放大电路了。
应当指出，通常所说的负反馈放大电路是指中频段的反馈极性；当信号频率进入低频段或高频段时，由于附加相移的产生，负反馈放大电路可能对某一特定频率产生正反馈过程，甚至产生自激振荡。