摘要

剑指 Offer 14- I. 剪绳子

剑指 Offer 14- II. 剪绳子 II

343. 整数拆分

一、动态规划解析

这道题给定一个大于1的正整数n，要求将n 拆分成至少两个正整数的和，并使这些正整数的乘积最大化，返回最大乘积。令x是拆分出的第一个正整数，则剩下的部分是 n−x，n−x可以不继续拆分，或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划求解。

创建数组dp，其中dp[i]表示将正整数i拆分成至少两个正整数的和之后，这些正整数的最大乘积。特别地，0不是正整数，1是最小的正整数，0和1都不能拆分，因此 dp[0]=dp[1]=0。

当 i≥2时，假设对正整数i拆分出的第一个正整数是 j(1≤j<i），则有以下两种方案：

将i拆分成j 和i−j的和，且i−j不再拆分成多个正整数，此时的乘积是j×(i−j)；
将i拆分成j和i−j的和，且i−j继续拆分成多个正整数，此时的乘积是j×dp[i−j]。

因此，当j固定时，有 dp[i]=max⁡(j×(i−j),j×dp[i−j])。由于j的取值范围是1到i−1，需要遍历所有的j得到dp[i]的最大值，因此可以得到状态转移方程如下：dp[i]=max(1≤j<i){max(j×(i−j),j×dp[i−j])}。最终得到dp[n]的值即为将正整数n拆分成至少两个正整数的和之后，这些正整数的最大乘积。

package DP;

/**
 * @Classname JZ14
 * @Description TODO
 * @Date 2023/3/1 21:34
 * @Created by xjl
 */
public class JZ14剪绳子 {

    public int cuttingRope(int n) {
        // 定义dp的数组 dp[0]=dp[1]=0
        int[] dp = new int[n + 1];
        for (int i = 2; i <= n; i++) {
            int curMax = 0;
            for (int j = 1; j < i; j++) {
                curMax = Math.max(curMax, Math.max(j * (i - j), j * dp[i - j]));
            }
            dp[i] = curMax;
        }
        return dp[n];
    }
}

复杂度分析

时间复杂度：O(n^2)，其中n是给定的正整数。对于从2到n的每一个整数都要计算对应的dp 值，计算一个整数对应的 dp值需要O(n)的时间复杂度，因此总时间复杂度是O(n^2)。
空间复杂度：O(n)，其中n是给定的正整数。创建一个数组dp，其长度为 n+1

二、数学方法实现

设将长度为n的绳子切为a段：n=n1+n2+...+na，题等价于求解：max(n1×n2×...×na)，以下公式为“算术几何均值不等式” ，等号当且仅当n1=n2=...=na时成立。

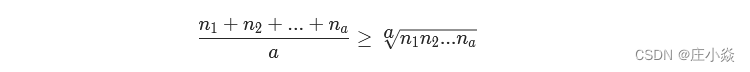
算法流程：

当n≤3时，按照规则应不切分，但由于题目要求必须剪成m>1段，因此必须剪出一段长度为1的绳子，即返回 n−1。
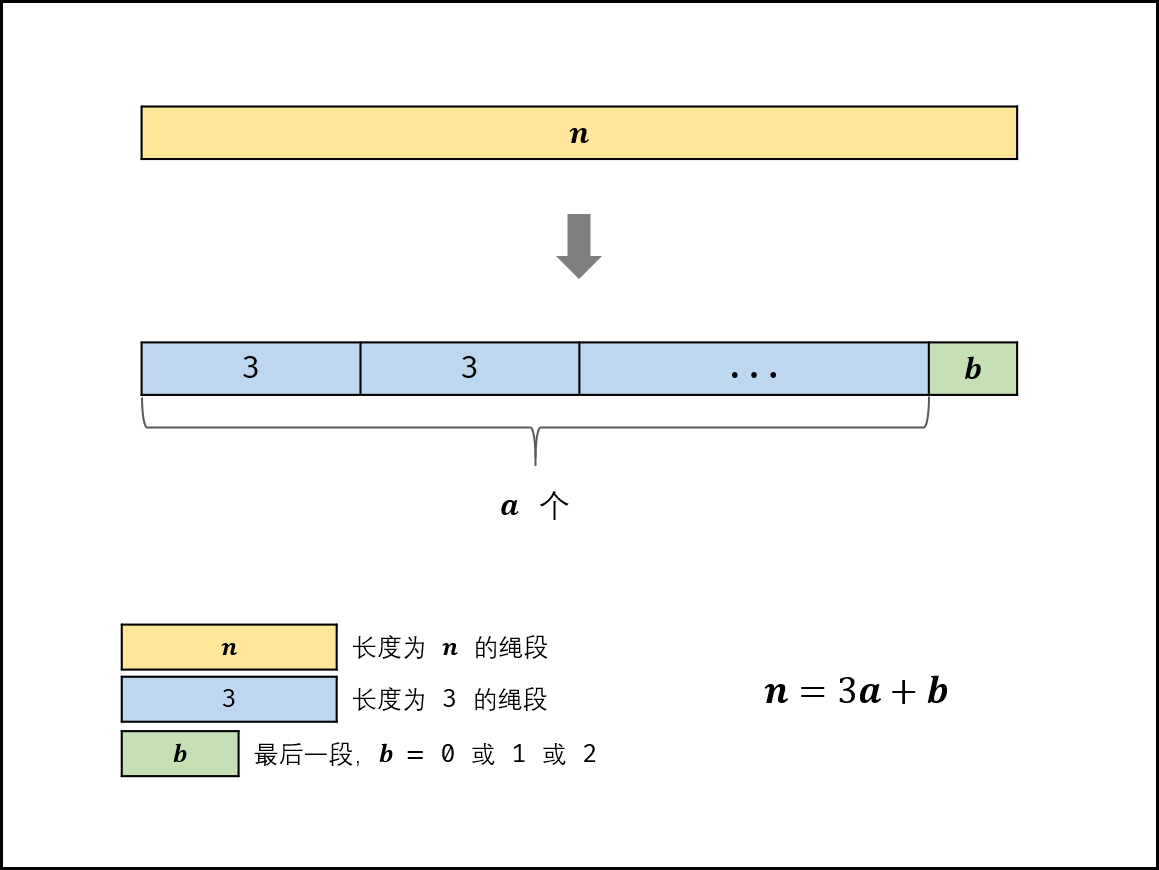
当n>3时，求n除以3的整数部分a和余数部分b （即n=3a+b），并分为以下三种情况：
当 b=0时，直接返回3a；
当 b=1时，要将一个 1+3转换为 2+2，因此返回 3a−1×4；
当 b=2时，返回 3a×2。

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int a = n / 3, b = n % 3;
        if(b == 0) return (int)Math.pow(3, a);
        if(b == 1) return (int)Math.pow(3, a - 1) * 4;
        return (int)Math.pow(3, a) * 2;
    }
}

三、大数越界情况下的求余问题

此题与剪绳子主体等价，唯一不同在于本题目涉及 “大数越界情况下的求余问题” 。

切分规则：

最优：3。把绳子尽可能切为多个长度为3的片段，最后一段绳子长度可能为0,1,2三种情况。
次优：2。若最后一段绳子长度为2 ；则保留，不再拆为 1+1 。
最差：1。若最后一段绳子长度为1 ；则应把一份3+1替换为 2+2，因为 2×2>3×1。

算法流程：

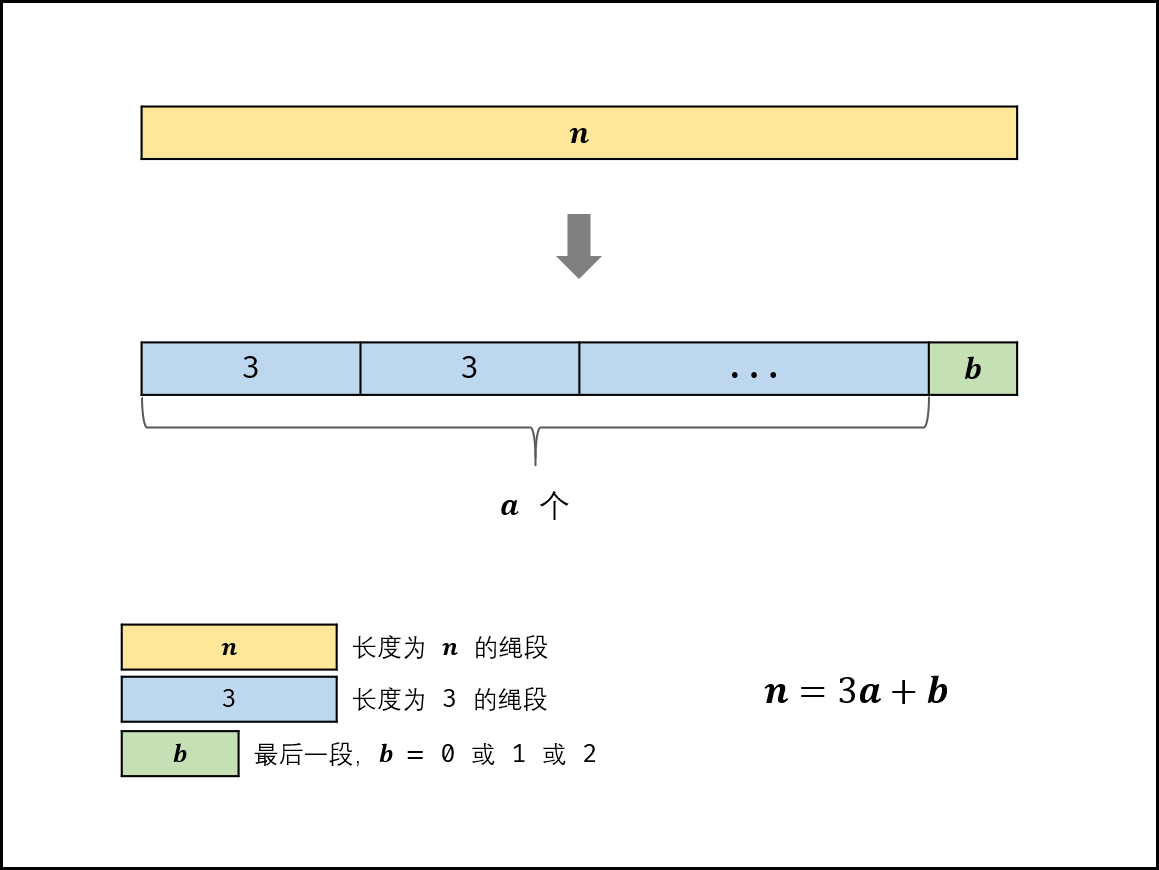
当n≤3时，按照规则应不切分，但由于题目要求必须剪成m>1段，因此必须剪出一段长度为1的绳子，即返回n−1。

当n>3时，求n除以 3的整数部分a和余数部分b （即 n=3a+b ），并分为以下三种情况（设求余操作符号为 "⊙" ）：

当 b=0时，直接返回 3a⊙1000000007；
当 b=1时，要将一个 1+3转换为 2+2，因此返回 (3a−1×4)⊙1000000007；
当 b=2时，返回 (3a×2)⊙1000000007。

大数求余解法：

大数越界：当a增大时，最后返回的3a大小以指数级别增长，可能超出int32 甚至int64 的取值范围，导致返回值错误。
大数求余问题：在仅使用int32 类型存储的前提下，正确计算xa对p求余（即 xa⊙p）的值。
解决方案：循环求余、快速幂求余，其中后者的时间复杂度更低，两种方法均基于以下求余运算规则推出：(xy)⊙p=[(x⊙p)(y⊙p)]⊙p

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n - 1;
        int b = n % 3, p = 1000000007;
        long rem = 1, x = 3;
        for(int a = n / 3 - 1; a > 0; a /= 2) {
            if(a % 2 == 1) rem = (rem * x) % p;
            x = (x * x) % p;
        }
        if(b == 0) return (int)(rem * 3 % p);
        if(b == 1) return (int)(rem * 4 % p);
        return (int)(rem * 6 % p);
    }
}