CNN中的Layers
除了正向传播计算loss,反向传播更新parameters,我们还需要知道参数是如何计算的,这个很重要。
我们这里介绍几个在deep learning中经常用到的几个层,dense layer(全连接层),convolutional layer(卷积层),pooling layer(池化层)。
可以参考:https://blog.csdn.net/qq_43369406/article/details/127134277
dense layer
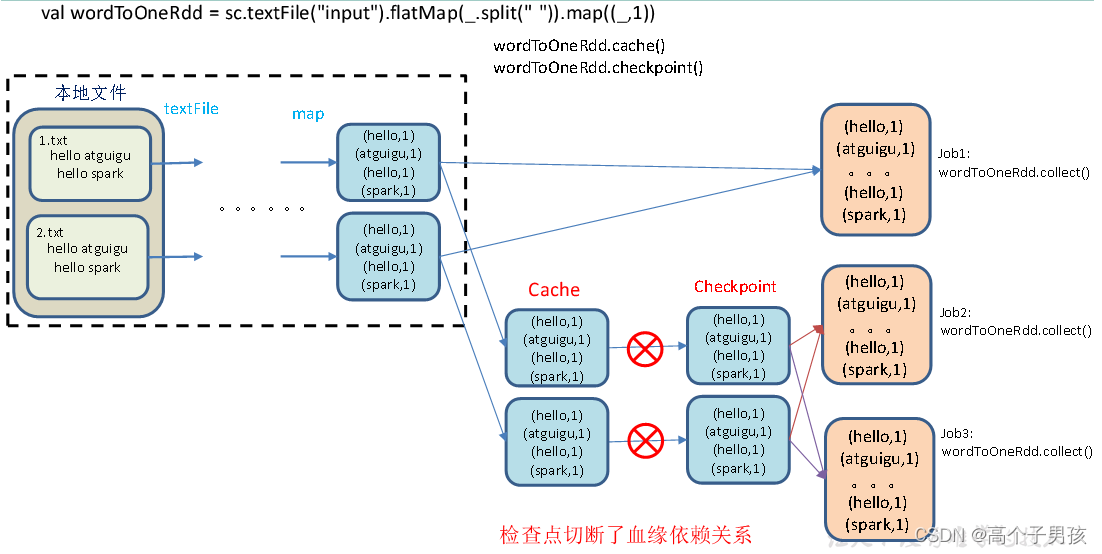
在全连接层中,我们只会关注所需要的参数的数量,这里的参数是指layer1到layer2上面连接的线上的权重值+1个bias(可以参考吴恩达机器学习)。例如下图的input layer到hidden layer1他们所需要的参数数量为(8+1)*9=81个参数。
convolutional layer
卷积层的主要作用是做特征提取。我们先介绍几个卷积层的特性,卷积层的计算方式,再主要介绍卷积后输出特征矩阵大小以及卷积层参数个数。
卷积层具有如下几个特性:
- 卷积层具有局部感知机制和权值共享。其中权值共享机制使得每一层卷积所需要的参数大大小于全连接层所需要的参数。
- 卷积核的channel(深度/维数)与输入特征矩阵的channel相同。
- 输出特征矩阵的channel(深度/维数)与卷积核的个数相同。
卷积层的计算方式如下所示,它采用的是矩阵点乘的方式,即对应元素相乘再相加的方式进行,再将所得值写在矩阵中间元素的位置。
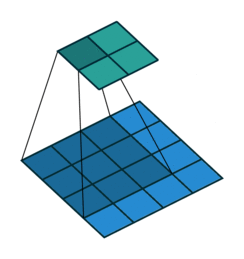
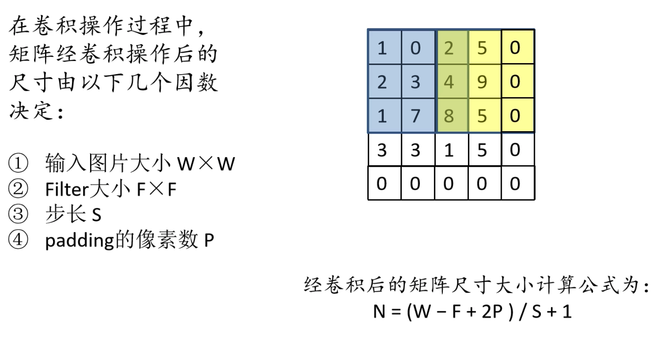
卷积后输出特征矩阵的深度等于卷积核的个数,输出特征矩阵的大小则有如下公式计算:
o u t p u t s i z e = ( i n p u t s i z e − f i l t e r s i z e + 2 ∗ p a d d i n g ) / s t r i d e + 1 outputsize=(inputsize-filtersize+2*padding)/stride+1 outputsize=(inputsize−filtersize+2∗padding)/stride+1
参数个数计算公式如下,其中1是bias:
n u m b e r = ( f i l t e r s i z e ∗ f i l t e r s i z e ∗ f i l t e t c h a n n e l + 1 ) ∗ f i l t e r n u m b e r number=(filtersize*filtersize*filtetchannel+1)*filternumber number=(filtersize∗filtersize∗filtetchannel+1)∗filternumber
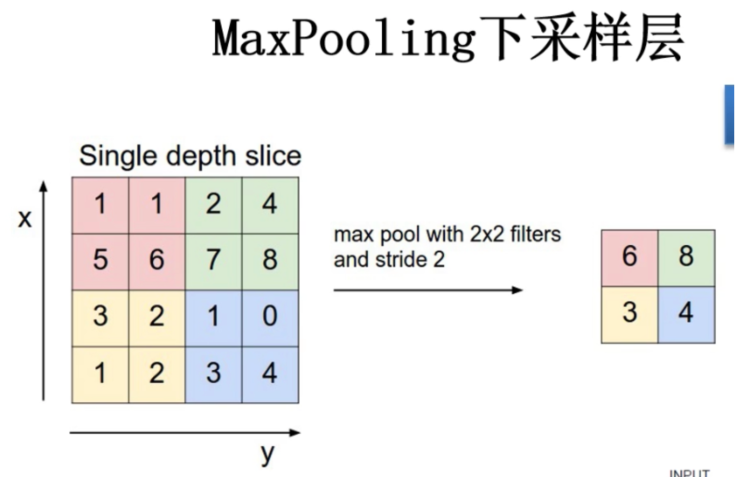
pooling layer
池化层没有参数。
Transposed convolution转置卷积
转置卷积又被称为transposed convolution、deconvolution,他的主要作用是upsampling 上采样,常见的上采样方法还有bilinear interpolation双线性插值。转置卷积的主要步骤为填充后再卷积,结果上说:将输出特征矩阵大小大于输入特征矩阵大小:
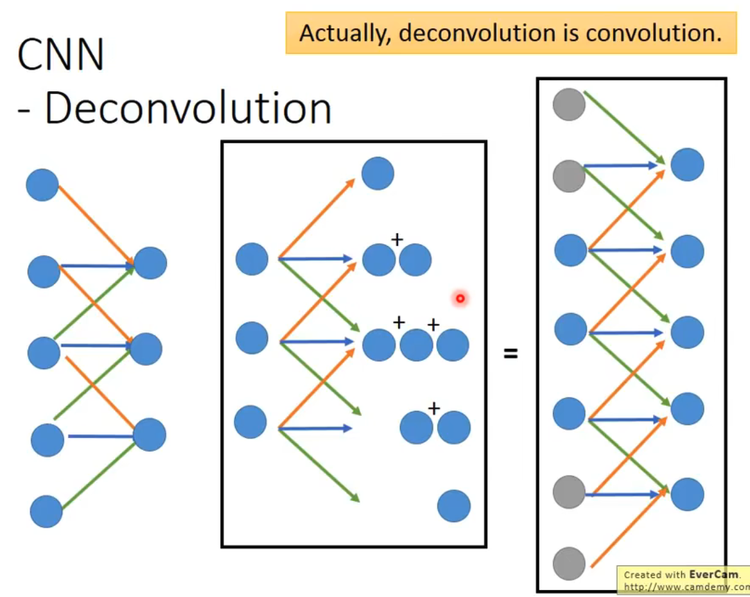
转置卷积也是卷积,主要完成两个操作:
- 填充
在输入特征矩阵的元素间填充stride-1行0和stride-1列0;在输入特征矩阵的元素四周填充kernelSize-padding-1行0和kernelSize-padding -1列0。将inputSize变为inputSize’案例如下(只需要看前两步,公式忽略):

- 将卷积核参数做上下、左右翻转(这里指的是将encoder时候的卷积核中参数旋转180度得到deconder时候的卷积核参数,不需要训练得到参数,而是通过将encoder时候训练的权重共享得到。ps:1. 转置矩阵是沿着y=-x轴对称(行列互换) 2. 这个卷积核180度旋转类似于反向传播时卷积核旋转180度。)
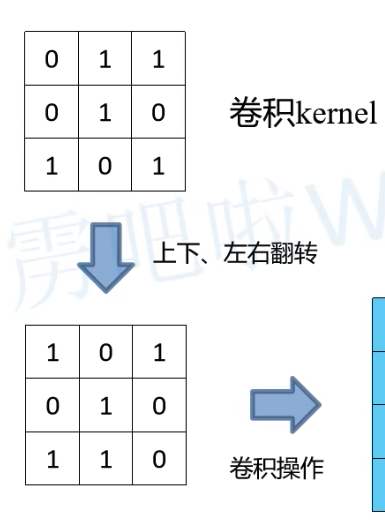
- 做正常卷积操作,其中paddinng=0,stride=1
o u t p u t S i z e = ( i n p u t S i z e ′ − k e r n e l S i z e + 2 ∗ p a d d i n g ) / s t r i d e + 1 outputSize = (inputSize'-{kernelSize}+2*padding)/stride+1 outputSize=(inputSize′−kernelSize+2∗padding)/stride+1
参考链接
- 转置卷积
https://www.bilibili.com/video/BV1mh411J7U4
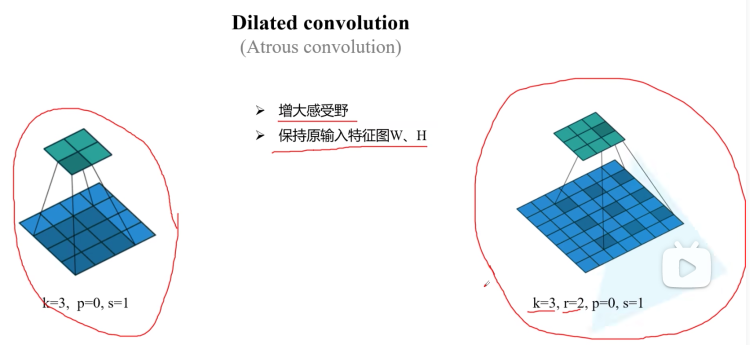
Dilated convolution空洞卷积
在语义分割中尽量不要下采样过大(例如VGG下采样了32倍),因为若下采样倍率过大,则在decoder的时候可能还原不回来。
dilated Conv又叫空洞卷积或者膨胀卷积。它的出现在于替代pooling层,即增大感受野的同时使得保持原输入特征图的高和宽不变(pooling层会使得特征图的高宽变小,例如VGG就缩小了32倍,会丢失很多信息,例如小目标的信息)。
但是在使用空洞卷积的时候会碰到例如gridding effect的问题,gridding effect即指的是在卷积的过程中,并不会用到所有像素信息,例如下图中白色部分的像素信息就没有使用到。
膨胀系数r=2,2,2
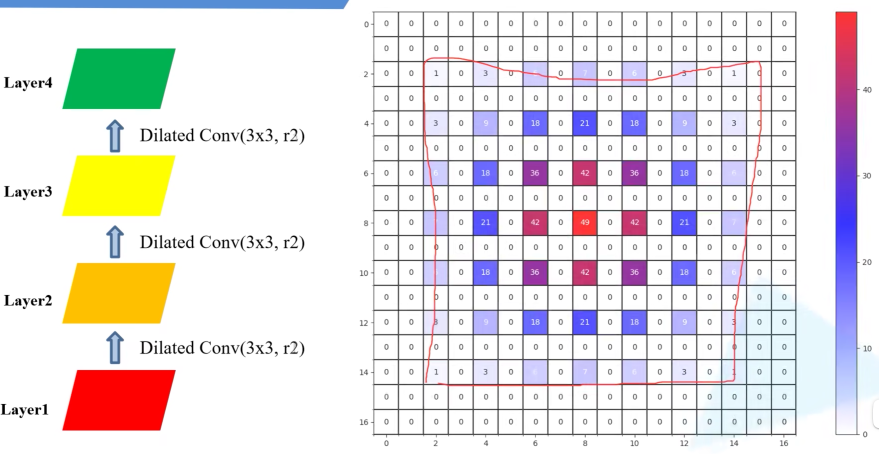
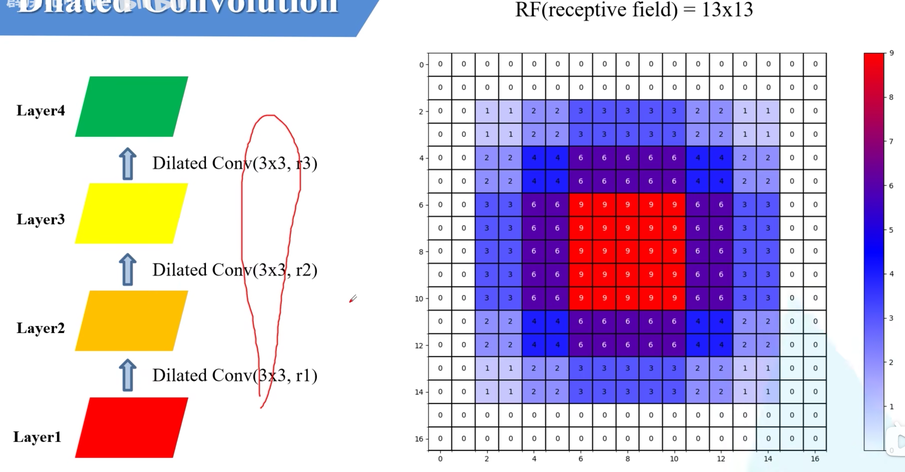
膨胀系数r=1,2,3
膨胀系数r=1,1,1
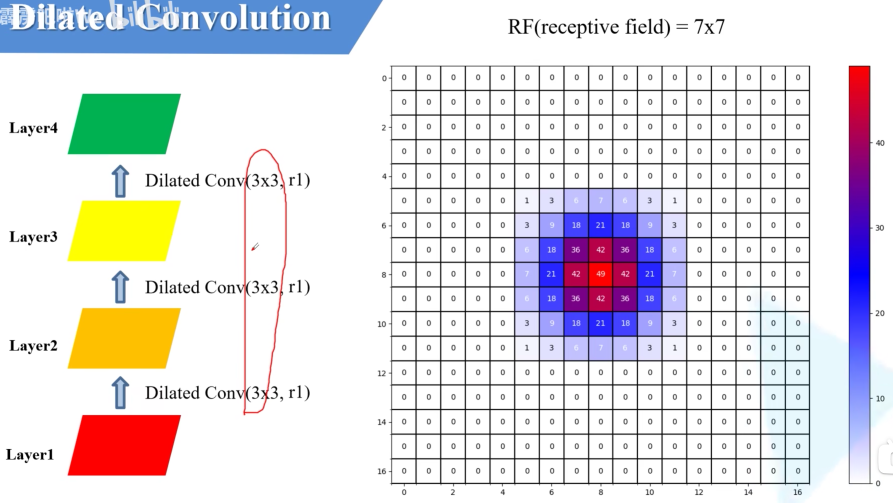
通过上述三组图,我们能够发现采用不同的膨胀系数,最终我们得到的receptive field(rf)感受野是不同的。我们需求则是:在保证不存在gridding effect的前提下,使得receptive field尽量大。根据这种需求我们提出了膨胀系数的设计准则:Hybrid Dilated Convolution(HDC)。
HDC的公式计算如下,只要满足 M 2 ≤ K M_2\le K M2≤K便可:

同时作者还提出了两个建议:建议将膨胀系数设置为锯齿结构(1,2,3,1,2,3);建议公约数不大于1;第1个膨胀系数为r=1。
参考链接:https://www.bilibili.com/video/BV1Bf4y1g7j8