二叉排序树的概念

单纯的二叉树存储数据没有太大的作用。

搜索二叉树作用很大。

搜索二叉树的一般都是用来查找。也可以用来排序，所以也叫做二叉排序树。
叫做二叉排序树的原因是因为他中序遍历是有序的。
因为中序的任何一颗子树，都要先走左子树，根，再走右子树。

搜索树因为数据不能冗余，所以也可以用来在插入的时候去重。

因为左子树<根<右子树，所以走中序出来，就是排序好的结果。

搜索二叉树要满足：
任意一颗子树都要满足，左子树的值小于根，右子树的值大于根。

优点：查找速度非常快。查找一个值，最多查找高度次，但是它的查找速度是O(n)。因为它有可能是单边树。所以后面会有一个平衡搜索二叉树，不如AVL树，红黑树。

但是我们要从搜索二叉树学起。

模拟二叉搜索树

搜索树的模板参数喜欢用k。k表示关键词的意思，因为喜欢搜索。

定义节点类

需要先定一个节点类。

template<class K>
struct BSTNode
{

	BSTNode<K>* _pLeft;
	BSTNode<K>* _pRight;

	K _key;
};

然后开始写二叉树的增删查改。

insert非递归

原则上插入不能有相同的数据插入。

搜索二叉树的插入顺序会影响效率。一般有序的话会影响。
为了能够找到cur的上一个结点，所以需要再定义个parent的节点。

template <class K>
class BSTree
{
	typedef BSTreeNode Node;//名字优化
public:
	bool Insert(const K& key)
	{
		//如果根节点为空
		if (_root == nullptr)
		{
			//new的时候直接可以填值。
			_root = new Node(key);

			return bool;
		}
		//否则开始
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			//如果在左边
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;

			}
			//如果在右边
			else if(key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			//不允许数据冗余
			else
			{
				return false;
			}
		}
		//循环结束,new一个空间.
		cur = new Node(key);
		//不知道链接到父亲的左边和右边。
		//这时候就需要再比较一次
		if (key > parent->_key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		return true;
	}
private:
	Node* _root = nullptr;//根节点
};

C++的根节点是私有的，封装了。所以没办法访问。
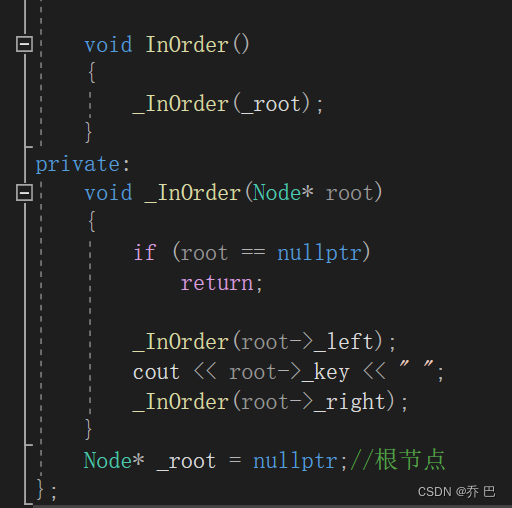
可以提供函数。也可以套一层。用_InOrder。
然后把_InOrder函数设为私有。

这样就不用传参了。
在这里插入图片描述

Find

查找值更简单。

   bool Find(const K& key)
    {
        Node* cur = _root;
        while(cur)
        {
            if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}

        }

        return false;
    }

erase(重点)

搜索树前面的问题都不算问题，最大的问题在于删除数据。删除数据是一个非常麻烦的事情。

1.删叶子节点最好删。
2.删只有一个孩子的也挺好删。只有一个孩子的话，托付给父亲就行，和Linux的托孤有点相似。

总结：没有孩子或者只有一个孩子的时候可以直接删除。
3.不好删的是：
假如有两个孩子则不好删。
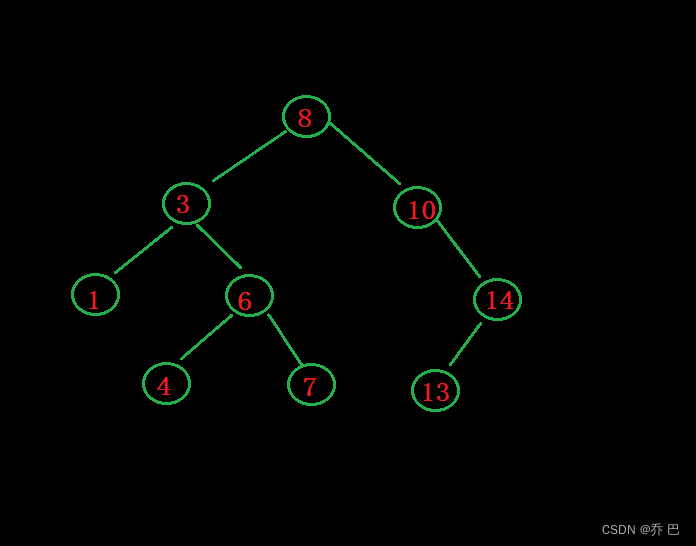
在这里插入图片描述

比如删除3。3有两个孩子。3的父亲8管不了两个孩子，因为8右子树也有孩子。

这时候需要用替换法删除。
替换法删除：

找谁替换呢？
找左子树的最大值结点。或者右子树的最小值结点。
为什么？
因为一棵搜索二叉树，最左边就是最小的值。最右边是最大的值。

关键理解：左子树的最大值结点做父亲可以满足比左子树的任意一个结点的值都大，同时随便拿出左子树的任意一个结点都比右子树小。

理解了上面的。有人找出了规律。
重点：
分三种情况
1.假如删除的节点的左子树为空(包括两个节点都为空的情况)。
2.假如删除的节点的右子树为空。(要注意假如是根节点的情况)
3.假如删除的节点的左右子树都不为空(替换法删除)。

具体遇到的bug需要根据实际图来解决。上面的三种情况只是个大概。

//非递归删除erase
	   bool Erase(const K& key)
    {
        Node* parent = nullptr;
        Node* cur = _root;
        while(cur)
        {
            if(key > cur->_key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if(key < cur->_key)  
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                //一个孩子 假如 左为空
                if(cur->_left == nullptr)
                {
                    if(cur == _root)
                    {
                        _root = cur->_right;
                    }

                    else{
                        if(cur == parent->_left)
                        {
                            parent->_left = cur->_right;
                        }
                        else
                        {
                            parent->_right = cur->_right;
                        }
                    }
                    delete cur;
                }
                //假如右为空
                else if(cur->_right == nullptr)
                {
                    if(cur == _root)
                    {
                        _root = cur->_left;
                    }

                    else{
                        if(cur == parent->_left)
                        {
                            parent->_left =  cur->_left;
                        }
                        else{
                            parent->_right = cur->_left;
                        }
                    }

                    delete cur;
                }

                //两个孩子都不为空
                else
                {
                    //右子树最小节点替代
                    Node* minParent = cur;
                    Node* minRight = cur->_right;
                    while(minRight->_left)
                    {
                        minParent = minRight;
                        minRight = minRight->_left;
                    }

                    swap(minRight->_key, cur->_key);

                    if(minParent->_left == minRight)
                    {
                        minParent->_left = 	minRight->_right;
                    }
                    else
                    {
                        minParent->_right = minRight->_right;
                    }

                    delete minRight;
                }

                return true;
            }
        }

        return false;
    }

析构函数

因为没有参数，无法调用析构函数递归，所以需要套一层进行递归。

private:
void DestortTree(Node* root)
{
	if(root == nullptr)
	return;
	DestoryTree(root->_left);
	DestoryTree(root->_right);
	delete root;
}
public:
~BSTree()
{
	DestoryTree(_root);
	_root = nullptr;
}

拷贝构造(深拷贝)

注意：只要有了拷贝构造就不会再生成默认的构造函数了，所以为了写拷贝构造函数，需要先写一个构造函数。
这时候就要显式写一个构造函数。或者可以用C++11的关键字default来强制生成默认构造

BSTree() = default;

假如我们不写拷贝构造函数，会默认生成构造函数进行浅拷贝。
为了保证树的形状，只能用前序遍历(根左子树右子树)递归拷贝。

private:
Node* CopyTree(Node* root)
{
	if(root == nullptr)
		return nullptr;
		
	Node* copyNode = new Node(root->key);
	copyNode->_left = CopyTree(root->_left);
	copyNode->_right = CopyTree(root->_right);
	
	return copyNode;
}
public:
BSTree(const BSTree<K>&  t)
{
	_root = CopyTree(t._root);
}

赋值构造

// t1 = t2

BSTree<K>& operator=(BSTree<K> t)
{
	swap(_root, t._root);
	return *this;
}

递归

FindR

返回下表的原因是因为要修改，但是这个树不需要修改，修改会破坏掉结构。所以返回bool值就ok。

C++类只要走递归一般都要套一层。不套一层一般都无法走递归。

InsertR

    bool InsertR(const K& key)
    {
        return _InsertR(_root, key);
    }

 bool _InsertR(Node*& root, const K& key)
    {
        if(root == nullptr)
        {
            root = new Node(key);
            return true;
        }

        if(root->_key < key)
            return _InsertR(root->_right, key);
        else if(root->_key > key)
            return _InsertR(root->_left, key);
        else
            return false;
    }