《机器学习》- 习题 - 第一章
文章目录
- 《机器学习》- 习题 - 第一章
- 一、示例-计算表1.1中的版本空间
- 二、习题 1 - 计算题目中的版本空间
- 三、单个合取式&析合范式的概念
- 四、习题 2 - 计算题目中假设空间的规模大小
一、示例-计算表1.1中的版本空间
首先从概念上理解版本空间的定义;
版本空间: 从
假设空间删除掉 与 正例不一致 和与 反例一致 的假设后,剩余的假设所组成的集合。它可以看成是对正例的最大泛化。
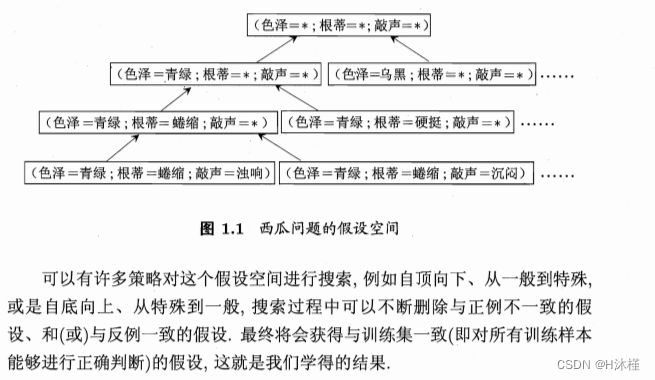
下图是书中的表1.1 西瓜数据集:

表1.1的训练数据集对应的假设空间如下:一共有49种 ;
“色泽” “根蒂” “敲声” 分别有 2、3、3种可能取值;则 面临的假设空间规模大小为 3 ∗ 4 ∗ 4 + 1 = 49 3 * 4 * 4 + 1 = 49 3∗4∗4+1=49 ;
将假设都列出来如下,为了便于理解,将不同的类型用分割线做了划分;
1 色泽=*,根蒂=*,敲声=*
2 色泽=青绿,根蒂=*,敲声=*
3 色泽=乌黑,根蒂=*,敲声=*
4 色泽=*,根蒂=蜷缩,敲声=*
5 色泽=*,根蒂=硬挺,敲声=*
6 色泽=*,根蒂=稍蜷,敲声=*
7 色泽=*,根蒂=*,敲声=浊响
8 色泽=*,根蒂=*,敲声=清脆
9 色泽=*,根蒂=*,敲声=沉闷
10 色泽=青绿,根蒂=蜷缩,敲声=*
11 色泽=青绿,根蒂=硬挺,敲声=*
12 色泽=青绿,根蒂=稍蜷,敲声=*
13 色泽=乌黑,根蒂=蜷缩,敲声=*
14 色泽=乌黑,根蒂=硬挺,敲声=*
15 色泽=乌黑,根蒂=稍蜷,敲声=*
16 色泽=青绿,根蒂=*,敲声=浊响
17 色泽=青绿,根蒂=*,敲声=清脆
18 色泽=青绿,根蒂=*,敲声=沉闷
19 色泽=乌黑,根蒂=*,敲声=浊响
20 色泽=乌黑,根蒂=*,敲声=清脆
21 色泽=乌黑,根蒂=*,敲声=沉闷
22 色泽=*,根蒂=蜷缩,敲声=浊响
23 色泽=*,根蒂=蜷缩,敲声=清脆
24 色泽=*,根蒂=蜷缩,敲声=沉闷
25 色泽=*,根蒂=硬挺,敲声=浊响
26 色泽=*,根蒂=硬挺,敲声=清脆
27 色泽=*,根蒂=硬挺,敲声=沉闷
28 色泽=*,根蒂=稍蜷,敲声=浊响
29 色泽=*,根蒂=稍蜷,敲声=清脆
30 色泽=*,根蒂=稍蜷,敲声=沉闷
31 色泽=青绿,根蒂=蜷缩,敲声=浊响
32 色泽=青绿,根蒂=蜷缩,敲声=清脆
33 色泽=青绿,根蒂=蜷缩,敲声=沉闷
34 色泽=青绿,根蒂=硬挺,敲声=浊响
35 色泽=青绿,根蒂=硬挺,敲声=清脆
36 色泽=青绿,根蒂=硬挺,敲声=沉闷
37 色泽=青绿,根蒂=稍蜷,敲声=浊响
38 色泽=青绿,根蒂=稍蜷,敲声=清脆
39 色泽=青绿,根蒂=稍蜷,敲声=沉闷
40 色泽=乌黑,根蒂=蜷缩,敲声=浊响
41 色泽=乌黑,根蒂=蜷缩,敲声=清脆
42 色泽=乌黑,根蒂=蜷缩,敲声=沉闷
43 色泽=乌黑,根蒂=硬挺,敲声=浊响
44 色泽=乌黑,根蒂=硬挺,敲声=清脆
45 色泽=乌黑,根蒂=硬挺,敲声=沉闷
46 色泽=乌黑,根蒂=稍蜷,敲声=浊响
47 色泽=乌黑,根蒂=稍蜷,敲声=清脆
48 色泽=乌黑,根蒂=稍蜷,敲声=沉闷
49 ∅ \varnothing ∅
按照上述过程进行学习:[ 删除 与正例不一致 与反例一致 的 假设 ]
对于编号为 1 的 样例来说:
(1,(色泽=青绿、根蒂=蜷缩、敲声=浊响),好瓜)
可以删除假设空间中的3、5、6、8、9、11-15、17-21、23-30、32-49 ;
对于编号为 2 的 样例来说:
(2,(色泽=乌黑、根蒂=蜷缩、敲声=浊响),好瓜)
可以删除剩余假设空间中的2、10、16、31 ;
对于编号为 3 的 样例来说:
(3,(色泽=青绿、根蒂=硬挺、敲声=清脆),坏瓜)
可以删除剩余假设空间中的 1 ;
对于编号为 4 的 样例来说:
(4,(色泽=乌黑、根蒂=稍蜷、敲声=沉闷),坏瓜)
剩余假设空间中无可删除的假设;
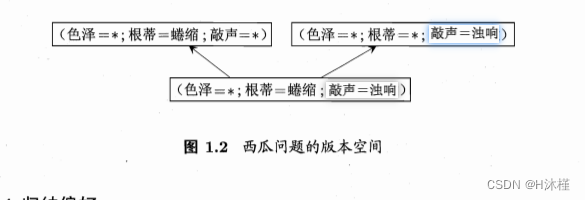
学习过后剩余的假设为:
4 色泽=*,根蒂=蜷缩,敲声=*
7 色泽=*,根蒂=*,敲声=浊响
22 色泽=*,根蒂=蜷缩,敲声=浊响
这就是最后的 “ 假设集合 ”,也就是 “ 版本空间 ” 。
二、习题 1 - 计算题目中的版本空间

习题1. 在表1.1 中 若只包含编号为1和4的两个样例,试给出相应的版本空间。
在上文一中示例的基础上,分析习题1中的问题:
按照上文一中示例进行学习:[ 删除 与正例不一致 与反例一致 的 假设 ]
对于编号为 1 的 样例来说:
(1,(色泽=青绿、根蒂=蜷缩、敲声=浊响),好瓜)
可以删除假设空间中的3、5、6、8、9、11-15、17-21、23-30、32-49 ;
对于编号为 4 的 样例来说:
(4,(色泽=乌黑、根蒂=稍蜷、敲声=沉闷),坏瓜)
剩余假设空间中的 1 ;
学习过后剩余的假设为:
剩下的假设有为:2、4、7、10、16、22、31 ;
2 色泽=青绿,根蒂=*,敲声=*
4 色泽=*,根蒂=蜷缩,敲声=*
7 色泽=*,根蒂=*,敲声=浊响
10 色泽=青绿,根蒂=蜷缩,敲声=*
16 色泽=青绿,根蒂=*,敲声=浊响
22 色泽=*,根蒂=蜷缩,敲声=浊响
31 色泽=青绿,根蒂=蜷缩,敲声=浊响
这就是最后的 “ 假设集合 ”,也就是 “ 版本空间 ” 。
三、单个合取式&析合范式的概念
析合范式(disjunctive normal form) 亦称 析取范式一种析取式。是若干简单合取式的析取式。(在《离散数学》这门课程中有学到过这个概念。)
析取范式是一种逻辑表达式,它包含两个子句,它们之间用"或"连接。
析取范式的典型形式是"P 或 Q",其中P和Q都可以是真实的或不真实的声明,
而该范式的结果将取决于P或Q或两者 都是真实的。
而合取范式则是另一种逻辑表达式,它包含两个子句,它们之间用“且”连接。
合取范式的典型形式是"P 且 Q",其中P和Q都可以是真实的或不真实的声明,而该范式的结果将取决于P和Q 都是真实的。
首先要明白 简单析取式 和 简单合取式 的定义。
定义:我们将命题变项及其否定统称作 文字 \red{文字} 文字。
简单析取式 \red{简单析取式} 简单析取式是仅由有限个文字构成的析取式。
简单合取式 \red{简单合取式} 简单合取式简单合取式是仅由有限个文字构成的合取式。
注意:一个简单文字既是简单析取式,又是简单合取式。
例如:
- p , ¬ q p , ¬q p,¬q既是一个简单析取式,又是一个简单合取式
- p ∨ ¬ q , p ∨ r p \vee¬q , p \vee r p∨¬q,p∨r 均是有两个文字的简单析取式
- p ∧ q ∧ r , ¬ p ∧ q ∧ ¬ q p \wedge q \wedge r , ¬ p \wedge q \wedge ¬q p∧q∧r,¬p∧q∧¬q 均是有三个文字的简单合取式
定义:
- 由有限个 简单合取式 \red{简单合取式} 简单合取式构成的 析取式 \red{析取式} 析取式被称为 析取范式 \red{析取范式} 析取范式.
- 由有限个 简单析取式 \red{简单析取式} 简单析取式构成的 合取式 \red{合取式} 合取式被称为 合取范式 \red{合取范式} 合取范式.
- 析取范式与合取范式统称为 范式 \red{范式} 范式.

性质:
一个文字既是一个析取范式又是一个合取范式
一个析取范式为矛盾式,当且仅当它的每一个简单合取式都是矛盾式
一个合取范式是重言式,当且仅当它的每一个简单析取式都是重言式
范式存在定理 \red{范式存在定理} 范式存在定理:任一命题公式都存在着与之等值的析取范式与合取范式。

此处参考博客 第一章 命题逻辑 1.4 析取范式与合取范式
如下图中,分别为析取范式和合取范式的示例:


依照上述的步骤解题2:

解:
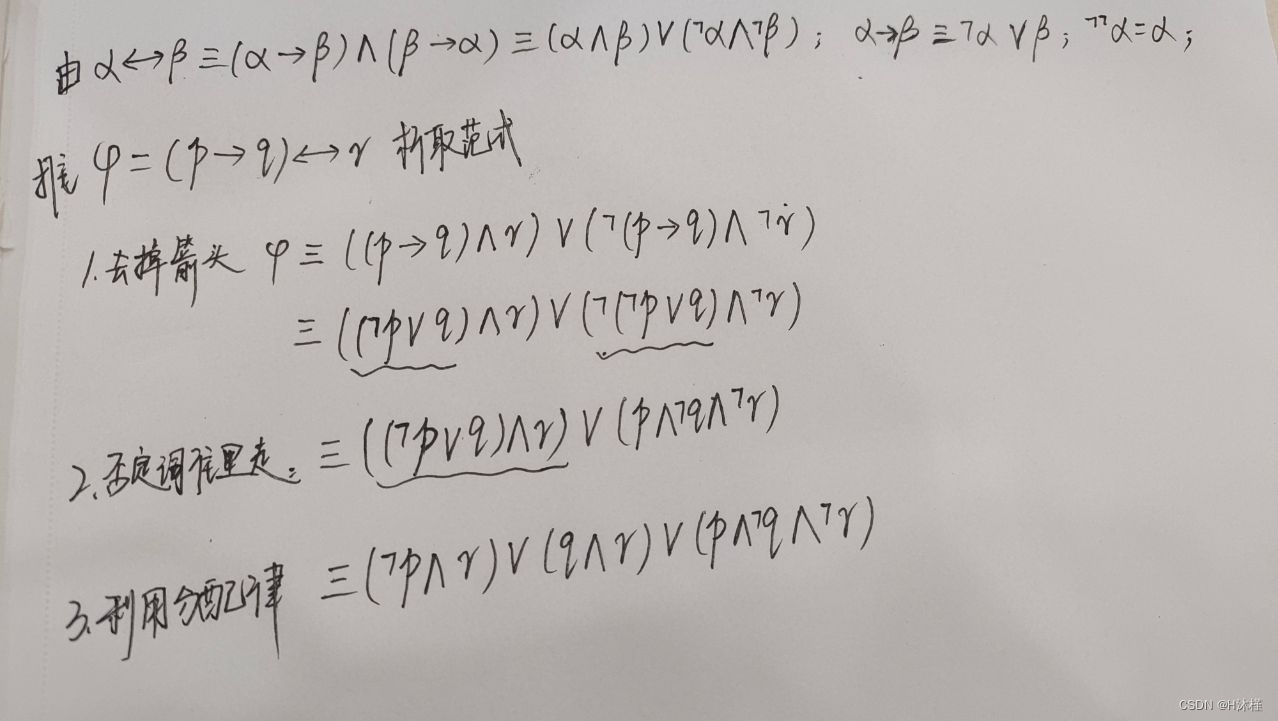
四、习题 2 - 计算题目中假设空间的规模大小

1.2 与使用单个合取式来进行假设表示相比,使 用 “析合范式”将使得假设空间具有更强的表示能力. 例如
好瓜
⇔
(
(
色泽
=
∗
)
∧
(
根蒂
=
蜷缩
)
∧
(
敲声
=
∗
)
)
∨
(
(
色泽
=
乌黑
)
∧
(
根蒂
=
∗
)
∧
(
敲声
=
沉闷
)
)
,
好瓜 \Leftrightarrow ((色 泽 = *) \land (根蒂= 蜷缩) \land (敲声= *)) \lor ((色泽=乌黑) \land (根蒂= *) \land (敲声= 沉闷)),
好瓜⇔((色泽=∗)∧(根蒂=蜷缩)∧(敲声=∗))∨((色泽=乌黑)∧(根蒂=∗)∧(敲声=沉闷)),
会 把 “
(
色泽
=
青绿
)
∧
(
根蒂
=
蜷缩
)
∧
(
敲声
=
清脆
)
(色泽=青绿) \land (根蒂= 蜷缩) \land (敲声=清脆)
(色泽=青绿)∧(根蒂=蜷缩)∧(敲声=清脆)”以 及 “
(
色泽
=
乌黑
)
∧
(
根蒂
=
硬挺
)
∧
(
敲声
=
沉闷
)
(色泽=乌黑) \land (根蒂= 硬挺) \land (敲声=沉闷)
(色泽=乌黑)∧(根蒂=硬挺)∧(敲声=沉闷)”都分类为 “好瓜”. 若使用最多包含
k
k
k 个 合取式的析合范式来表达表1.1西瓜分类问题的假设空间,试估算共有多少种可能的假设。
注:析合范式即多个合取式的析取.
提示:注意冗余情况,如 ( A = a ) V ( A = ∗ ) (A = a) V (A = *) (A=a)V(A=∗) 与 ( A = ∗ ) (A = *) (A=∗)等价.
由题1.1知,共有49种假设,其中:
全部不泛化 2 ∗ 3 ∗ 3 = 18 2 ∗ 3 ∗ 3 = 18 2∗3∗3=18种假设;
一个属性泛化: 2 ∗ 3 + 3 ∗ 3 + 2 ∗ 3 = 21 2 ∗ 3 + 3 ∗ 3 + 2 ∗ 3 = 21 2∗3+3∗3+2∗3=21 种假设;
两个属性泛化: 2 + 3 + 3 = 8 2 + 3 + 3 = 8 2+3+3=8 种假设;
三属性泛化:1种假设
空集:1种假设
不考虑空集,则有48种假设,所以k的最大值为48。
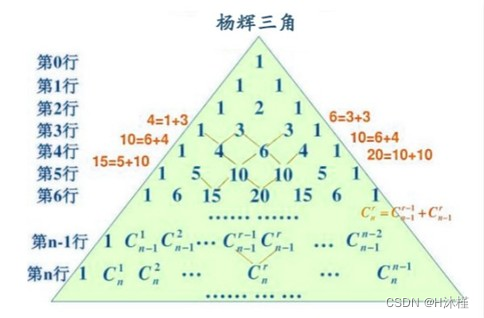
而组成的析合范式是这48种假设的排列组合,展开序列为(即杨辉三角【二项式系数在三角形中的一种几何排列】 的一排):

(
1
、
48
、
1128
、
…
、
1128
、
48
、
1
)
(1、48、1128、… 、1128、48、1)
(1、48、1128、…、1128、48、1)共49个数,
左边的1表示:一个假设都没选,右边的1表示:全部假设都被选。
如果 k = 48 k=48 k=48,就是说最多采用 48 48 48 种合取式来组成析合范式,排除一种都不选的情况,就是 2 48 − 1 2^{48} - 1 248−1种。( 2 48 2^{48} 248是根据二项式系数之和得的);
如果 0 < k < 48 0<k<48 0<k<48,那就把展开序列的前 k + 1 k+1 k+1(因为展开序列从 0 开始数)项全部加起来再减1 ;
如果指定了 k k k 的个数,那就是展开序列的第 k + 1 k+1 k+1(因为展开序列从 0 开始数)项的数 ;
但是,这个结果得去重才行,因为 泛化是对若干种假设的包含(包容),它本身不是某种假设。
把泛化的
∗
*
∗ 展开后,就是若干种具体的假设。如果此题采取
48
48
48,那么把
∗
*
∗ 展开后,假设集合中一定有重复,而且一种具体假设还不止重复一次。
此题应该采用18种具体假设来计算, 即:
2
18
−
1
2^{18} - 1
218−1