文章目录
- 什么是PCA(Principal Component Analysis)
- 协方差矩阵
- 什么是协方差
- 协方差矩阵
- 特征值与特征向量
- PCA降维
什么是PCA(Principal Component Analysis)
在机器学习中,PCA(Principal Component Analysis,主成分分析)是一种常用的降维方法。它可以将高维数据降至低维,同时保留数据的最重要的特征,从而方便后续的分析和处理。
PCA的基本思想是通过线性变换将原始数据投影到一个新的坐标系中,使得投影后的数据具有最大的方差。这样可以减少特征之间的冗余信息,从而达到降维的目的。
比方说有这样一组高维数据,它输出的图像1是这样的

对于我们来说,对高纬度数据进行分析,需要考虑的变量信息太多,所以我们就会考虑舍弃掉其中不太重要的信息,而保留能够反映数据特征信息,因此对于上面这个例子,我们可以选择一个合适的平面对原始数据进行投影,于是可以得到:

数据基本信息没有发生改变,但影响我们分析数据特征的高纬信息消失了,这样的一个过程就是PCA的实现过程。那么,具体来说,它的主要步骤包括:
- 对原始数据进行去均值化(即将数据中心化);
- 计算协方差矩阵(或者是相关系数矩阵);
- 对协方差矩阵进行特征值分解,得到特征向量和特征值;
- 将特征向量按照对应的特征值大小排序,选择前k个特征向量作为新的坐标轴;
- 将原始数据投影到新的坐标轴上,得到降维后的数据。
在PCA中,特征向量表示数据在新的坐标系中的方向,特征值表示数据在特征向量方向上的重要程度。因此,选择前k个特征向量可以保留数据最重要的特征,并且可以通过特征值来确定保留多少特征。
协方差矩阵
什么是协方差
协方差(Covariance)是描述两个变量之间关系的统计量,它反映了两个变量的联合变化程度。具体来说,协方差是指两个随机变量的离差积的期望值,其计算公式为:
C o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] Cov(X,Y) = E[(X-E(X))(Y-E(Y))] Cov(X,Y)=E[(X−E(X))(Y−E(Y))]
其中,X和Y分别为两个随机变量,E(X)和E(Y)分别为它们的期望值。X和Y的协方差越大,说明它们的联合变化程度越大,也就意味着它们之间存在一定的相关性。
协方差的符号表示两个变量的关系:
- 当协方差为正值时,说明两个变量正相关,即其中一个变量增大时,另一个变量也会增大;
- 当协方差为负值时,说明两个变量负相关,即其中一个变量增大时,另一个变量会减小;
- 当协方差为零时,说明两个变量不相关,即它们之间不存在线性相关关系。
因为在我以前的文章里已经有提到过协方差的概念,如果想更近一步了解协方差的同学,可以点击这里。
协方差矩阵
从协方差这个概念出发,我们可以通过计算不同特征的关联来获得一个名叫协方差矩阵。协方差矩阵是PCA(Principal Component Analysis)方法的重要组成部分,它描述了数据中不同特征之间的关系,可以用于进行特征提取和降维。
统计学的,对于一个包含m个样本和n个特征的数据集X,其协方差矩阵S的计算公式为:
S = 1 m − 1 ∑ i = 1 m ( x i − x ‾ ) T ( x i − x ‾ ) S = \frac{1}{m-1} \sum_{i=1}^{m} (x_i - \overline{x})^T (x_i - \overline{x}) S=m−11i=1∑m(xi−x)T(xi−x)
其中, x i x_i xi是第i个样本的特征向量, x ‾ \overline{x} x是所有样本的平均值。协方差矩阵的对角线上的元素是每个特征的方差,非对角线上的元素则表示不同特征之间的协方差。
例如,以鸢尾花的样本为例,该数据集有三种样本,每一种样本都有花瓣长宽、花萼长宽。

如果把数据绘制出来,并分别以其中两个属性组成一组散点图,那么就是上面这个样子。阅读的时候,只要看下三角行列就足够了。可以看出,有一部分特征之间存在高度重合,而另外一些特征存在比较清晰的边界。
因此,只要对上述散点图进行适当转换和计算,就能得到协方差矩阵(记住,中间斜线部分不是协方差,而是样本各特征的方差)。

然后我们可以从协方差矩阵进一步得到特征值和特征向量。
特征值与特征向量
特征值的计算需要使用到线性代数的知识。给定一个矩阵A,如果存在一个非零向量v和一个标量λ,满足以下关系:
A = λ ⋅ v \mathbf A = \lambda \cdot \mathbf v A=λ⋅v
则称向量 v \mathbf v v 是矩阵A的特征向量(eigenvector),对应的标量 λ \lambda λ 则是矩阵 A \mathbf A A 的特征值(eigenvalue)。特征向量代表了矩阵A的某种“拉伸”或“压缩”效果,特征值则代表了这种“拉伸”或“压缩”效果的大小。
在PCA中,我们通常会使用协方差矩阵的特征值和特征向量来选择新的特征空间。具体来说,协方差矩阵的特征向量代表了数据在原有特征空间中的主要方向,而特征值则代表了数据在这些方向上的“重要程度”。
通常,特征值和特征向量可以通过调用NumPy库中的eigvals函数或者SciPy库中的eig函数来计算。对于我们的鸢尾花,可以得到
特征值: [4.22824171,0.24267075, 0.0782095, 0.02383509]
特征向量1:[ 0.36138659,-0.65658877, -0.58202985, 0.31548719]
特征向量2:[-0.08452251, -0.73016143, 0.59791083, -0.3197231 ]
特征向量3: [ 0.85667061, 0.17337266, 0.07623608, -0.47983899]
特征向量4: [ 0.3582892, 0.07548102, 0.54583143, 0.75365743]]
PCA降维
对于上述结果,在进行PCA降维时,我们通常会根据协方差矩阵的特征值从大到小排序,然后选择前几个特征值所对应的特征向量作为新的特征空间。这里的“前几个”通常是根据总方差贡献率来决定的,例如我们可以选择保留总方差的90%、95%或99%等。
根据输出结果,协方差矩阵的特征值从大到小依次是:
4.22824171, 0.24267075, 0.0782095, 0.02383509
我们可以看到,第一个特征值(4.22824171)远大于其他三个特征值,因此我们可以选择只保留第一个特征向量所代表的方向作为新的特征空间,即进行一维降维。当然,我们也可以选择保留前两个特征向量作为新的二维特征空间,这样也可以很好地保留数据的主要信息。具体来说,如果我们选择保留前两个特征向量,那么我们应该选取第一个和第二个特征向量,即:
特征值:4.22824171, 0.24267075
特征向量:[0.36138659, -0.08452251], [-0.65658877, -0.73016143], [-0.58202985, 0.59791083], [0.31548719, -0.3197231]
我们可以看到,第一个特征向量的分量(0.36138659, -0.65658877, -0.58202985, 0.31548719)代表了数据在第一维上的主要方向,第二个特征向量的分量(-0.08452251, -0.73016143, 0.59791083, -0.3197231)代表了数据在第二维上的主要方向。因此,如果我们只保留这两个特征向量所代表的方向,就可以得到一个新的二维特征空间。
在PCA中,我们通常会将原始数据投影到新的特征空间上,以得到降维后的数据。具体来说,对于一个d维的数据样本,我们可以将它投影到前k个特征向量所代表的新特征空间上,得到一个k维的数据样本。
假设我们选择保留前两个特征向量,即将数据降到二维。那么我们可以将原始数据样本矩阵X乘以前两个特征向量的转置矩阵,得到一个新的二维数据样本矩阵X_pca:
# 鸢尾花的数据
iris = load_iris()
X = iris.data
y = iris.target
...
# 计算协方差矩阵
cov_matrix = np.cov(X.T)
...
# 计算协方差矩阵的特征值和特征向量
eigvals, eigvecs = np.linalg.eig(cov_matrix)
...
# 投影到新的二维空间中
X_pca = X.dot(eigvecs[:, :2])
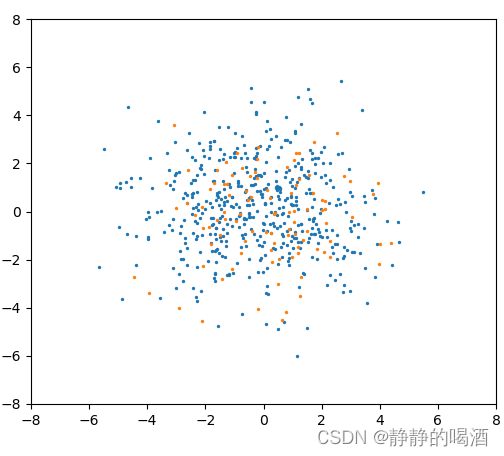
这里的eigvecs[:, :2]表示选取协方差矩阵的前两个特征向量,即投影到二维特征空间上。dot函数表示矩阵乘法。最终得到的X_pca矩阵中,每一行代表一个新的二维数据样本。
于是我们得到了PCA降维后的图片

图片来源:https://towardsdatascience.com/principal-component-analysis-pca-explained-visually-with-zero-math-1cbf392b9e7d ↩︎








![[ 云计算入门与实战 - AWS ] 在控制台创建 Amazon EC2 实例](https://img-blog.csdnimg.cn/20e9cf4402d94f6fa8245139a5c0b92a.png)