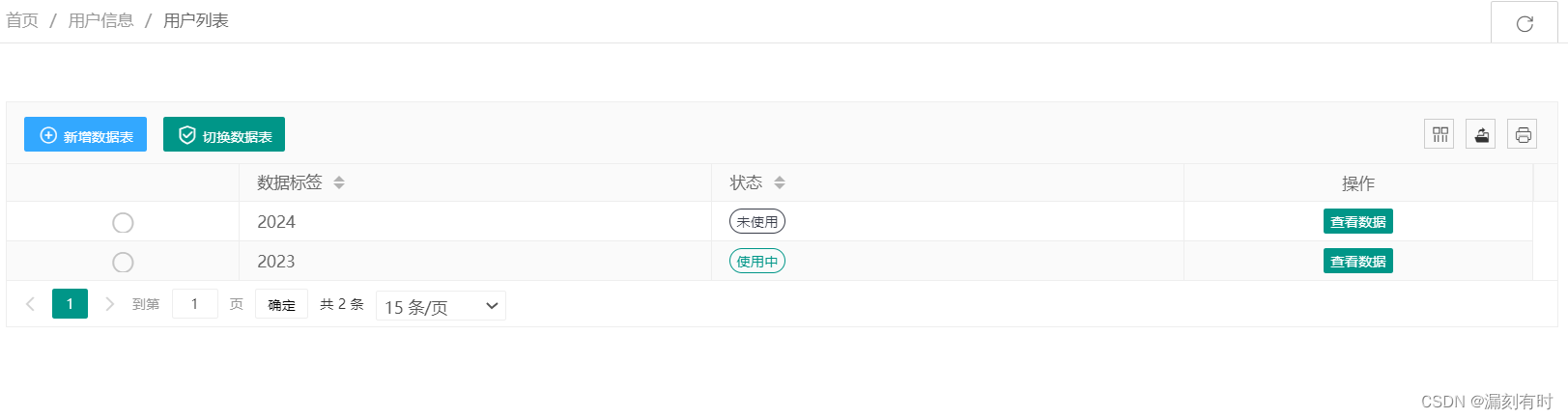
一、概述
1.图
图用来表示一些实体(entities)之间的关系(实体表示为点(node),关系表示为边(edge))。

关系分为有方向和无方向

2.数据的图表示
以图像文件为例,我们可以用邻接矩阵来表示一张图像。每个点表示一个像素点,若一个像素点有x个相邻像素,则可以用x条边来表示这个点的关系。

以文字序列为例,同样可以使用邻接矩阵来表示这句话。相邻的两个词之间有一条有向边相连接。

其次,原子序列/社交网络/知识图等都能表示为一个邻接矩阵。
3.任务类型
图层面的任务、顶点层面的任务、边层面的任务。分类的依据是任务需要对这一层面(如图、点、边)的属性进行学习和预测。
二、图和神经网络
1.图的数据结构
一张图包含:顶点的属性、边的属性、全局信息、连接性。其中顶点的属性、边的属性、全局信息均可表示为向量。而连接性不能以一般矩阵表示(需要做到属性与顺序无关)
以下图为例,可以如此表述

Nodes
[0,1,1,0,0,1,0,0]表示每个顶点的属性(标量/向量)
Edges
[2,1,1,1,2,1,1]表示每条边的属性(标量/向量)
Adjacency List #邻接列表
[[1,0],[2,0],[4,3],[6,2],[7,3],[7,4],[7,5]]长度=边数;第 i 个向量表示第 i 条边连接的哪些结点。
Global
0全局信息(标量/向量)
2.图神经网络(GNN)
GNN:对图上所有的属性(顶点、边、全局)进行的一个可以优化的变化(此变换能保持图的对称信息<即将顶点以另一种方法排序后结果不变>)。经过一个信息传递神经网络的输入输出都是一张图(会改变顶点和边的属性,但不会改变连接性)。
在输出图后,根据任务不同,分别对顶点向量、边向量和全局向量构造一个MLP(多层感知机)

在MLP后添加全连接层和激活函数即可得到预测值(所有的属性共用一个全连接层)
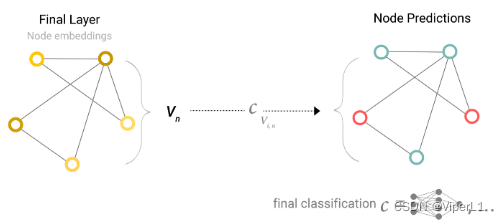
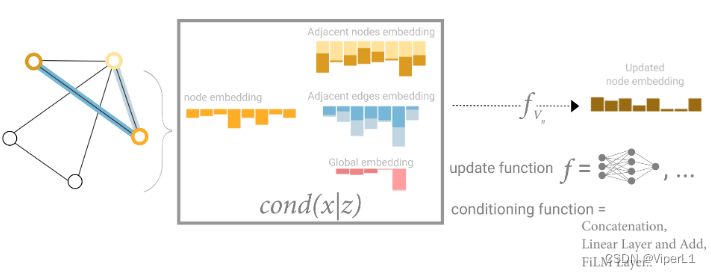
Pooling(汇聚):若需要预测顶点但没有顶点的向量,则可使用与该顶点连接的所有边的向量和全局向量进行叠加来代表该点的向量。
同理,缺少边向量或全局向量均可采用汇聚其他向量的方式来代替。

最简GNN结构如下:

将图输入GNN单元,分别对顶点向量、边向量、全局向量进行分别变换,得到一张图,在经过全连接层和激活函数得到预测结果;若缺失部分属性可以用其他属性的汇聚来代替。
3.汇聚在GNN中的作用
在最简GNN中,GNN模块不会对图的连接性进行改变,为了充分利用图的连接性。我们可以利用信息传递对GNN进行改进。
具体做法是将某个顶点和他的两个邻居顶点的向量加在一起形成一个汇聚向量,再将此汇聚向量送入MLP,最后再将其更新到下一层。

汇聚操作类似于在图片上进行卷积,与卷积最大的区别是,卷积核感受野内的元素是进行加权求和(卷积核权重x像素值),而汇聚的求和是不加权求和。
汇聚同样可以取最大值和平均值,类似于CNN中的MaxPooling和MeanPooking。

汇聚操作并不是单向的,在实际堆叠中我们可以将信息从顶点传递给边也可以再将其传递回去,全部完成后在进入MLP。传递顺序不同会影响最终结果(可以交替进行)。

若图像结合不够紧密导致一个结点的信息需要传递很远才能达到目标结点。我们可以设置一个Master Node(虚拟结点,设定其与图上所有点相连,标记为),当需要把顶点的信息汇聚给边的时候,可以将
的信息进行汇聚。
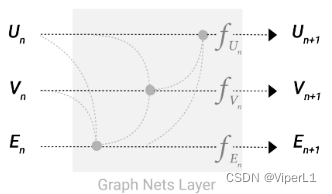
!!!经过上述处理,GNN可以使用顶点本身的向量进行预测,也可以使用和顶点相关的全部信息进行预测。称为“基于消息传递的图神经网络”
三、图的采样和batch
当网络层数较大时,前向传递梯度时必须将图进行采样(否则会占用过多内存)
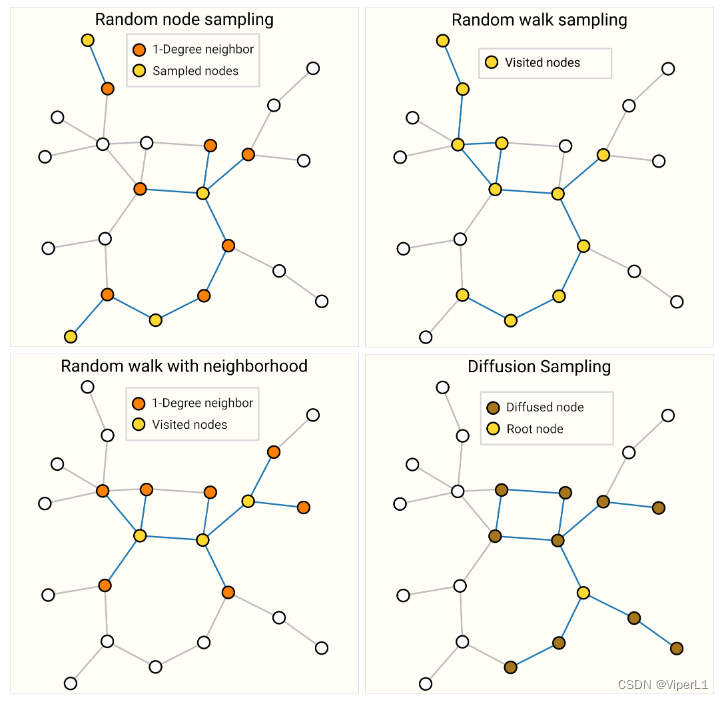
常见的采样方式如下:
①随机采样:随机选取一些点,并获取其最近的邻居;可以规定采样点的数量
②随机游走:从某个顶点开始,沿着图随机游走;可以规定游走的步数
③随机采样+随机游走
④宽度遍历:取一个点,将其1、2、3近邻进行一个k步的宽度遍历
四、假设问题
对于CNN而言,假设的是空间变换的不变性;对于RNN而言,假设的是时间的延续性;而对于GNN而言,假设是图的对称性(交换图的顺序不改变图的性质)
无、GNN相关技术
①GCN网络
GCN(graph convolutional networks)-->图卷积神经网络,即带有汇聚操作的图神经网络
假设GCN有k层,且每层使用宽度遍历检索目标点的3个邻居,其可以近似为k层3x3的卷积神经网络,子图可以近似为特征图。
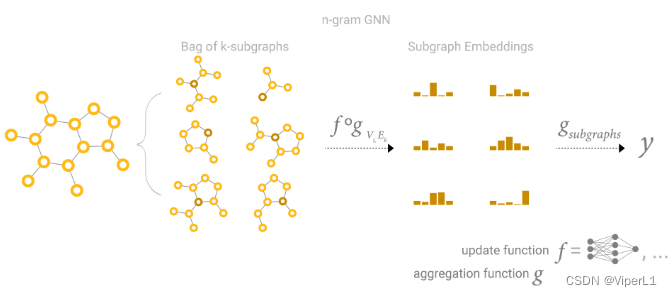
GCN在图上进行卷积等价于将邻接矩阵取出进行矩阵乘法。
②GAN网络
GAN(graph attention networks)--图注意力网络,GNN的汇聚操作是不带权重的求和,某些时候为了满足计算需要我们也可以对求和进行加权。不同于CNN的加权求和(CNN的权重与位置有关),因为要满足连接不变特性,GNN的加权求和必须保证与位置不敏感;一般而言可以采用注意力机制的做法--权重取决于两个顶点之间向量的关系。在Attenion后,我们将得到的权重与顶点进行点乘再求和即可。