【题目来源】
https://www.luogu.com.cn/problem/U91193
【问题描述】
在一个2^k * 2^k(k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格。现在用4种不同形状的 L型(占3小格)骨牌覆盖棋盘上除了特殊方格以外的所有方格,且各骨牌不能重叠。 步骤为:将棋盘一分为四,依次处理左上角,右上角,左下角,右下角,递归进行。严格按照这个顺序处理。
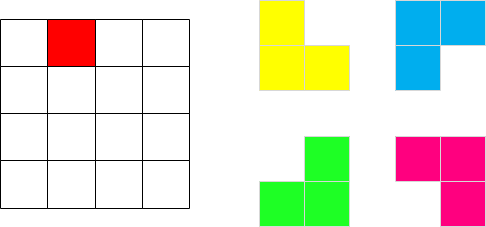
例如,一种用不同形状的 L型骨牌覆盖填充的策略如下图所示:

【输入格式 】
输入三个数k,x,y,分别表示棋盘大小,特殊方格位置。
【输出格式】
共2^k行,每行2^k个数,每辆个数中间空格隔开。
输出按照上述顺序所覆盖的棋盘。特殊方格用0表示,其他为骨牌编号。
【算法分析】
应用分治法求解棋盘覆盖问题的技巧在于如何划分棋盘,要求是使划分后的子棋盘的大小相同,从而将原来规模较大的棋盘覆盖问题分解为规模较小的棋盘覆盖问题。
其常用技巧是,当 时,将
的棋盘划分为4个
的子棋盘。由于原棋盘只有一个特殊方格,所以这样划分后,这4个子棋盘中只有一个子棋盘包含该特殊方格,其余3个子棋盘中没有特殊方格。然后,用一个L型骨盘覆盖这3个没有特殊方格的子棋盘的会合处,并将这三个子棋盘上被L型骨牌覆盖的方格标记为新的特殊方格。递归地使用这种分割方法,直至棋盘简化为
的棋盘,就结束递归。(注意:下图中的红色特殊方格,可以在其所在子棋盘的任意位置。下图只是示意需要选择的位置。)
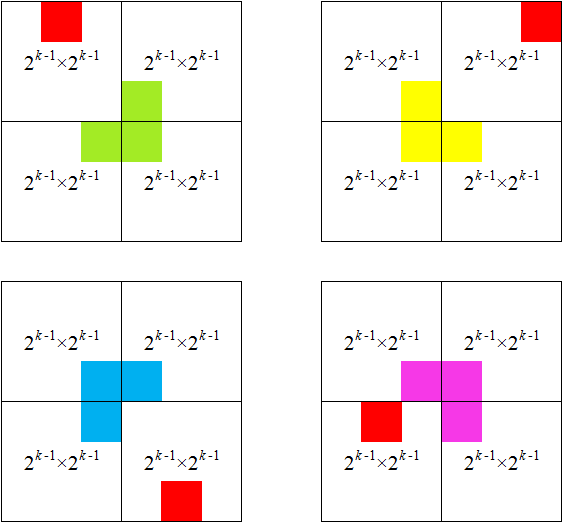
上图用语言表述为:
◆左上的子棋盘(若不存在特殊方格)----则将该子棋盘右下角的那个方格假设为特殊方格
◆右上的子棋盘(若不存在特殊方格)----则将该子棋盘左下角的那个方格假设为特殊方格
◆左下的子棋盘(若不存在特殊方格)----则将该子棋盘右上角的那个方格假设为特殊方格
◆右下的子棋盘(若不存在特殊方格)----则将该子棋盘左上角的那个方格假设为特殊方格
【数据范围】
说明/提示:k<=5
【算法代码】
#include <bits/stdc++.h>
using namespace std;
const int maxn=1005;
int ans[maxn][maxn];
int id;
void solve(int x1,int y1,int x2,int y2,int sz) {
if(sz==1) return;
int t=++id;
sz/=2;
int midx=x1+sz-1;
int midy=y1+sz-1;
if(x2<=midx && y2<=midy) { //特殊方格在左上部分,继续划分
solve(x1,y1,x2,y2,sz);
} else {
ans[midx][midy]=t; //不在左上,覆盖左上部分的右下角
solve(x1,y1,midx,midy,sz); //继续划分
}
if(x2<=midx && y2>midy) { //特殊方格在右上部分,继续划分
solve(x1,y1+sz,x2,y2,sz);
} else {
ans[midx][midy+1]=t; //不在右上,覆盖右上部分的左下角
solve(x1,y1+sz,midx,midy+1,sz); //继续划分
}
if(x2>midx && y2<=midy) { //特殊方格在左下部分,继续划分
solve(x1+sz,y1,x2,y2,sz);
} else {
ans[midx+1][midy]=t; //不在左下,覆盖左下部分的右上角
solve(x1+sz,y1,midx+1,midy,sz); //继续划分
}
if(x2>midx && y2>midy) { //特殊方格在右下部分,继续划分
solve(x1+sz,y1+sz,x2,y2,sz);
} else {
ans[midx+1][midy+1]=t; //不在右下,覆盖右下部分的左上角
solve(x1+sz,y1+sz,midx+1,midy+1,sz); //继续划分
}
}
int main() {
int k,x,y;
cin>>k>>x>>y;
int size=(1<<k);
solve(1,1,x,y,size);
for(int i=1; i<=size; i++)
for(int j=1; j<=size; j++) {
if(j==size) printf("%d\n",ans[i][j]);
else printf("%d ",ans[i][j]);
}
return 0;
}
/*
3
1 1
ans:
0 3 4 4 8 8 9 9
3 3 2 4 8 7 7 9
5 2 2 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21
*/
【参考文献】
https://blog.csdn.net/ljw_study_in_CSDN/article/details/106409784
https://www.codenong.com/cs105800665/
https://www.cnblogs.com/crx234/p/5988055.html
https://www.cnblogs.com/yanyu01/p/8734212.html
https://blog.csdn.net/scliu12345/article/details/102387130