1.熵
信息熵是消除不确定性所需信息量的度量。
信息熵就是信息的不确定程度，信息熵越小，信息越确定。
对象的信息熵是正比于它的概率的负对数的，也就是
I©=−log(pc)

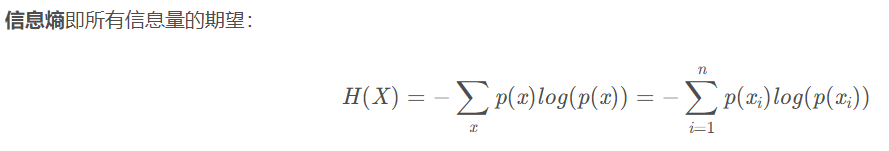
其中n为事件的所有可能性。
为什么使用交叉熵？在机器学习中，我们希望模型在训练数据上学到的预测数据分布与真实数据分布越相近越好，上面讲过了，用相对熵，但是为了简便计算使用交叉熵就可以了。
注：此处真实数据分布指的就是训练数据的分布(标注)。
以上信息来自博客为什么用交叉熵做损失函数讲得很清楚

2.线性规划
一个线性规划问题是一个线性函数最小化或最大化的问题，该线性函数服从一组有限个线性约束。
“线性编程”建议告诉计算机做线性的事情。 但这不是本课程标题中“编程”一词的含义。 在这种情况下，“编程”意味着“优化”：在集合中找到使函数值最大化的点。
线性规划是我知道的最酷的算法之一。线性规划用于在给定约束条件下最大限度地改善指定的指标。
下面是一个线性规划的例子：

详见线性规划简介
3.半监督自监督聚类打标签

半监督也有这个打伪标签的，多次迭代的过程。那么自监督和半监督的异同之处是什么？没什么太大区别。主要是计算聚类不需要标签啥的已知信息，所以自监督啥都不知道的情况下就可以找聚类中心。
实例：
Self-supervised Pseudo-labeling：
整个过程计算了两次聚类中心，第一次用输出的概率进行加权平均，然后用余弦距离加伪标签，然后用k-means聚类的方法再求一次聚类中心，再用余弦距离加伪标签，这样得到的伪标签较为准确。接着进行自监督，损失函数也是交叉熵损失函数。
这里是加权k-means聚类，之前知道的预测分类，使用余弦距离打标签。下图所示过程是论文“Do We Really Need to Access the Source Data? Source Hypothesis Transfer for Unsupervised Domain Adaptation”中的。

半监督：把没标注的数据先归到最近类，然后更新聚类中心，再把没标注的数据归类，迭代直到没有变化。

一下聚类摘自常用聚类算法
1.1聚类的定义
聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。
1.2聚类的一般过程
数据准备：特征标准化和降维
特征选择：从最初的特征中选择最有效的特征，并将其存储在向量中
特征提取：通过对选择的特征进行转换形成新的突出特征
聚类：基于某种距离函数进行相似度度量，获取簇
聚类结果评估：分析聚类结果，如距离误差和(SSE)等
2.1 划分式聚类方法
划分式聚类方法需要事先指定簇类的数目或者聚类中心，通过反复迭代，直至最后达到"簇内的点足够近，簇间的点足够远"的目标。经典的划分式聚类方法有k-means及其变体k-means++、bi-kmeans、kernel k-means等。

2.1.2 k-means算法
经典的k-means算法的流程如下：