机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测
作者:AOAIYI
作者简介:Python领域新星作者、多项比赛获奖者:AOAIYI首页
😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒+关注哦!👍👍👍
📜📜📜如果有小伙伴需要数据集和学习交流,文章下方有交流学习区!一起学习进步!💪
| 专栏案例:机器学习 |
|---|
| 机器学习:基于逻辑回归对某银行客户违约预测分析 |
| 机器学习:学习k-近邻(KNN)模型建立、使用和评价 |
| 机器学习:基于支持向量机(SVM)进行人脸识别预测 |
| 决策树算法分析天气、周末和促销活动对销量的影响 |
| 机器学习:线性回归分析女性身高与体重之间的关系 |
| 机器学习:基于主成分分析(PCA)对数据降维 |
文章目录
- 机器学习:基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测
- 一、实验目的
- 二、实验原理
- 1.分类问题描述
- 2.Bayes’ theorem(贝叶斯法则)
- 3.朴素贝叶斯分类算法
- 三、实验环境
- 四、实验内容
- 五、实验步骤
- 1.朴素贝叶斯
- 2.业务理解
- 3.读取数据
- 4.数据理解
- 5.数据准备
- 6.构建数据训练集和测试集
- 7.构建三类模型
- 总结
一、实验目的
1.理解朴素贝叶斯的原理
2.掌握scikit-learn贝叶斯的用法
3.认识可视化工具seaborn
二、实验原理
1.分类问题描述
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法,对于分类问题,其实谁都不会陌生,日常生活中我们每天都进行着分类过程。例如,当你看到一个人,你的脑子下意识判断他是学生还是社会上的人;你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话,其实这就是一种分类操作,贝叶斯分类算法,那么分类的数学描述又是什么呢?

其中C叫做类别集合,其中每一个元素是一个类别,而I叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的内容是要求给定特征,构造分类器f,让我们得出类别。
2.Bayes’ theorem(贝叶斯法则)
在概率论和统计学中,Bayes theorem(贝叶斯法则)根据事件的先验知识描述事件的概率。贝叶斯法则表达式如下所示:
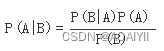
-
P(A|B) – 在事件B下事件A发生的条件概率
-
P(B|A) – 在事件A下事件B发生的条件概率
-
P(A), P(B) – 独立事件A和独立事件B的边缘概率
朴素贝叶斯方法是一组监督学习算法,它基于贝叶斯定理应用每对特征之间的“天真”独立假设。给定类变量y和从属特征矢量X1通过Xn,贝叶斯定理状态下列关系式:
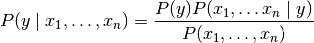
使用天真的独立假设
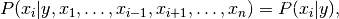
对所有人来说i,这种关系简化为
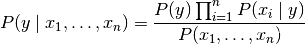
由于

输入是常数,我们可以使用以下分类规则:

我们可以使用最大后验(MAP)估计来估计的
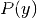 和
和 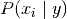
前者是y 训练集中类的相对频率。不同的朴素贝叶斯分类器主要区别于他们对分布的假设
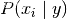
3.朴素贝叶斯分类算法
在scikit-learn中,提供了3种朴素贝叶斯分类算法:GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)
可以参考文档:
http://scikit-learn.org/stable/modules/naive_bayes.html
http://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html
三、实验环境
利用scikit-learn提供的三种朴素贝叶斯算法,构建分类器,根据花瓣花萼的宽度和长度判断他们属于哪一类
四、实验内容
Python 3.9
Jupyter notebook
五、实验步骤
1.朴素贝叶斯
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法
2.业务理解
先有一张表格,描述了花瓣的特征和种类,利用scikit-learn提供的三种朴素贝叶斯算法,构建分类器,根据花瓣花萼的宽度和长度预测他们属于哪一个品种
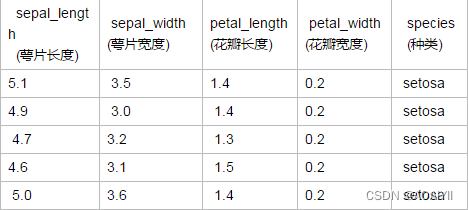
3.读取数据

1.编写代码,读取数据
#导入pandas库和numpy库
import pandas as pd
import numpy as np
iris = pd.read_csv(r'D:\CSDN\数据分析\naivebayes\iris.csv')
iris.head()
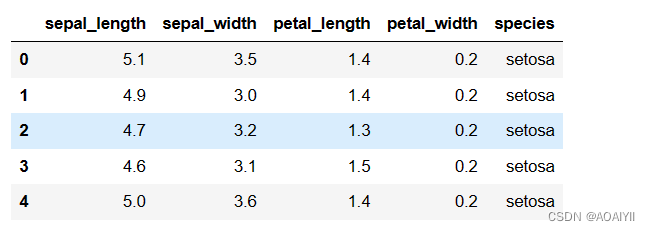
4.数据理解
1.查看数据结构
iris.shape

说明:该数据总共有150行,5列
2.查看数据列名称
iris.columns
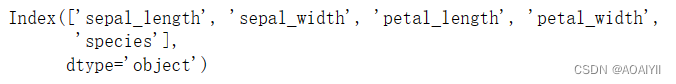
5.数据准备
1.删除“种类”这列数据得到特征数据如下:
X_iris = iris.drop(['species'],axis=1)
X_iris.head()
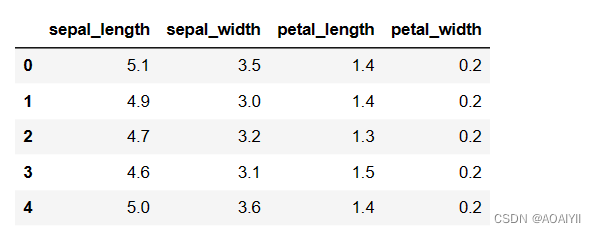
2.获取“species”这列数据并将其转换为数组,得到预测数据
y_iris = np.ravel(iris[['species']])
y_iris
3.查看y_iris总共有多少行
y_iris.shape

6.构建数据训练集和测试集
1.构建训练和测试数据集
#导入相应的库
from sklearn.model_selection import train_test_split
#将数据分为训练集,测试集
X_train,X_test,y_train,y_test = train_test_split(X_iris,y_iris,random_state=1)
#获取数据前5行
X_train.head()
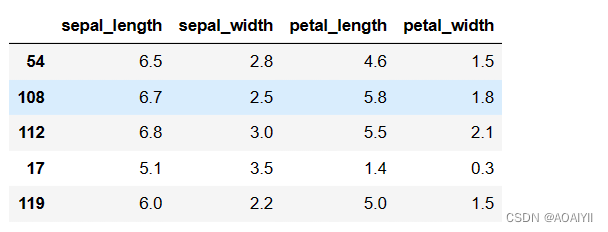
说明:将数据分为训练集和测试集,默认情况下,75%的数据用于训练,25%的数据用于测试
- 训练集是用于发现和预测潜在关系的一组数据。
- 测试集是用于评估预测关系强度和效率的一组数据。
2.查看训练集和测试集的数据结构
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

说明:训练集:X_iris数据为(150,4),X_train为(112,4),X_test为(38,4)
sales数据为200行,y_train为(112,),y_test为(38,)
3.查看y_train数据
y_train

7.构建三类模型
在scikit-learn中,提供了3种朴素贝叶斯分类算法:GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)
GaussianNB实现高斯朴素贝叶斯算法进行分类。假设特征的可能性是高斯的:
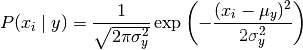
1.利用GaussianNB(高斯朴素贝叶斯)类建立简单模型并预测
from sklearn.naive_bayes import GaussianNB
#利用GaussianNB类建立简单模型
gb= GaussianNB()
model_GaussinaNB = gb.fit(X_train,y_train)
#predict(X):直接输出测试集预测的类标记,X_test为测试集
y_predict_GaussianNB= model_GaussinaNB.predict(X_test)
print("y_predict_GaussianNB",y_predict_GaussianNB)

构建一个新的测试数组
import pandas as pd
z_data ={'sepal_length':['5'],'sepal_width':['3'],'petal_length':['3'],'petal_width':['1.8']}
Z_data =pd.DataFrame(z_data,columns=['sepal_length','sepal_width','petal_length','petal_width'])
print(Z_data)

将测试数据带入模型预测得到预测结果
Z_model_predict=model_GaussinaNB.predict(Z_data)
print('Z_model_predict',Z_model_predict)
说明:当我们提供的数据为’sepal_length’:[‘5’],‘sepal_width’:[‘3’],‘petal_length’:[‘3’],‘petal_width’:[‘1.8’]时,预测它属于‘versicolor’这个种类,到底预测正确与否呢?接下来看一下预测结果的平均值
查看预测结果的平均值
#预测结果
y_predict_GaussianNB==y_test

mean()函数功能:求取均值
y_test_mean=np.mean(y_predict_GaussianNB==y_test)
print('y_test_GaussianNB_mean',y_test_mean)
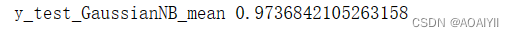
查看预测正确率
score(X, y[, sample_weight]) 返回给定测试数据和标签的平均精度
gb.score(X_train,y_train)
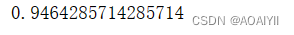
2.BernoulliNB(伯努利朴素贝叶斯)
BernoulliNB实现了根据多元伯努利分布的数据的朴素贝叶斯训练和分类算法; 即,可能存在多个特征,但每个特征被假定为二进制值(伯努利,布尔)变量。因此,该类要求将样本表示为二进制值特征向量;如果传递任何其他类型的数据,BernoulliNB实例可以将其输入二值化(取决于binarize参数)。
伯努利朴素贝叶斯的决策规则是基于
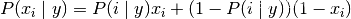
利用BernoulliNB类建立简单模型并预测
# ====================BernoulliNB
from sklearn.naive_bayes import BernoulliNB
model_BernoulliNB=BernoulliNB().fit(X_train,y_train)
y_predict_BernoulliNB=model_BernoulliNB.predict(X_test)
print('y_test_BernoulliNB_mean',np.mean(y_predict_BernoulliNB==y_test))
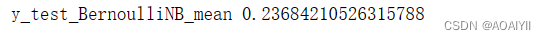
3.MultinomialNB(多项式朴素贝叶斯)
MultinomialNB实现用于多项分布数据的朴素贝叶斯算法,并且是用于文本分类的两种经典朴素贝叶斯变体之一(其中数据通常表示为单词向量计数,尽管tf-idf向量也已知在实践中很好地工作) 。
利用MultinomialNB类建立简单模型并预测
# ====================MultinomialNB
from sklearn.naive_bayes import MultinomialNB
model_MultinomialNB=MultinomialNB().fit(X_train,y_train)
y_predict_MultinomialNB=model_MultinomialNB.predict(X_test)
print('y_test_MultinomialNBB_mean',np.mean(y_predict_MultinomialNB==y_test))
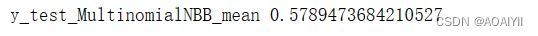
总结
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法,对于分类问题,其实谁都不会陌生,日常生活中我们每天都进行着分类过程。例如,当你看到一个人,你的脑子下意识判断他是学生还是社会上的人;你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话,其实这就是一种分类操作。
每个人都会遇到困难跟挫折,要有同困难作斗争的决心跟勇气。困难跟挫折是成就事业的基石,岸在远方向我们招手,只要越过它,敢于在惊涛骇浪中博击,我们就会尝到胜利的果食。