这篇文章是时间复杂度分析的第二篇。在前一篇文章中,我们从0推导出了为什么要用时间复杂度,时间复杂度如何分析以及时间复杂度的表示三部分内容。这篇文章,是对一些常用的时间复杂度进行一个总结,相当于是一个小结论
1.常见的大O阶
1.1线性阶
一般含有非嵌套循环(就是单层循环)涉及线性阶,线性阶就是随着输入规模的扩大,对应计算次数呈直线增长,例如下面的代码:
public static void main(String[] args) {
int sum = 0;
int n = 100;
for (int i = 1; i <=n ; i++) {
sum += i;
}
System.out.println("sum="+sum);
}上面这段代码,它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次
1.2平方阶
一般嵌套循环(就是双层循环)属于这种时间复杂度
public static void main(String[] args) {
int sum = 0;
int n = 100;
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
sum += i;
}
}
System.out.println("sum="+sum);
}上面这段代码,n=100,也就是说,外层循环每执行一次,内层循环就执行100次,那总共程序想要从这两个循环中出来,就需要执行100*100次,也就是n的平方次,所以这段代码的时间复杂度是O(n^2)
1.3立方阶
一般三层嵌套循环属于这种时间复杂度
public static void main(String[] args) {
int x = 0;
int n = 100;
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
for (int k = 1; k <=n ; k++) {
x ++;
}
}
}
System.out.println("x="+x);
}上面这段代码,n=100,也就是说,外层循环每执行一次,中间循环循环就执行100次,中间循环每执行一次,最内层循环需要执行100次,那总共程序想要从这三个循环中出来,就需要执行100*100*100次,也就是n的立方,所以这段代码的时间复杂度是O(n^3)
1.4对数阶
对数,属于高中数学的内容,我们分析程序以程序为主,数学为辅,所以不用过分担心。
public static void main(String[] args) {
int i = 0;
int n = 100;
while (i<n){
i = i*2;
}
System.out.println("i="+i);
}分析:
由于每次i*2之后,就距离n更近一步。我们假设有x个2相乘后大于n,那么x个2相乘后就会退出循环。那么就有公式:2^x=n,得到x=log(2)n。所以这个循环的时间复杂度为O(logn);
问:为什么底数可以忽略?
答:对于对数阶,由于随着输入规模n的增大,不管底数为多少,他们的增长趋势是一样的,所以我们会忽略底数。(其实就是找输入规模n与执行次数之间的抽象关系,抓取主要的,忽略次要的)
下面给出表和图,可以体会一下增长趋势:
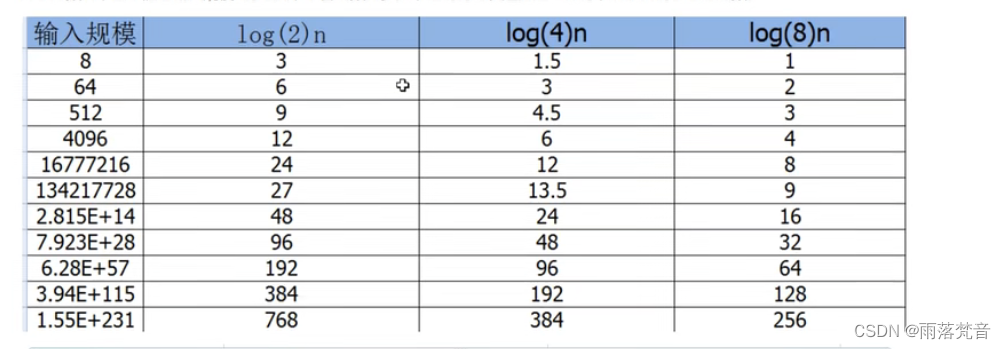
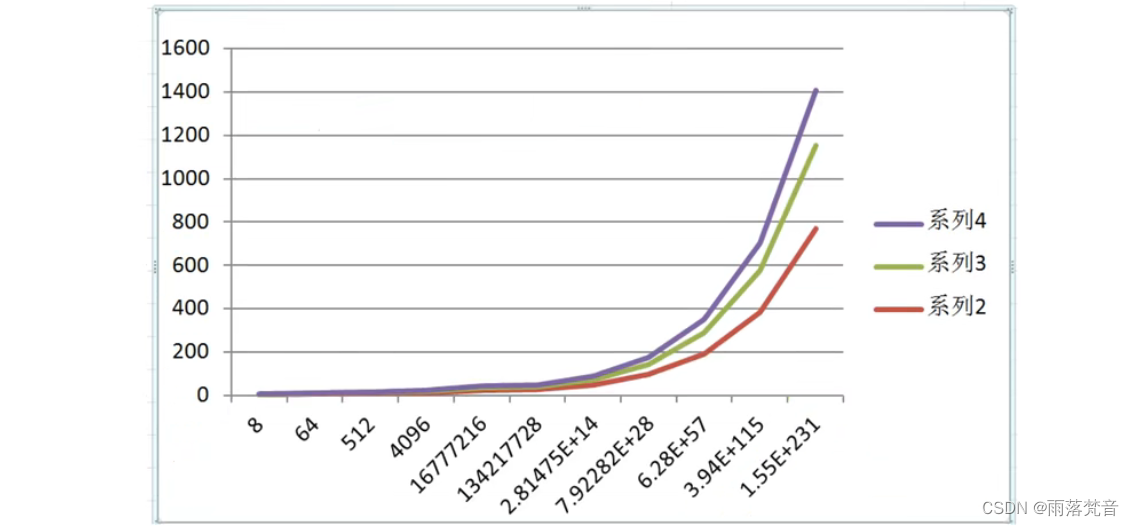
1.5常数阶
一般不涉及循环操作的都是常数阶,因为它不会随着n的增长而增加操作次数。例如︰
public static void main(String[] args) {
int n = 100;
int i = n+2;
System.out.println("i="+i);
}上述代码,不管输入规模n是多少,都执行2次,根据大O推导法则,常数用1来替换,所以上述代码的时间复杂度为O(1)
1.6小结
下面是对常见时间复杂度的一个总结:
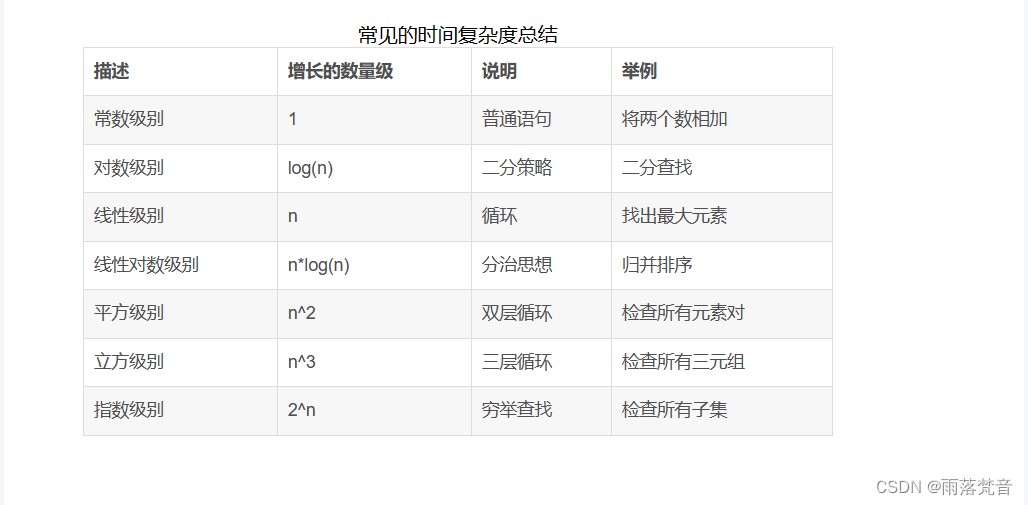
他们的时间复杂度从高到低依次是:
O(1)<O( log(n) )<O(n)<O(n*log(n))<O(n^2)<O(n^3)
根据前面的折线图分析,我们会发现,从平方阶开始,随着输入规模的增大,时间成本会急剧增大,所以,我们的算法,尽可能的追求的是O(1),O(log(n)),O(n),O(n^log(n))这几种时间复杂度,而如果发现算法的时间复杂度为平方阶、立方阶或者更复杂的,那我们可以分为这种算法是不可取的,需要优化。
2.函数调用的时间复杂度分析
之前,我们分析的都是单个函数内,算法代码的时间复杂度,接下来我们分析函数调用过程中时间复杂度。
2.1几个案例
案例一:
public static void main(String[] args) {
int n = 100;
for (int i = 0; i < n; i++) {
show(i);
}
}
public static void show(int i){
System.out.println(i);
}在main方法中,有一个for循环,循环体调用了show方法,由于show方法内部只执行了一行代码,所以show的时间复杂度为O(1),那main方法的时间复杂度就是O(n)
案例二:
public static void main(String[] args) {
int n = 100;
for (int i = 0; i < n; i++) {
show(i);
}
}
public static void show(int i){
for (int j = 0; j < i; j++) {
System.out.println(i);
}
}在main方法中,有一个for循环,循环体调用了show方法,由于show方法内部也有一个for循环,所以show方法的时间复杂度为O(n),那main方法的时间复杂度为O(n^2)
案例三:
public static void main(String[] args) {
int n = 100;
for (int i = 0; i < n; i++) {
show(i);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println(j);
}
}
}
public static void show(int i){
for (int j = 0; j < i; j++) {
System.out.println(i);
}
}在show方法中,有一个for循环,所以show方法的时间复杂度为o(n),在main方法中,show(n)这行代码内部执行的次数为n,第一个for循环内调用了show方法,所以其执行次数为n^2,第二个嵌套for循环内只执行了一行代码,所以其执行次数为n^2,那么main方法总执行次数为n+n^2+n^2=2n^2+n。
根据大O推导规则,去掉n保留最高阶项,并去掉最高阶项的常数因子2,所以最终main方法的时间复杂度为O(n^2)
2.2最坏情况
从心理学角度讲,每个人对发生的事情都会有一个预期,比如看到半杯水,有人会说︰哇哦,还有半杯水哦!但也有人会说∶天哪,只有半杯水了。一般人处于一种对未来失败的担忧,而在预期的时候趋向做最坏的打算,这样即使最糟糕的结果出现,当事人也有了心理准备,比较容易接受结果。假如最糟糕的结果并没有出现,当事人会很快乐。
算法分析也是类似,假如有一个需求∶
有一个存储了n个随机数字的数组,请从中查找出指定的数字。
public static void main(String[] args) {
int a = search(5);
System.out.println(a);
}
public static int search(int num){
int[] arr = {11,5,3,6,7,15,6,9};
for (int i = 0; i < arr.length; i++) {
if (num == arr[i]) {
return i;
}
}
return -1;
}最好情况:
查找的第一个数字就是期望的数字,那么算法的时间复杂度为O(1)
最坏情况:
查找的最后一个数字,才是期望的数字,那么算法的时间复杂度为O(n)
平均情况:
任何数字查找的平均成本是O(n/2)
最坏情况是一种保证,在应用中,这是一种最基本的保障,即使在最坏情况下,也能够正常提供服务,所以,除非特别指定,我们提到的运行时间都指的是最坏情况下的运行时间。
3.小结
这篇文章,我们总结了一些常见的大O阶,然后给出了相应的表格,这属于是一种结论,可以记下来的。然后我们分析了函数调用时的时间复杂度,其实和之前的分析方法是一样的。最后,我们讲了一下最坏情况的分析。
至此,算法的时间复杂度的讲解已经完毕了。如果有失误的地方,敬请各位指出,谢谢大家!