题目链接：84. 柱状图中最大的矩形

题目描述：

                给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

                求在该柱状图中，能够勾勒出来的矩形的最大面积。

解法：

                ①此题求最大能勾勒出的矩形面积，那么我们就求每个柱子能勾勒出的矩形的面积，然后取最大值。

                ②每个柱子能勾勒出的矩形面积 = （右边第一个比其矮的柱子的坐标 - 左边第一个比它矮的柱子的坐标 -  1）* 该柱子的高度。

                ③在找左边或者右边第一比它矮的柱子的坐标的时候，如果左边的比当前的高，那么就变换t为此时的第一个比左边的柱子小的柱子的位置，直到左边比当前的矮就结束。

                ④同理找右边第一个比它矮的柱子的坐标。

                ⑤最后取最大值即可。

下面为代码（java）：

 

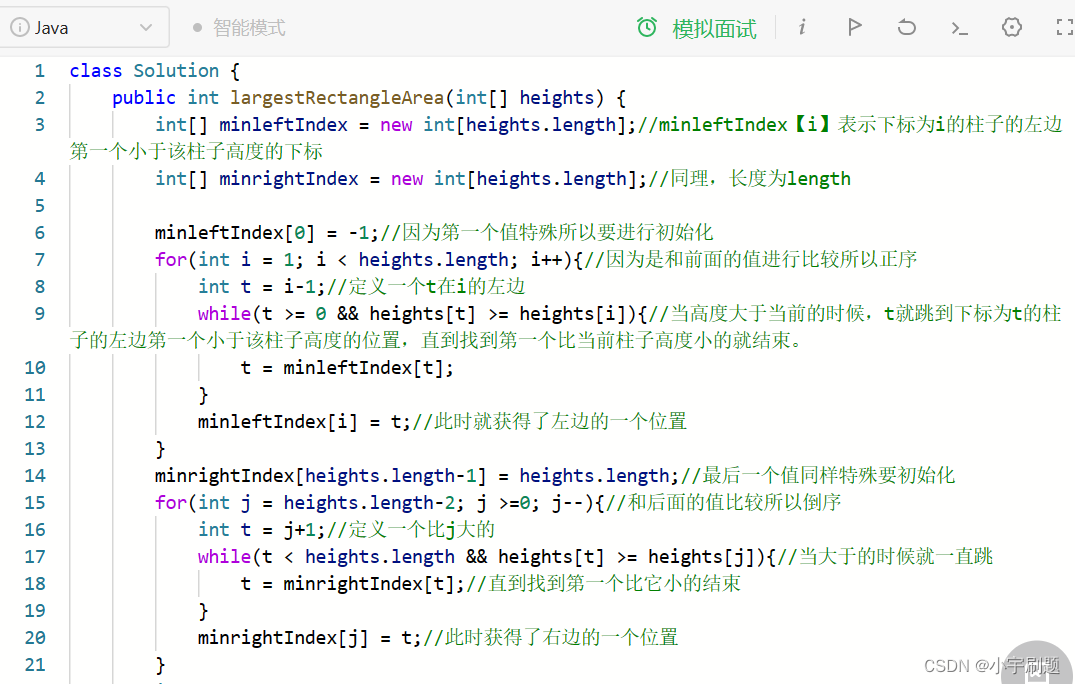
总结：

                每个柱子能形成的矩形面积 = （右边第一个比当前柱子高度矮的位置 - 左边第一个比当前柱子高度矮的位置） * 当前柱子高度。