TopK问题介绍：

在N个数中找出最大/小的前K个 （比如在1000个数中找出最大/小的前10个）

以前的方法：冒泡排序。时间复杂度： O(N^2)

现在找最大的k个数的方法：

方法1：堆排序降序，前N个就是最大的。上篇学过时间复杂度： O(N*logN)

方法2：N个数依次插入大堆，HeapPop K次，每次取堆顶的数据，即为前K个。

时间复杂度： O(K*logN)

假设 N非常大， 是 10 亿，内存中存不下这些数，它们存在文件中的。 K是 100，
上面的方法就都不能用了……
话说 10 亿个整数，大概占用多少空间？
1G = 1024MB
1G = 1024*1024KB
1G = 1024*1024*1024Byte
要占用10亿字节！所以我们来看看方法3：

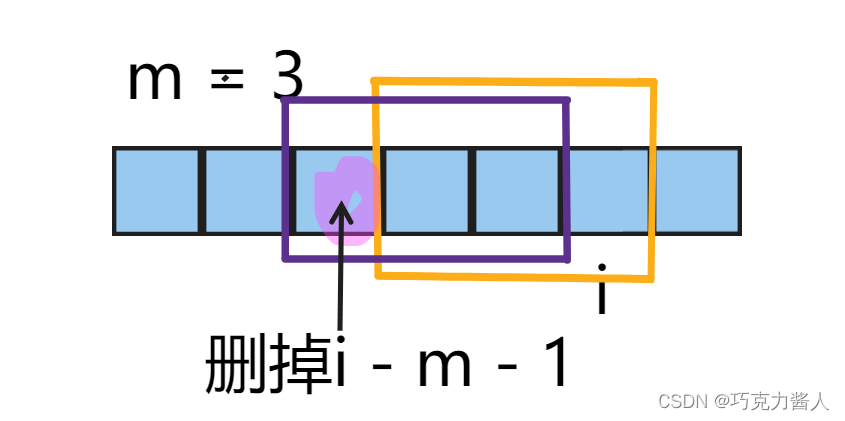
方法3：

这里为什么使用小堆而不使用大堆？

最大的前K个数一定会比其他数要大，只要进来的数比堆顶数据大，就替代它。

因为是小堆（小的在上大的在下），最大的数进去后一定会沉到下面，

所以不可能存在大的数堵在堆顶导致某个数进不去的情况，数越大沉得越深。

对应地，如果使用大堆就会出现一个大数堵在堆顶，剩下的数都比这个大数小，

导致其他数进不来，最后只能选出最大的那一个。

剑指 Offer 40. 最小的k个数

难度简单

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，

则最小的4个数字是1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2

输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1

输出：[0]

限制：

• 0 <= k <= arr.length <= 10000

• 0 <= arr[i] <= 10000

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){

}

解析代码：

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void justDown(int* arr, int n, int root)//大堆下调
{
    int father = root;
    int child = father * 2 + 1;//默认左孩子大
    while (child < n)
    {
        if (child + 1 < n && arr[child] < arr[child + 1])
        {  // 如果右孩子存在且右孩子比左孩子大
            child++;
        }
        if (arr[father] < arr[child])
        {
            int tmp = arr[father];
            arr[father] = arr[child];
            arr[child] = tmp;

            father = child;
            child = father * 2 + 1;
        }
        else
        {
            break;
        }
    }
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize) {
    *returnSize = k;
    if (k == 0)//回头处理k==0
    {
        return NULL;
    }
    int* retArr = (int*)malloc(sizeof(int) * k);
    for (int i = 0;i < k;i++)
    {
        retArr[i] = arr[i];
    }
    for (int i = (k - 1 - 1) / 2;i >= 0;i--) //建堆的for写法
    {
        justDown(retArr, k, i);
    }
    for (int j = k;j < arrSize;j++)
    {
        if (arr[j] < retArr[0])
        {
            retArr[0] = arr[j];
            justDown(retArr, k, 0);
        }
    }
    //*returnSize = k; 写到这发现有个测试用例跑不了，到上面处理一下
    return retArr;
}