先看题目：

说实话，我看到这道题就想用滑动窗口，但是滑了一下发现不太对啊，如果我用滑动窗口的话，那么最后肯定是一个固定长度为m的窗口在持续计算，区间长度小于m的区间的异或和肯定会被遗漏。然后我就想怎么用Trie树来解决这道题，但是我没想明白呜呜呜。

所以前去看了y总的视频题解。

先大致说一下什么是Trie树好了，Trie也叫字典树，它的核心就是通过存储不同字符串的公共前缀来减少查找字符串的时间。

 

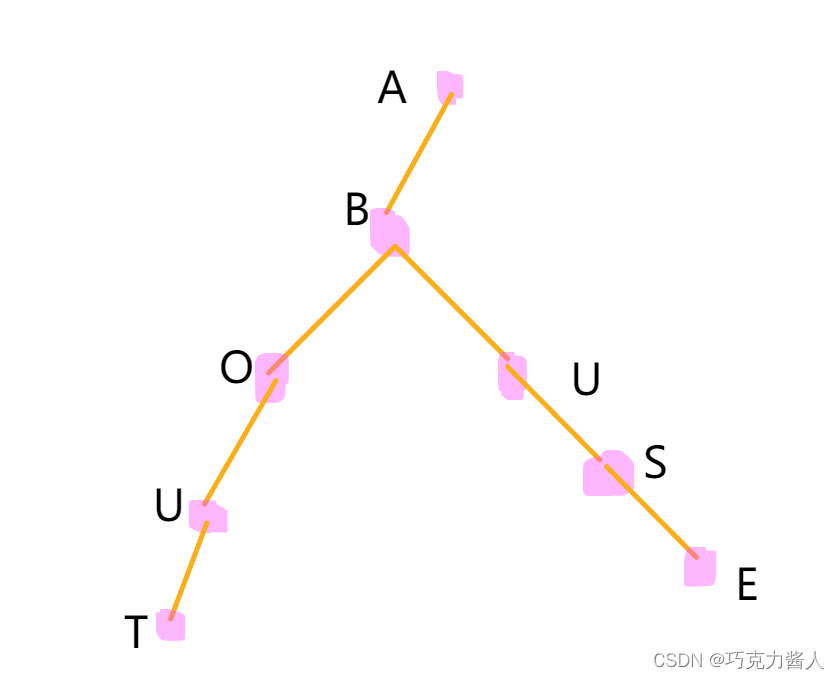
看图，对于abuse和about这两个字符串，我们想把他们放到Trie树种，发现他们俩有共同的前缀ab，所以就在b后面开始分叉，然后各走各的分叉。

这道题就是在这个基础上做的。

然后这道题求的是区间的异或和，所以我们还得知道异或的一个特性。我们遍历数组，计算每个前缀的异或和，如果我们想要计算一个区间[i,j]的异或值，那么我们就可以用s[i,j]=s[j]^s[i - 1]求取。为什么可以这么算呢？这是因为一个数和本身异或，结果为0.

好，又一个知识点出来了。

那么现在开始看题：

因为数据范围是2^31-1，那么异或和也最多是31位二进制，也就是说最多是31位二进制就能表示每个数字，那么从0到30就对应异或和的二进制位。

先不考虑区间长度最大为M，我们要找到的是最大的异或和，怎么怎么找呢？

目前我们在Trie树中存储了j以前的前缀异或和，如果想找到一个前缀异或和s[i]和s[j]的异或结果最大的话，应该怎么处理呢？

我们知道异或的计算方法：1^0 = 1, 0 ^ 0 = 0, 1 ^ 1 = 0;那么现在我们有一个s[j]，想得到一个和它异或后的最大结果，就要保证最高位尽可能地不同。

假如s[j] = 10101001,那么我们在遍历这棵Trie树的时候，希望能够找到最高位为0的节点，这样才能使异或结果的最高位为1，如果找不到为0的节点，那么只好找最高位为1的节点，尽量保证接下来遍历的节点和s[j]的异或结果为1好了。

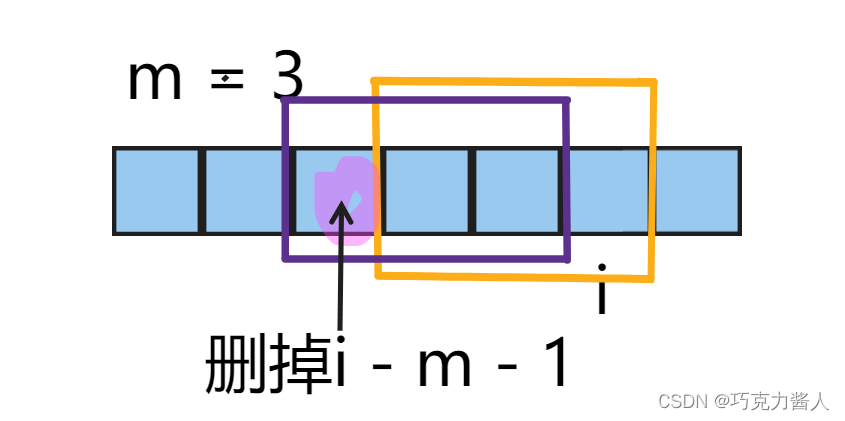
这个就是当区间长度不限时我们的计算方式，但是现在题目要求长度最大为M，怎么办呢？去Trie树中删掉吗，好像有点难呢。我们在这里采用伪装删除的方法，用cnt记录经过这个节点的元素的个数。如果要删除某个元素，那么就找到这个元素对应的最后一个结束节点，把它的cnt值-1好了。所以如果我们发现当前遍历到了i>m的前缀异或，为了保证窗口中最多有m个异或和，我们必须删除最前面的异或和，也就是s[i - m - 1]这个异或和了。

 

代码来喽：

#include<iostream>
#include<cstdio>
#include<vector>
#include<map>
#include<cmath>
#include<cstring>
#include<algorithm>
//#define ll long long
const int N = 100010 * 31;  //最多是1e5，每个数最多31位，所以最多一共31*1e5个节点
int cnt[N];
int s[N];  //前缀异或和 
int son[N][2];
int idx;
using namespace std;
void insert(int x, int v){
	int p = 0;
	for(int i = 30; i >= 0; i--){  
		int u = (x >> i) & 1;
		//如果当前节点没有这个分叉，那么我们就新建一个分叉，这个idx可以认为是不同分叉的编号
		//用这个idx可以获取到每个分叉，然后就可以从这个分叉接着往下走了
		if(!son[p][u]) son[p][u] = ++idx;  
		p = son[p][u];  //从这个分叉往下走
		cnt[p] += v;  //经过这个分叉的元素的个数+1或者-1，增加一个元素或者删除一个元素
	} 
} 
int query(int x){
	int res = 0;
	int p = 0;
	for(int i = 30; i >= 0; i--){ //一定要从最高位开始往下，因为我们希望能够保证最高位最大 
		int u = x >> i & 1;
		if(cnt[son[p][!u]]) {  //能够保证和当前位不同，异或结果为1
			p = son[p][!u];
			//在整理这个异或和，当前位异或值为1，可以认为之前的结果为res，
			//现在在res后面又加了一位1，那么现在的结果就是res*2+1
			res = res * 2 + 1;  
		}
		else {
			p = son[p][u];
			res = res * 2;
		}
	}
	return res; 
}
int main(){
	int n, m;
	scanf("%d%d", &n, &m);
	int x;
	for(int i = 1; i <= n; i++){
		scanf("%d", &x);
		s[i] = s[i - 1] ^ x; 
	}
	int res = 0;
	insert(s[0], 1);  //1代表插入一个数
	for(int i = 1; i <= n; i++){
	     //删除最前面的元素，例如当i = m+1，那么就把s[0]删除，因为他不在长度为m的窗口内部了。
	     //现在树中有
		if(i > m) insert(s[i - m - 1], -1); 
		res = max(res, query(s[i]));  //找到和s[i]异或后的最大结果
		insert(s[i], 1); //别忘了把这个添加到树中
	} 
	printf("%d\n", res);
	return 0;
}