1 主要思想

分类就是分割数据：

• 两个条件属性：直线；
• 三个条件属性：平面；
• 更多条件属性：超平面。

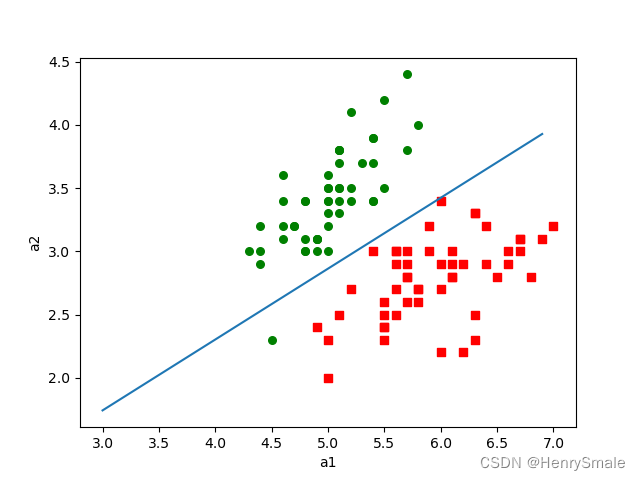
使用数据：

5.1,3.5,0
4.9,3,0
4.7,3.2,0
4.6,3.1,0
5,3.6,0
5.4,3.9,0
. . .
6.2,2.9,1
5.1,2.5,1
5.7,2.8,1
6.3,3.3,1

2 理论

2.1 线性分割面的表达

平面几何表达直线(两个系数)：
$$y=ax+b.$$

重新命名变量：
$$w_0+w_1{x}_1+w_2{x}_2=0.$$

强行加一个$x_0\equiv 1$：
$$w_0{x}_0+w_1{x}_1+w_2{x}_2=0.$$

向量表达($\mathbf{x}$为行向量, $\mathbf{w}$为列向量,)
$$\mathbf{xw}=0.$$

2.2 学习与分类

• Logistic regression的学习任务，就是计算向量$\mathbf{w}$;
• 分类（两个类别）：对于新对象${\mathbf{x}}^{\prime }$，计算${\mathbf{x}}^{\prime }\mathbf{w}$，结果小于0则为0类，否则为1类；
• 线性模型（加权和）是机器学习诸多主流方法的核心。

2.3 基本思路

2.3.1 第一种损失函数：

$\mathbf{w}$在训练集中$(\mathbf{X},\mathbf{Y})$表现要好。
Heaviside跃迁函数为
$$H(z)=\{\begin{array}{ll}0,& \text{ if }z<0,\\ \frac{1}{2},& \text{ if }z=0,\\ 1,& \text{ otherwise.}\end{array}$$
令 X = { x 1 , … , x m } \mathbf{X} = \{\mathbf{x}_1, \dots, \mathbf{x}_m\} X={x1​,…,xm​}, 错误率即：
$$\frac{1}{m}\sum _{i=1}^m|H({\mathbf{x}}_i\mathbf{w})-y_i|,$$
其中$H({\mathbf{x}}_i\mathbf{w})$是分类器给的标签，而$y_i$是实际标签。

• 优点：表达了错误率；
• 缺点：函数$H$不连续，无法使用优化理论。

2.3.2 第二种损失函数

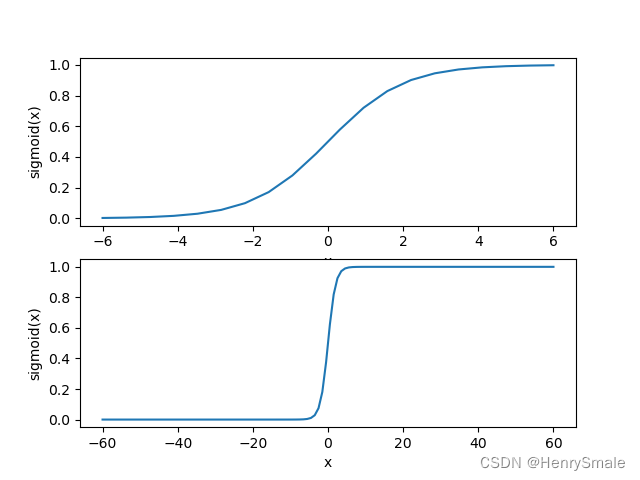
Sigmoid函数：
$$\sigma (z)=\frac{1}{1+e^{-z}}.$$
优点：连续，可导。

Sigmoid函数的导数：
$$\begin{array}{ll}{\sigma }^{\prime }(z)& =\frac{d}{dz}\frac{1}{1+e^{-z}}\\ & =-\frac{1}{(1+e^{-z}{)}^2}(e^{-z})(-1)\\ & =\frac{e^{-z}}{(1+e^{-z}{)}^2}\\ & =\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})\\ & =\sigma (z)(1-\sigma (z)).\end{array}$$

令${\hat{y}}_i=\sigma ({\mathbf{x}}_i\mathbf{w})$,
$$\frac{1}{m}\sum _{i=1}^m\frac{1}{2}({\hat{y}}_i-y_i{)}^2,$$
其中平方使得函数连续可导，$\frac{1}{2}$是为了适应求导的惯用手法。

缺点：非凸优化, 多个局部最优解

2.3.3 凸与非凸

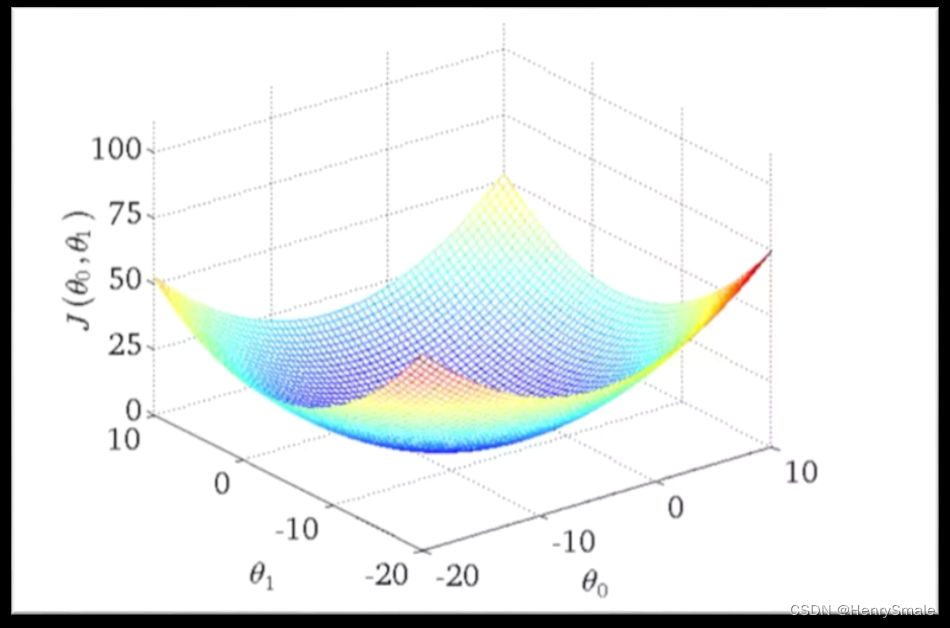
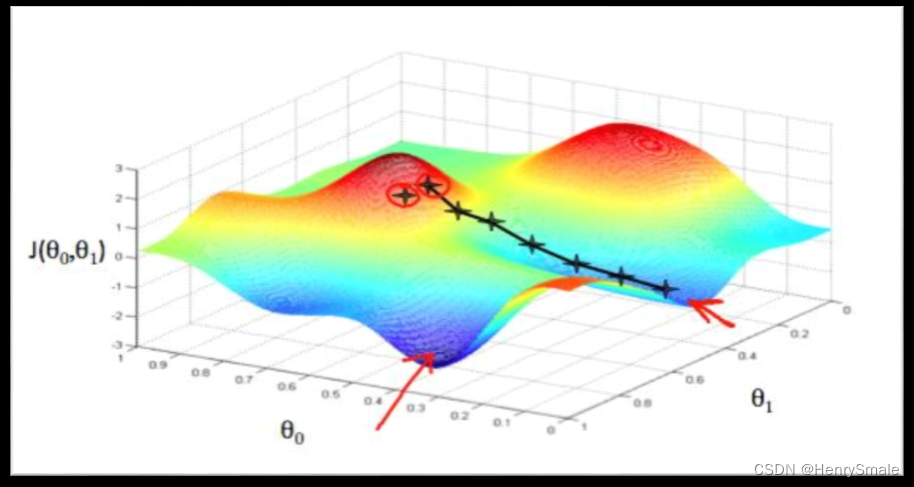
2.3.4 第三种损失函数(强行看作概率)

由于$0<\sigma (z)<1$, 将$\sigma ({\mathbf{x}}_i\mathbf{w})$看作类别为1的概率, 即
$$P(y_i=1|{\mathbf{x}}_i;\mathbf{w})=\sigma ({\mathbf{x}}_i\mathbf{w}),$$
其中${\mathbf{x}}_i$是条件, $\mathbf{w}$是参数。

相应地
$$P(y_i=0|{\mathbf{x}}_i;\mathbf{w})=1-\sigma ({\mathbf{x}}_i\mathbf{w}),$$
综合上两式, 可得
$$P(y_i|{\mathbf{x}}_i;\mathbf{w})=(\sigma ({\mathbf{x}}_i\mathbf{w}){)}^{y_i}(1-\sigma ({\mathbf{x}}_i\mathbf{w}){)}^{1-y_i}$$

该值越大越好。
假设训练样本独立, 且同等重要。
为获得全局最优, 将不同样本涉及的概率连乘, 获得似然函数：
$$\begin{array}{ll}L(\mathbf{w})& =P(\mathbf{Y}|\mathbf{X};\mathbf{w})\\ & ={\prod }_{i=1}^{m}P(y_i|{\mathbf{x}}_i;\mathbf{w})\\ & ={\prod }_{i=1}^m(\sigma ({\mathbf{x}}_i\mathbf{w}){)}^{y_i}(1-\sigma ({\mathbf{x}}_i\mathbf{w}){)}^{1-y_i}\end{array}$$
对数函数具有单调性：
$$\begin{array}{ll}l(\mathbf{w})& =\log L(\mathbf{w})\\ & =\log {\prod }_{i=1}^{m}P(y_i|{\mathbf{x}}_i;\mathbf{w})\\ & ={\sum }_{i=1}^m{y}_i\log \sigma ({\mathbf{x}}_i\mathbf{w})+(1-y_i)\log (1-\sigma ({\mathbf{x}}_i\mathbf{w}))\end{array}$$

平均损失：

• $L(\mathbf{w})$, $l(\mathbf{w})$越大越好；
• $l(\mathbf{w})$为负值；
• 求相反数, 除以实例个数, 损失函数：

$$\frac{1}{m}\sum _{i=1}^m-y_i\log \sigma ({\mathbf{x}}_i\mathbf{w})-(1-y_i)\log (1-\sigma ({\mathbf{x}}_i\mathbf{w})).$$

分析：

• $y_i=0$ 时退化为$-\log (1-\sigma ({\mathbf{x}}_i\mathbf{w}))$, $\sigma ({\mathbf{x}}_i\mathbf{w})$越接近0越损失越小;
• $y_i=1$ 时退化为$-\log \sigma ({\mathbf{x}}_i\mathbf{w})$, $\sigma ({\mathbf{x}}_i\mathbf{w})$越接近1越损失越小。

优化目标：
$$\underset{\mathbf{w}}{\min }\frac{1}{m}\sum _{i=1}^m-y_i\log \sigma ({\mathbf{x}}_i\mathbf{w})-(1-y_i)\log (1-\sigma ({\mathbf{x}}_i\mathbf{w})).$$

2.4 梯度下降法

梯度下降法是机器学习的一种主流优化方法

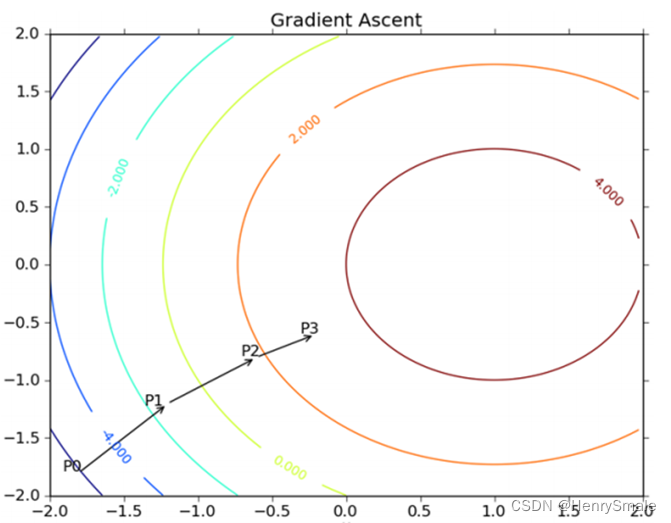
迭代式推导：
由于
$$l(\mathbf{w})=\sum _{i=1}^m{y}_i\log \sigma ({\mathbf{x}}_i\mathbf{w})+(1-y_i)\log (1-\sigma ({\mathbf{x}}_i\mathbf{w}))$$
$$\begin{array}{ll}\frac{\partial l(\mathbf{w})}{\partial w_j}& ={\sum }_{i=1}^m\left(\frac{y_i}{\sigma ({\mathbf{x}}_i\mathbf{w})}-\frac{1-y_i}{1-\sigma ({\mathbf{x}}_i\mathbf{w})}\right)\frac{\partial \sigma ({\mathbf{x}}_i\mathbf{w})}{\partial w_j}\\ & ={\sum }_{i=1}^m\left(\frac{y_i}{\sigma ({\mathbf{x}}_i\mathbf{w})}-\frac{1-y_i}{1-\sigma ({\mathbf{x}}_i\mathbf{w})}\right)\sigma ({\mathbf{x}}_i\mathbf{w})(1-\sigma ({\mathbf{x}}_i\mathbf{w}))\frac{\partial {\mathbf{x}}_i\mathbf{w}}{\partial w_j}\\ & ={\sum }_{i=1}^m\left(\frac{y_i}{\sigma ({\mathbf{x}}_i\mathbf{w})}-\frac{1-y_i}{1-\sigma ({\mathbf{x}}_i\mathbf{w})}\right)\sigma ({\mathbf{x}}_i\mathbf{w})(1-\sigma ({\mathbf{x}}_i\mathbf{w}))x_{ij}\\ & ={\sum }_{i=1}^m(y_i-\sigma ({\mathbf{x}}_i\mathbf{w}))x_{ij}\end{array}$$

3 程序分析

3.1 Sigmoid函数

return 1.0/(1 + np.exp(-paraX))

3.2 使用sklearn

#Test my implemenation of Logistic regression and existing one.
import time, sklearn
import sklearn.datasets, sklearn.neighbors, sklearn.linear_model
import matplotlib.pyplot as plt
import numpy as np

"""
The version using sklearn，支持多个决策属性值
"""
def sklearnLogisticTest():
    #Step 1. Load the dataset
    tempDataset = sklearn.datasets.load_iris()
    x = tempDataset.data
    y = tempDataset.target

    #Step 2. Classify
    tempClassifier = sklearn.linear_model.LogisticRegression()
    tempStartTime = time.time()
    tempClassifier.fit(x, y)
    tempScore = tempClassifier.score(x, y)
    tempEndTime = time.time()
    tempRuntime = tempEndTime - tempStartTime

    #Step 3. Output
    print('sklearn score: {}, runtime = {}'.format(tempScore, tempRuntime))

"""
The sigmoid function, map to range (0, 1)
"""
def sigmoid(paraX):
    return 1.0/(1 + np.exp(-paraX))

"""
Illustrate the sigmoid function.
Not used in the learning process.
"""
def sigmoidPlotTest():
    xValue = np.linspace(-6, 6, 20)
    #print("xValue = ", xValue)
    yValue = sigmoid(xValue)
    x2Value = np.linspace(-60, 60, 120)
    y2Value = sigmoid(x2Value)
    fig = plt.figure()
    ax1 = fig.add_subplot(2, 1, 1)
    ax1.plot(xValue, yValue)
    ax1.set_xlabel('x')
    ax1.set_ylabel('sigmoid(x)')
    ax2 = fig.add_subplot(2, 1, 2)
    ax2.plot(x2Value, y2Value)
    ax2.set_xlabel('x')
    ax2.set_ylabel('sigmoid(x)')
    plt.show()

"""
函数：梯度上升算法，核心
"""
def gradAscent(dataMat,labelMat):
    dataSet = np.mat(dataMat)                          # m*n
    labelSet = np.mat(labelMat).transpose()            # 1*m->m*1
    m, n = np.shape(dataSet)                            # m*n: m个样本，n个特征
    alpha = 0.001                                      # 学习步长
    maxCycles = 1000                                    # 最大迭代次数
    weights = np.ones( (n,1) )
    for i in range(maxCycles):
        y = sigmoid(dataSet * weights)                 # 预测值
        error = labelSet - y
        weights = weights + alpha * dataSet.transpose() * error
    return weights

"""
函数：画出决策边界，仅为演示用，且仅支持两个条件属性的数据
"""
def plotBestFit(paraWeights):
    dataMat, labelMat = loadDataSet()
    dataArr=np.array(dataMat)
    m,n=np.shape(dataArr)
    x1=[]           #x1,y1:类别为1的特征
    x2=[]           #x2,y2:类别为2的特征
    y1=[]
    y2=[]
    for i in range(m):
        if (labelMat[i])==1:
            x1.append(dataArr[i,1])
            y1.append(dataArr[i,2])
        else:
            x2.append(dataArr[i,1])
            y2.append(dataArr[i,2])

    fig=plt.figure()
    ax=fig.add_subplot(111)
    ax.scatter(x1,y1,s=30,c='red',marker='s')
    ax.scatter(x2,y2,s=30,c='green')

    #画出拟合直线
    x=np.arange(3, 7.0, 0.1)
    y=(-paraWeights[0]-paraWeights[1]*x)/paraWeights[2]    #直线满足关系：0=w0*1.0+w1*x1+w2*x2
    ax.plot(x,y)
 
    plt.xlabel('a1')
    plt.ylabel('a2')
    plt.show()

"""
读数据, csv格式
"""
def loadDataSet(paraFilename="data/iris2class.txt"):
    dataMat=[]  #列表list
    labelMat=[]
    txt=open(paraFilename)
    for line in txt.readlines():
        tempValuesStringArray = np.array(line.replace("\n", "").split(','))
        tempValues = [float(tempValue) for tempValue in tempValuesStringArray]
        tempArray = [1.0] + [tempValue for tempValue in tempValues]
        tempx = tempArray[:-1] #不要最后一列
        tempy = tempArray[-1] #仅最后一列
        
        dataMat.append(tempx)
        labelMat.append(tempy)
        
    #print("dataMat = ", dataMat)
    #print("labelMat = ", labelMat)
    return dataMat,labelMat

"""
Logistic regression分类
"""
def mfLogisticClassifierTest():
    #Step 1. Load the dataset and initialize
    #如果括号内不写数据，则使用4个属性前2个类别的iris
    x, y = loadDataSet("data/iris2condition2class.csv")
    
    #tempDataset = sklearn.datasets.load_iris()
    #x = tempDataset.data
    #y = tempDataset.target

    tempStartTime = time.time()
    tempScore = 0
    numInstances = len(y)
    #Step 2. Train
    weights = gradAscent(x, y)

    #Step 2. Classify
    tempPredicts = np.zeros((numInstances))

    #Leave one out
    for i in range(numInstances):
        tempPrediction = x[i] * weights
        #print("x[i] = {}, weights = {}, tempPrediction = {}".format(x[i], weights, tempPrediction))
        if tempPrediction > 0:
            tempPredicts[i] = 1
        else:
            tempPredicts[i] = 0

    #Step 3. Which are correct?
    tempCorrect = 0
    for i in range(numInstances):
        if tempPredicts[i] == y[i]:
            tempCorrect += 1

    tempScore = tempCorrect / numInstances
    
    tempEndTime = time.time()
    tempRuntime = tempEndTime - tempStartTime

    #Step 4. Output
    print('Mf logistic socre: {}, runtime = {}'.format(tempScore, tempRuntime))

    #Step 5. Illustrate 仅对两个属性情况有效
    rowWeights = np.transpose(weights).A[0]
    plotBestFit(rowWeights)
    
def main():
    #sklearnLogisticTest()
    mfLogisticClassifierTest()
    #sigmoidPlotTest()

main()