1. 简介
您是否曾经遇到过这样一种情况:您试图分析一个复杂且高度相关的数据集,却对信息量感到不知所措?这就是独立成分分析 (ICA) 的用武之地。ICA 是数据分析领域的一项强大技术,可让您分离和识别多元数据集中的底层独立来源。
ICA 之所以重要,是因为它提供了一种理解数据集隐藏结构的方法,可用于各种应用,例如信号处理、脑成像、金融和许多其他领域。此外,ICA 可以帮助从数据中提取最相关的信息,提供有价值的见解,否则这些见解将在大量相关性中丢失。
在本文[1]中,我们将深入探讨ICA 的基础知识,ICA 算法,以及如何在数据分析项目中实施它。
2. 主要思想
独立成分分析是各种无监督学习算法中的一种,这意味着我们在使用模型之前不需要对其进行监督。这种方法的起源来自信号处理,我们试图将多变量信号分离成加性子分量。让我们进入对主要思想的解释:
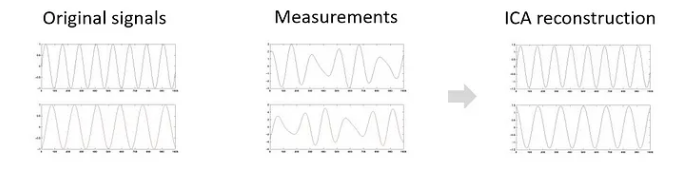
想象一些独立的信号或变量。这些信号可以表示为信号曲线,在上图中,第一个信号位于顶部,第二个信号位于底部。作为测量的结果,我们没有收到包含信号本身的数据集,而是包含这两个信号的测量值的数据集,不幸的是,这两个信号被混合成不同的线性组合。 ICA 的目标是通过分离混合数据来恢复原始的未知信号。最终目的是重建数据,使每个维度相互独立。
为了使这个概念更具体,将使用 ICA 最著名的例子,即“鸡尾酒会问题”。
2.1. 鸡尾酒会问题
想象一下,参加一个多人同时发言的鸡尾酒会,很难听懂一个人的谈话。值得注意的是,在这种情况下,人类具有分离个人语音流的能力。从技术上讲,这变得有点具有挑战性。

假设我们使用两个麦克风记录聚会中两组的对话。这会导致两个混合信号,其中第一次测量对第一组的影响较大,对第二组的影响较小,而第二次测量对第二组的影响较大。

这个的一般框架可以在灰色框中用矢量符号表示。矢量 X 中的测量实际上是矢量 S 的信号乘以一些混合系数,在矩阵 A 中表示。由于我们想要提取完整的对话(原始信号),我们需要为矢量 S 解决这个问题。

2.2. ICA vs. PCA
您可能已经猜到 ICA 在某种程度上与主成分分析 (PCA) 相关。这个假设并没有错。这两个概念背后的想法相差不大,但它们在最后阶段有所不同,我们将在后面看到。
让我们总结一下 PCA 的基本作用:假设我们有两个看起来相关的变量。通过使用这些变量的特征向量和特征值最大化方差,我们可以将它们转换为主成分。在此特定示例中,PCA 很好地识别了此关系的主要方向。
让我们以前面的鸡尾酒示例为例。在一个非常简单的表示中,我们可以想象来自麦克风 1 和 2 的两个测量值具有形成类似交叉模式的关系。如果我们在这种情况下应用 PCA,我们会得到错误的结果,因为 PCA 无法处理具有多个主要方向的数据集。
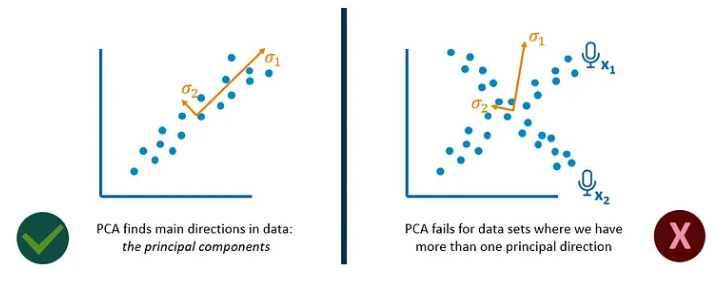
另一方面,ICA 通过关注独立成分而不是主要成分来解决这个问题。
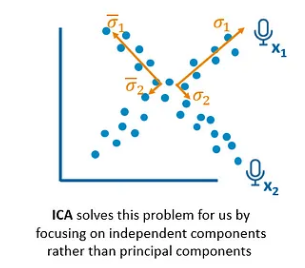
重要的是要回顾既定的概念框架。从麦克风获得的读数对应于已乘以混合矩阵 A 的原始信号。通过关于向量 S 重新排列方程,确定原始变量的唯一必要信息是矩阵 A。然而,矩阵 A 是未知的.

因此,要全面了解矩阵A并最终计算出向量S,需要通过一系列步骤进行逆运算。这些连续的逆运算构成了 ICA 算法的三个阶段,现在将对其进行更详细的分析。
3. ICA 算法
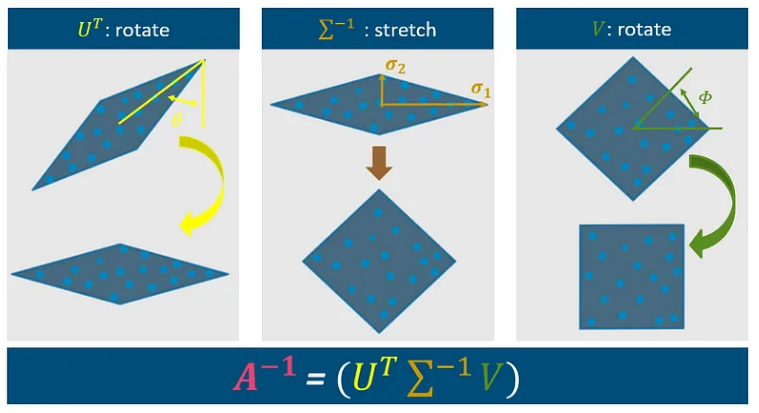
在进行 R 中的实际演示之前,了解算法的三个步骤很重要。该算法的目标是执行向量 X 与矩阵 A 的乘法。矩阵 A 由三个组成部分组成,它们是不同因素之间相乘相互作用的结果:
3.1. Step 1
-
找到具有最大方差的角度来旋转 |估计 U^T
该算法的第一个组成部分涉及使用基于第一个角度 Theta 的矩阵 U^T。角度 Theta 可以从数据的主要方向导出,如通过主成分分析 (PCA) 确定的那样。此步骤将图形旋转到如上所示的位置。
3.2. Step 2
-
找到主成分的比例 |估计 ∑^(-1)
第二个组成部分涉及拉伸图形,这是通过 Sigma^-1 步骤实现的。此步骤使用数据中的 sigma 1 和 sigma 2 的方差,类似于 PCA 中使用的方法。
3.3. Step 3
-
旋转的独立性和峰度假设 |估计 V
将当前算法与 PCA 区分开来的最后一个组成部分涉及信号围绕角度 Phi 的旋转。此步骤旨在通过利用旋转的独立性和峰度假设来重建信号的原始维度。
总之,该算法采用测量并围绕 theta 执行旋转,通过使用方差 sigma 1 和 2 进行拉伸,最后围绕 Phi 旋转。以下幻灯片总结了这些步骤的数学背景以供参考。
如您所见,我们可以仅使用两个角度和数据的方差来确定逆矩阵 A,这实际上是我们处理 ICA 算法所需的全部。进行测量、旋转和缩放它们。最后,我们再次旋转它们以获得最终尺寸。
4. 代码
我希望你到目前为止已经理解了 ICA 算法的基本思想。没有必要从数学上理解每一步,但有助于理解其背后的概念。有了这些知识,我想和你一起做一个实际的例子来展示 ICA 算法的实际应用,使用 R 中一个叫做 fastICA 的函数。
# install fastICA package in R
install.packages("fastICA")
# load required libraries
library(MASS) # To use mvrnorm()
library(fastICA)
我们创建了两个随机数据集:信号 1 和信号 2,可以将其想象为来自我们两个鸡尾酒组的语音信号:
# random data for signal 1
s1=as.numeric(0.7*sin((1:1000)/19+0.57*pi) + mvrnorm(n = 1000, mu = 0, Sigma = 0.004))
plot(s1, col="red", main = "Signal 1", xlab = "Time", ylab = "Amplitude")
# random data for signal 1
s2=as.numeric(sin((1:1000)/33) + mvrnorm(n = 1000, mu = 0.03, Sigma = 0.005))
plot(s2, col="blue", main = "Signal 2",xlab = "Time", ylab = "Amplitude")
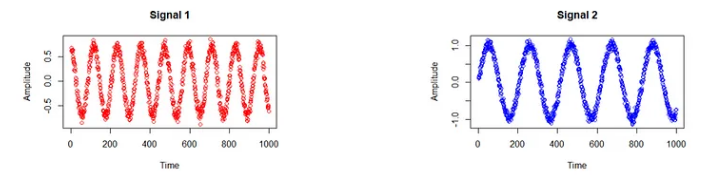
红色曲线代表第一个信号,蓝色曲线代表第二个信号。在这种情况下,形状无关紧要。您应该看到的是这两个信号彼此不同。现在让我们混合它们!
# measurements with mixed data x1 and x2
x1 <- sine1-2*sine2
plot(x1, main = "Linearly Mixed Signal 1", xlab = "Time", ylab = "Amplitude")
x2 <- 1.73*sine1 +3.41*sine2
plot(x2, main = "Linearly Mixed Signal 2", xlab = "Time", ylab = "Amplitude")
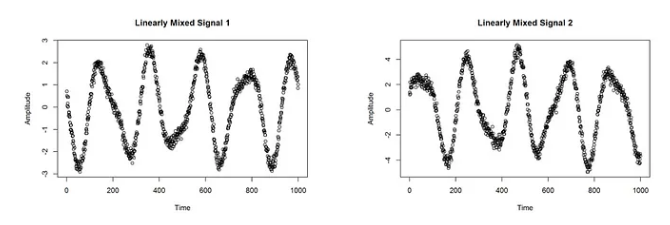
正如您在上面看到的,我们使用两个信号模拟了两个测量。因此,测量中的信号不再独立。两种混合信号都可以想象成鸡尾酒示例中两个麦克风的录音。我们现在忘记我们的两个原始信号并想象,这两个测量值是我们拥有的关于该数据的唯一信息。
因此我们想将它们分开,最终得到两个独立的信号:
# apply fastICA function to identify independent signals
measurements <- t(rbind(x1,x2))
estimation <- fastICA(measurements, 2, alg.typ = "parallel", fun = "logcosh", alpha = 1, method = "C", row.norm = FALSE, maxit = 200, tol = 0.0001, verbose = TRUE)
plot(estimation$S[,1], col="red", main = "Estimated signals", xlab = "Time", ylab = "Amplitude")
lines(estimation$S[,2], col="blue")
mtext("Signal 1 estimation in red, Signal 2 estimation in blue")
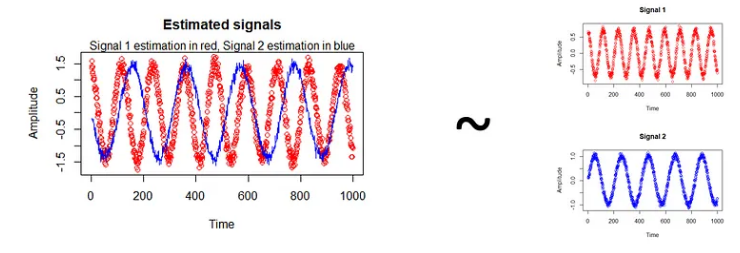
该算法的结果如上所示。红色曲线是信号 1 的估计值,而蓝色曲线是信号 2 的估计值。毫不奇怪,该算法几乎估计了原始信号,如右图所示。您可能已经注意到,红色曲线与预期完全吻合,而蓝色曲线似乎是倒转的。这是因为该算法无法恢复源活动的确切幅度。但除此之外,这里的重建工作做得非常好。
总结
-
优点
ICA 只能分离线性混合源,而且我们无法完美分离高斯分布的源,因为它们会终止我们算法的第三步。虽然我们期望独立源混合在线性组合中,但 ICA 会找到一个空间,即使是非独立源也能最大限度地独立。
-
缺点
ICA 算法是一种适用于不同领域的强大方法,并且很容易在 R 的开源包中使用; Mathlab 和其他系统。 ICA 算法用于应用程序的示例有很多:人脸识别应用程序、股票市场预测等等。因此,它在实际使用中是一种重要且备受推崇的方法。
参考资料
Source: https://towardsdatascience.com/introduction-to-ica-independent-component-analysis-b2c3c4720cd9
本文由 mdnice 多平台发布