目录

23、合并K个升序链表

32、最长有效括号

 33、搜索旋转排序数组

---

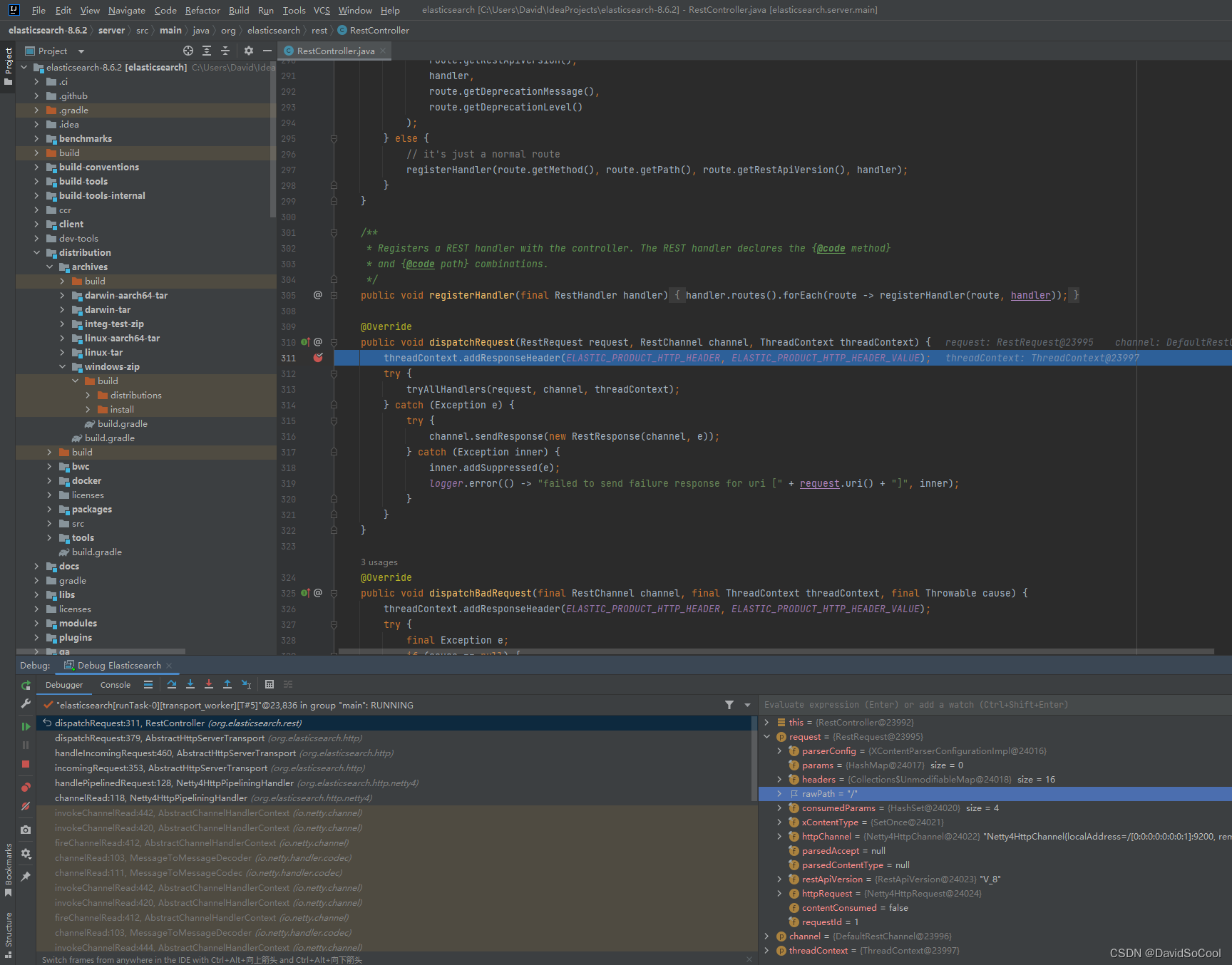
23、合并K个升序链表

思路：采用顺序合并的方法，用一个变量 ans 来维护以及合并的链表，第 i 次循i 个链表和 ans合并，答案保存到 ans中。

代码： 

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] listNodes){
        ListNode ans = null;
        for (int i = 0; i < listNodes.length; i++) {
            ans = mergeTwoLists(ans,listNodes[i]);
        }
        
        return ans;
    }

    public ListNode mergeTwoLists(ListNode a, ListNode b){
        //当有一个为空时，就返回另一个链表
        if (a == null || b == null){
            return a != null ? a : b;
        }

        //创建虚拟头结点的临时链表
        ListNode head = new ListNode(0);
        ListNode tail = head;
        ListNode aPtr = a;
        ListNode bPtr = b;

        while (aPtr != null && bPtr != null){
            if (aPtr.val < bPtr.val) {
                tail.next = aPtr;
                aPtr = aPtr.next;
            } else {
                tail.next = bPtr;
                bPtr = bPtr.next;
            }

            tail = tail.next;

        }

        tail.next = (aPtr!=null ? aPtr : bPtr);

        return head.next;


    }
}

32、最长有效括号

思路：借助栈，遇到的每个 ‘(’，我们将它的下标放入栈中，对于遇到的每个 ‘)’，我们先弹出栈顶元素表示匹配了当前右括号。

• 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
• 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度。

代码：

class Solution {
    public int longestValidParentheses(String s) {
            //最大长度
            int maxans = 0;
            Stack<Integer> stack = new Stack<>();
            //首先弹入一个虚拟下标，防止出现第一个即为')'而需要分类讨论的情况
            stack.push(-1);
            for (int i = 0; i < s.length(); i++) {
                if (s.charAt(i) == '(') {
                    stack.push(i);
                } else {
                    stack.pop();
                    if (stack.isEmpty()) {
                        stack.push(i);
                    } else {
                        maxans = Math.max(maxans, i - stack.peek());
                    }
                }
            }
            return maxans;
        }
}

 33、搜索旋转排序数组

 

思路：使用二分查找（双指针）。我们将数组从中间分开成左右两部分的时候，一定有一部分的数组是有序的。例如，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

• 如果[1，mid - 1]是有序数组，且target 的大小满足[nums[], nums[mid)， 则我们应该将搜索范围缩小至[1， mid一1]，否则在[mid + 1，r]中寻找。
• 如果[mid, r] 是有序数组，且target 的大小满足(nums[mid + 1], nums[r1]，则我们应该将搜索范围缩小至[mid + 1，r],否则在[1，mid - 1] 中寻找。

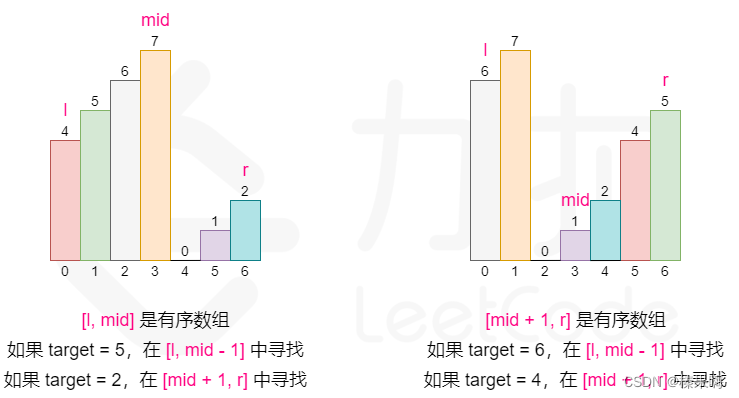
 （图源自leetcode）

代码：

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        //数组为空时
        if (n == 0) {
            return -1;
        }
        //数组长度为1时
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {
                return mid;
            }
            //如果此时数组有序，双指针收缩
            if (nums[0] <= nums[mid]) {
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {        //如果此时无序，则另一半一定是有序的
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
}