关于存储的几个概念

对于一个存储系统来说，底层的存储结构基本上就决定了这个存储系统的功能，或者说性能偏向。比如

使用B+树的存储系统，那就是查询友好的；

使用倒排索引结构的，那就主要是用来做全文搜索的；

使用key-value结构的，在分布式系统中，nosql基本上都是采用了key-value来存储的，这类系统往往是偏向于等值查询，比如缓存等场景。但是在newsql发展中，计算和存储分离后，底层的存储好多都是采用key-value的存储，然后再次基础之上，叠加一个计算组件，来满足二维表的结构化数据的查询和维护。

对于一个存储系统来说，肯定不会是单一的数据结构就能够满足要求的，上面列出出来的，只是说一个特定偏向领域的存储系统主要的这种数据结构，比如mysql的数据是以B+树来组织的，但并不表示mysql的实现里没有用到hash表、跳表等等呢个数据结构。

不过这里需要单独说一下的是，LSM-Tree，也是本文重点会去讨论的，这个虽然叫xxx-Tree，我觉得它和二叉树、红黑树等等这种数据结构还是有本质的差别，LSM-Tree不是一个树结构，而是一种实现数据存储的工程方式，通过一些工程手段来解决读写放大的问题，但是其背后的数据结构可以上任何一种现有的数据结构。

另外，其实还有一个概念非常容易混淆，就是存储方式(数据的组织方式)，这个在讨论OLTP、OLAP的时候，一定会讨论到。和这些概念揉到一起，比较容易混淆。

行存 vs 列存

为了解释清楚，我们以逻辑结构是二维表来举例，就可以一目了然了，比如有如下一张二维表数据(逻辑结构)：

列式存储：数据在存储介质中是按照列来组织的。

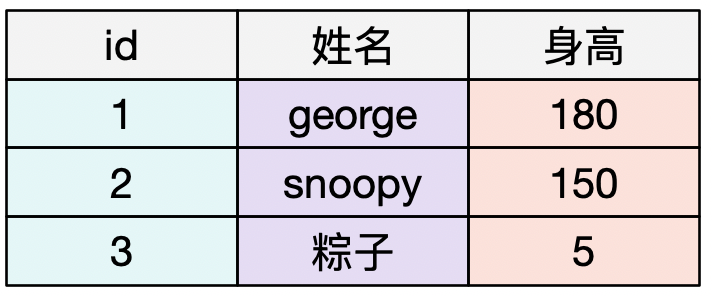
通俗点来说就是将一列的数据进行连续存储，即id这这一列的数据都是连续存放的、姓名这一列的数据也是连续存放的(即geoge、snoopy、粽子这三个值在磁盘上是连续存放在一起的，当然也可能按列的范围进行拆分，所以不一定是一列所有的数据都是连续存放的，得看具体的实现)。对于OLAP场景，其实往往是要将一列或者几列的数据全部取出来，然后就这一列/几列数据进行分析，所以列式存储对于OLAP分析场景，就比较有又是。

行式存储：数据在存储介质中是按照行来组织的。

也就是说子啊存储介质中，会将id=1的这一行(1、geoge、180)数据进行连续存储、将id=2的这一行进行连续存储，依次类推。在OLTP场景中，一行数据往往存储了一个实体的一类数据，比如上述例子就是一行代表了一个人员的进本信息。在OLTP场景中，都是面向一个或者一个范围内的实体进行操作，所以往往会将一个实体的很多数据都查出来，那这种按行组织的方式对这种场景就很友好，不用随机IO/随机内存操作到处去找数据，然后才能将一行数据给组装完。

所以说行存还是列存，指的是数据在存储介质中的是按照逻辑行、还是逻辑列来连续存储的。所以行存和列存根给用户是否以表格的形式展示，没有任何关系(mysql是行存、hbase是列存，但会发现都可以给用户以二维表的方式来展示数据)

这里说明出了二维表的逻辑结构和行存/列存的关系后，其实还有一个概念和表比较容易混淆，顺便这简单说一下，那就是：结构化和非结构化。

结构化 vs 非结构化

要说清楚这个问题，只需要回到一个问题就清楚了，这也是以前一直困扰我的问题：我们说mysql是结构化的存储，它的结构化体现在哪儿？ES存储的是非结构化的数据，但是使用上看一样的有：document、field这些，感觉跟二维表没有任何区别，那么为啥说它存储的是非结构化的信息。

总结到一句话就是：是否结构化，跟给用户展示的逻辑结构、以及数据模型没有任何关系(不管他是不是有行、字段这些概念)，就看一个：是否有一个模式来约束数据。

比如mysql，我们首先就是先创建一张表，其实创建表就是创建了一个约束数据的模式(schema)，后续往mysql里写入数据，就只能按照这个模式的约束来写入，不满足约束，就不允许写入。而这个模式，我个人理解就是在定义数据的结构，那么根据这个模式落下去的数据，自然是满足这个模式定义的结构约束的。

比如，如果我定义了一张表有id、姓名、身高、胸毛，那么这个表里存放的任何数据，都必须有这几个字段，哪怕是george、snoopy和粽子都没有尾巴，但由于schema定义了这个字段，我们就不得不给这个字段一个值(哪怕是null值，也得给它一个值)，否则就不满足schema结构约束。

再看ES(hbase也是一样的)，虽然Lucene在给用户的api中，一样是将数据建模成了：Document、Field的概念，但是一个document里到底可以有哪些字段、字段的类型是什么，这个是没有任何约束的，可以随便在Document里增加、减少。但是对于非结构化，就不一样了，没有就不需要就好了，注意哦，不是没有值，是连这个字段都没有，这是两个概念。也就是说，documentId=1/2/3是没有尾巴这个字段的，是连字段都没有，不是这个字段取值为null。

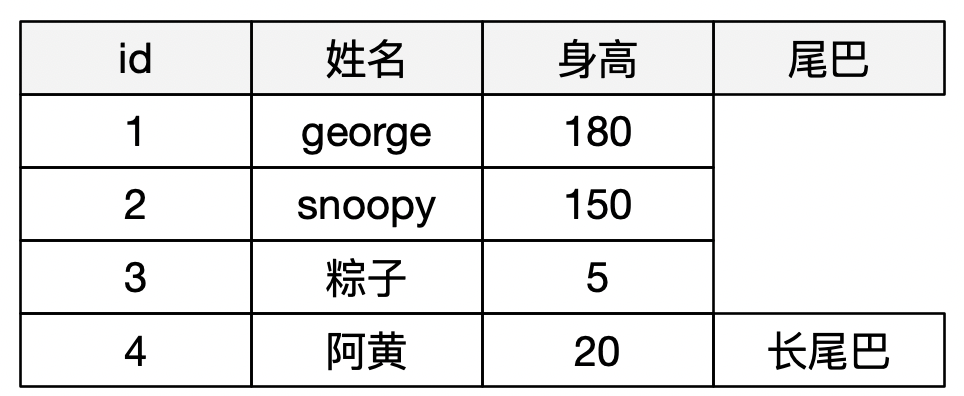
所以，当你使用ES的时候，你会发现，ES里都没有null这个特殊值，它给的查询接口里面，只有exits，根本就么有判断一个字段是否是null，但mysql里对null的判断是有特殊语法的：is null/is not null。

到这，几个概念性的东西都解释过了，接下来就进入正题：阐述一下B+树和LSM-Tree

B+树

B+树本质上是一个平衡的m-n树，其中m是指一个节点里能够存放的数据个数，n是指指向叶子节点的指正个数。其中+的意思就是同层节点是从小到大排序的，且有指向右兄弟的指正(换句话说，同层节点是一个从小到大排序的链表)，下图就是一个B+树(2-3树)。

在B+树中，对范围查找非常友好，比如要等值查询，id=9的数据。

首先就从根节点判断，9是小于40的(如果m更大，那么在节点内部就是一个二分查找，目标值在哪个区间里)，所以去最左指正的指向的子树中继续查找。

到了子树上，发现9是小于10的(m较大的时候就是个二分查找)，然后继续到最左指正指向的节点

发现是叶子节点，且值是0，所以就向右遍历，一直遍历到id=9，则找到对应的数据。

如果是范围查找9<=id<10，那么遍历到id=9的时候，继续往后遍历，发现15是大于10的，所以结果集中也就只有id=9的数据；

如果9<=id<20，同样的继续向右遍历，遍历到id=15、id=40，发现已经比右边界大了，所以收集到结果是id=9和15的数据。

如果是id<20，同样的使用树定位到倒数第二层的(10,15)，那么就会利用mptr找到id=15的叶子节点，开始向右遍历。

总结起来，B+树的查找分为三部分：

节点内的二分查找

非叶子节点树的遍历查找

叶子节点链表的遍历查找

所以B+树的查询其实是hi比较高效的，二分查找和树查找的效率都是O(logN)，而最后的叶子节点遍历虽然是个O(N)的操作，但实际上，只要遍历到不满足条件的节点，就会终止。所以对于一些OLTP的业务，其实更多的是等值或者少量数据的查询，所以B+树的查询效率是非常高的。但也需要注意，对于大批量的数据扫描，那其实就是遍历整个叶子节点链表了，这个效率就会比较低，比如Id>1，那基本就是全表扫描。所以对于用B+树作为存储引擎的数据结构的时候，对于大量数据的扫描其实也不是很友好，直接会全表遍历的。

再来看写入，写入的时候的一个最大的成本就是要维护B+树的结构：

节点内数据是有序的

子树里维护的数据，要满足非叶子节点维护数据的范围。

同层节点，要是排序的。

因为要维护这些结构，所以就会存在额外的数据写入，即写放大问题。比如要插入一个35的节点，

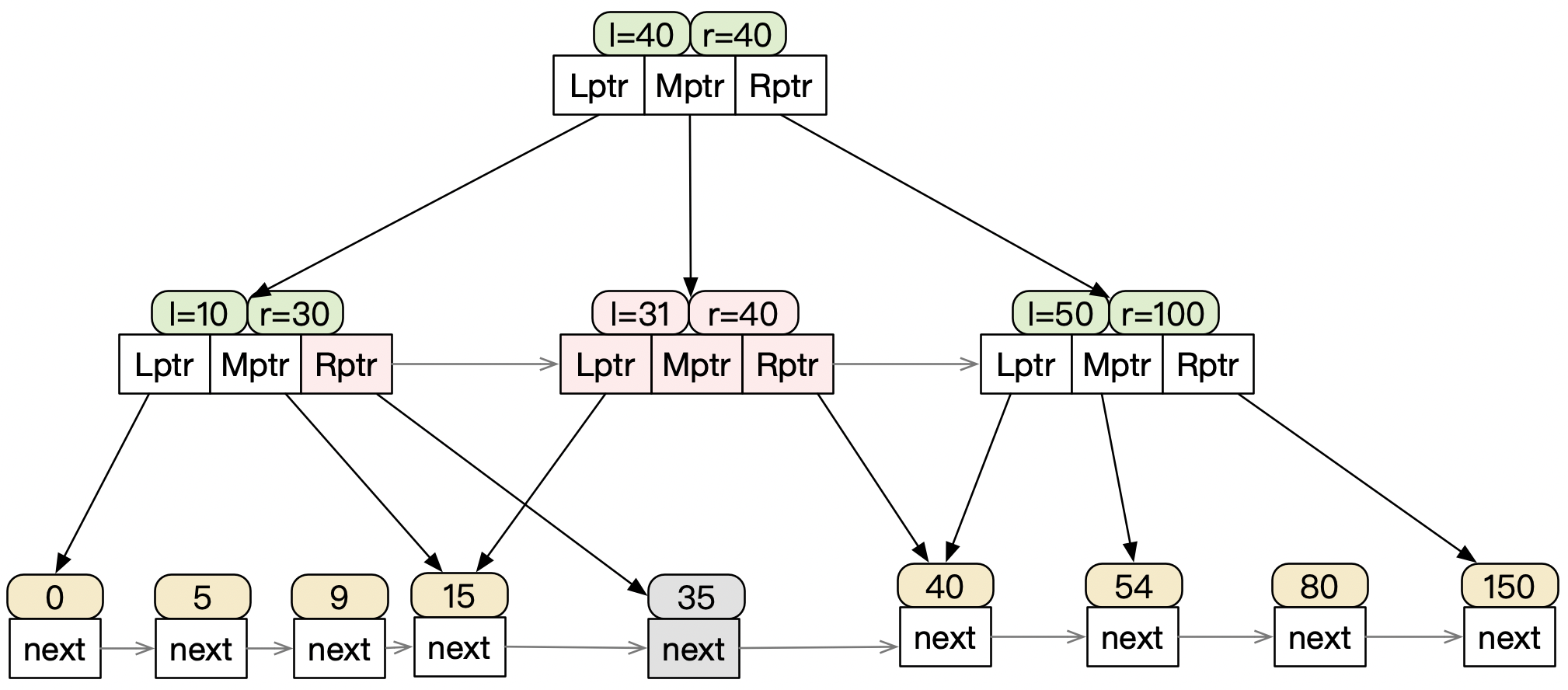
除了会插入35这个叶子节点外，还有额外的一个中间节点指针的修改，以及新增了一个中间节点，为了数据的均衡，其实还可能修改原有叶子节点里的数据的范围，那就会进一步放大写入操作。

另外在mysql的实现中，哪怕是叶子节点，也不是一个节点只是存储一条数据，而是以page为单位，一个page里存放了多条数据(按索引排序的多条数据，主键索引就是按主键排序、辅助索引就是按照辅助索引排序的)，那么对于mysql来讲，其实还多了页内数据的维护。而且mysql的page的大小是固定的，所以在写入数据的时候，为了保证页内数据的有序性，以及同层page之间的有序性，那在写入一条数据的时候，就有可能出现页分裂的问题。比如按page组织的叶子节点如下，要插入数据8

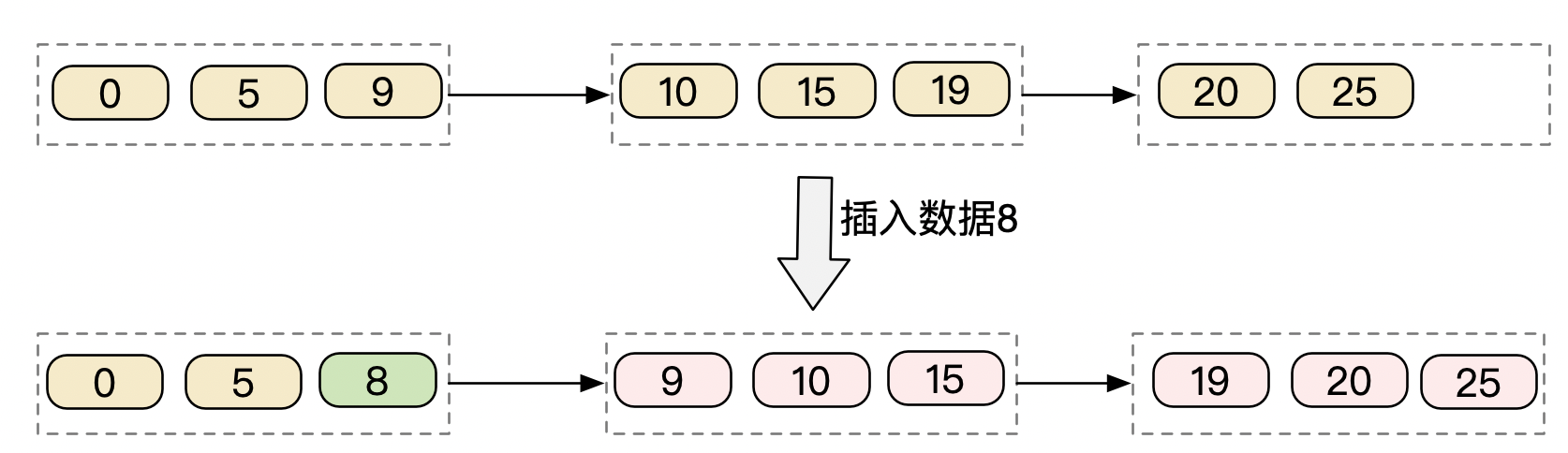
其实三个page都需要重新写入的，想下如果数据量很大的时候，本来只是想插入一个数据，那所有的page都需要修改一下，那这个效率是会有多慢。所以在mysql的使用中，也是建议使用递增的主键，以避免主键索引树发生页分裂的问题。而mysql内存中的page和磁盘中的page是对应的，那么也就是说，这里所有的page都需要刷一次磁盘。

衡量写放大问题有个写放大系数（Write Amplification Factor，WAF）就是来衡量写放大的一个指标，它指实际写入磁盘的数据量和应用程序要求写入数据量之比。比如上述的例子WAF=100kb/1kb=100。

对于写放大的的优化方式，常见的方式就是：预留填充，基本思路就是在page中预留一些空间，这样不会因为少量的数据写入造成树结构的大幅变动。但是到底预留多大就是个问题：

过大则无法解决写放大问题；

过小会造成页表数量膨胀，增大对磁盘的扫描范围，降低查询性能

B+树的另外一个问题就是实际存储是不连续的，也就是说在逻辑结构上，同层节点是链表结构，通过指正链接到一起，但实际上，各个page存储到磁盘，不是连续空间存放的，所以这种不连续的存储就会导致查询的时候寻址成本的增加。

在一个存储系统中，关于读、写、空间三个方面的优化中，有一个RUM猜想：对任何数据结构来说，在Read Overhead（读）、Update Overhead（写）和Memoryor Storage Overhead（存储）中，同时优化两项时，需要以另一项劣化作为代价。

这跟分布式系统的CAP理论一样，在一个存储系统中，就需要权限读、写、占用空间之间的一个权衡。

LSM-Tree

B+树作为存储引擎的结构时候，由于存在写放大、和存储的不连续的问题，所以一些新兴的存储型的组件，开始采用LSM-Tree(Log Structured-MergeTree)来作为底层的存储结构，比如很多分布式数据库，如TiDb、OceanBase等，以及ES的新版本的数据存储也开始采用LSM-Tree了。

首先需要明确一点，LSM-Tree是google提出来的，虽然它的名字里有个tree，但它不是一个数据结构里的那个树。其核心在于前面的LSM：Log Structured-Merge

LSM-Tree的核心思想是将数据的写入分成了两部分：内存部分和磁盘部分。写入过程：

首先写入内存的memTable，以及wal日志，写入就直接返回了。所以正常情况下，写入操作会非常的快。只是涉及一个内存操作和一个磁盘的顺序写操作。

当memTable达到一定的阈值的时候。就会将memTable flush到磁盘中。

新创建一个memTable，使用新的memTable来服务新的写入请求。

原来的memTable就变成了imutable memTable。然后将imutable memTable中的数据进行整理：按照key进行排序。

将排序后的imutable memTable直接刷到磁盘，在磁盘里对应的就是SStable。所以，在磁盘中，会不断新增SStable。

随着系统的运行SStable越来越多，这个时候就会按照一定的规则对SStable进行compact整理合并。

通过整个写入过程会发现，会发现其实LSM-Tree不是没有写放大，而是将写放大的过程给转移了，转移到compact过程了。

所以，LSM-Tree的写放大指数，就看compact过程的合并策略了。

Size-Tiered Compact Strategy合并策略

Size-Tiered Compact Strategy，简称Tiered，其基本能思想就是每当某个尺寸的SSTable数量达到既定个数时，将所有SSTable合并成一个大的SSTable。这种策略的优点是比较直观，实现简单，但是缺点也很突出

Tiered合并策略的读放大问题

SSTable文件是按照时间间隔产生的，所以在不同的SSTable文件中，就有可能存在相同的key的数据。所以每次读取的时候，都需要遍历所有的SSTable，然后合并key的值后，才能确定某个key的最终取值是什么。

SSTable内部是按照Key排序的，所以查找方法可以是二分查找，所以查找单个SSTable的时间复杂度是O(logN)，其中N是SSTable中key的个数。有M个SSTable，整体时间复杂度就是O(MlogN)。当然执行Compact后，读的复杂度会有所下降，因为SSTable的文件减少了。

当然也可以发现，如果系统中只有一个SSTable的时候，其实是没有读放大的。

Tiered合并策略的写放大问题

Compact后会减少SStable的个数，从而降低读放大。但是Compact过程会带来更多的写放大和空间放大。

通过LSM-Tree的写入过程会发现，LSM-Tree不是没有写放大问题，而是将将写放大转移了，只是说在实际写入操作的时候没有写放大，从而可以承载大量的并发写入。

但如果持续写入，产生大量的SStable，就会执行Comapct过程，而Compact过程就会有比较大的I/O开销、内存、cpu的开销。而Tiered合并策略是在Compact的过程，会合并当前系统中的所有SSTable，所以相比于B+树写入时候的写放大成本，总体上Tiered合并策略在Compact时的成本可能会更大。而且由于Compact会占用I/O、cpu等资源，其实反过来就会可能影响写入操作以及读操作。

Tiered合并策略的空间放大问题

从空间放大的角度看，Tiered策略需要分别存储合并前的多个SSTable和合并后的一个SSTable，所以需要两倍于数据大小的空间。所以空间放大指数(SAF)就是2，而B+树的SAF是1.33.

一通分析过后，LSM-Tree只是在短时间内写入速度快以外，还存在更多的读放大、写放大、空间放大的问题，而且Compact时会耗费大量的I/O的资源，反过来还会影响读写操作，看起来比B+树没有什么优势。

其实这些问题只是Tiered合并策略的问题，LSM-Tree的核心优势在于另外一个合并策略：Leveled Compact Strategy合并策略，这个合并策略将有效的解决这些问题

Leveled Compact Strategy合并策略

Tiered策略之所以有严重的写放大和空间放大问题，根问问题是因为每次Compact需要全量SSTable参与，开销自然就很大。

那么如果每次Compact的时候都只是部分SSTable参与，那么Compact过程的写放大和空间放大的问题就能够缓解。

Leveled合并策略的主要思想就是在Compact的时候，只是合并部分SSTable。它将SSTable进行了分层。

将数据分成一系列Key互不重叠且固定大小的SSTable文件，并分层（Level）管理

同时，系统记录每个SSTable文件存储的Key的范围。

LSM-Tree的核心思想是将数据的写入分成了两部分：内存部分和磁盘部分。写入过程：

首先写入内存的memTable，以及wal日志，写入就直接返回了。所以正常情况下，写入操作会非常的快。只是涉及一个内存操作和一个磁盘的顺序写操作。

当memTable达到一定的阈值的时候。就会将memTable flush到磁盘中。

新创建一个memTable，使用新的memTable来服务新的写入请求。

原来的memTable就变成了imutable memTable。然后将imutable memTable中的数据进行整理：按照key进行排序。

将排序后的imutable memTable直接刷到磁盘，在磁盘里对应的就是SStable。所以，在磁盘中，会不断新增SStable。这种直接由imutable memTable刷盘得到的SStable称为L0 SStable。L0 SStable也是按照时间生成的，只是按照key进行了排序，不会去做重复key的整理，所以L0 SStable中也是有重复的交叉key的。这么做的目的就是为了权衡flush效率，

随着系统的运行L0层的SStable越来越，系统中就会存在很多L0 SStable对应的很多小文件。这个时候就会按照一定的规则多(一般系统都会支持一层SStable数量和大小的策略)对L0层的SStable进行compact合并：将所有L0 SStable中的key进行排序、去重合并后，形成一个更大的L1 SStable，然后删除L0的SStable。因为L1 SStable生成的时候会有key的重复整理，L1中的各个SStable中的key都不是重复的。

另外就是在后续的L0 SStable compact过程中，还会结合现有的L1 SStable的情况，进行数据的均衡处理，让数据尽量均匀分散到各个L1 SStable中。

当L1 SStable越来越多的时候，还会继续将L1 SStable进行整理合并成L2 SStable。因为L1中各个SStable中的key是没有重复的，所以compact的时候是没必要所有的L1 SStable都参与，只是合并整理部分就好了，这样主要是可以减少单次compact的I/O等的开销。

Leveled策略的读放大

其实相比于Tired compact策略，Leveled策略并没有减少多少读放大。SStable依然是按照key有序的，那么读取的时候，如果有M个SSTable，每个SSTable文件中有N个key，那么复杂度依然是O(MLgo(N))

但是在实际实现的时候，会有一些优化措施：Leveled会有一个类似于协调节点的角色，来记录每个SStable的meta信息，比如该SStable中保存的key的范围，读取的时候通过这份meta数据，就可以精准的去对应的SStable找到对应的key的数据。而实际实现这个meta数据，可能就是给每个SStable维护一个BloomFilter过滤器，来快速获取某个key是否在该SSTable中存在。

但是需要注意的是，L0 SStable，因为有key的交叉，在读取数据的时候是分两步：