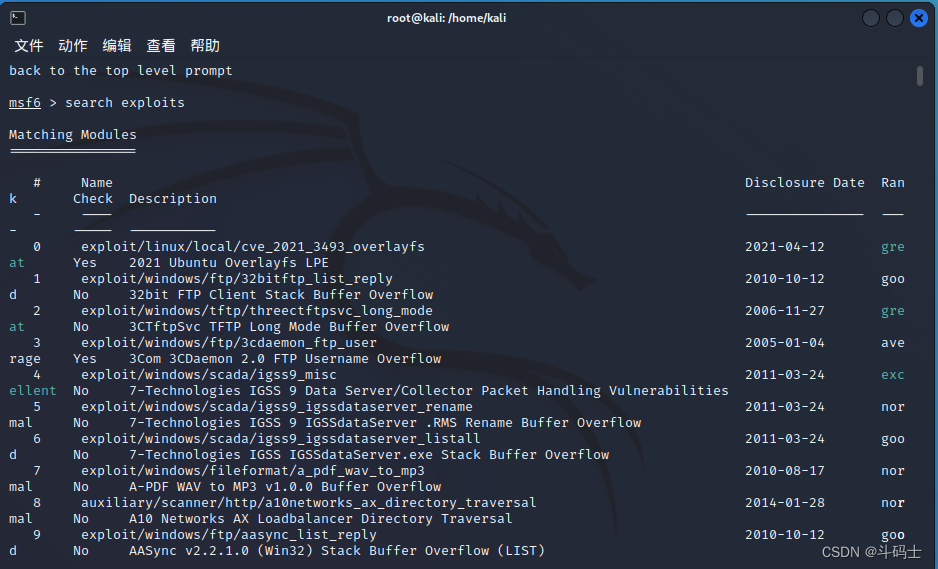
目录
- 基于Graph-Propagation的相关性学习AAAI2020
- 基于graph的高阶关系发现CVPR2021
基于Graph-Propagation的相关性学习AAAI2020
来源:Graph-Propagation Based Correlation Learning for Weakly Supervised Fine-Grained Image Classification(这或许是第一个用graph处理判别区空间关系的FGIA方法)
弱监督细粒度图像分类(WFGIC)的关键是如何挑选出判别区并从中学习判别特征。然而,目前大多数的WFGIC方法都是独立挑选出判别区,直接利用其特征,而忽略了区域特征之间的语义相互关联,区域组具有更强的判别能力。为了解决这些问题,作者提出了一个基于图传播的端到端相关性学习模型GCL,以充分挖掘和利用WFGIC的区域相关的判别潜力。

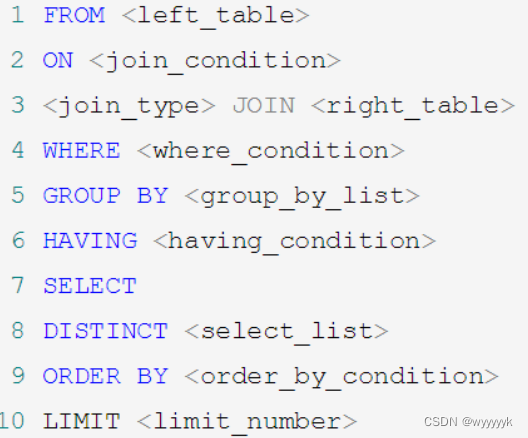
- GCL的动机。a为原始图像,b和d为判别区的打分图,c和e为不使用交叉图传播模块(CGP)和使用交叉图传播模块的定位结果,f和g为未进行相关特征强化学习(CFS)和进行相关特征强化学习的特征向量。
从细粒度图像中学习判别区位置是WFGIC的关键。最近大部分工作分为两组:
- 基于启发式方案的判别区定位,这种方法的局限在于,很难保证所选区域具有足够判别性;
- 基于ML的端到端定位判别区,但是过去的方法比如NTS-Net仅独立对待判别区,忽略了判别区之间的联系。
作者认为挖掘区域间的相关性比单个区域的判别能力更强,这促使作者将判别区之间的相关性纳入管道。

- 基于图传播的相关性学习(GCL)模型的框架。通过纵横交叉图传播(CGP)子网络生成判别邻接矩阵(AM),通过评分网络(Sample)生成判别评分图(score map)。然后GCL根据判别评分图从默认patch(DP)中选择判别性更强的patch。同时,对原始图像进行裁剪和调整,大小为 224 × 224,并通过相关特征增强(CFS)子网络的图传播生成判别特征。最后,将多个特征连接起来,得到WFGIC的最终特征表示。
基于graph的高阶关系发现CVPR2021
来源:Graph-based High-Order Relation Discovery for Fine-grained Recognition
细粒度识别旨在学习有效的特征,以识别视觉上相似对象之间的细微差异。现有工作在复杂背景下表现不稳定,不同语义特征之间的内在关系也没有充分讨论。因此,作者提出一种基于图的关系发现方法,以建立对高阶关系的理解。
细粒度对象识别侧重于将一个基本类别的对象区分为子类,由于不同类别之间存在细微的视觉差异,这在深度学习领域依然是一个挑战。作者在这个问题上结合了判别区学习和特征表示学习(见细粒度视觉分析综述TPAMI2021中,基于定位子网络的识别和端到端特征编码)
- 对于判别区学习:通过提取part(局部化)来处理细粒度分类问题。一些有代表性的方法倾向于在分类任务中使用part检测器]或分割器。在获得准确的part解析结果的同时,细粒度分类器也能获得令人满意的性能。除了使用额外手动标注的方法外,基于注意力的方法在弱监督训练中显示了发现目标part的能力。然而,使用注意力机制的part在复杂背景下往往会得到不可靠的结果,由于网络无法捕获正确的part,进一步加强这些区域将导致灾难性的过拟合。
- 对于端到端特征编码:通常将分类问题作为表示学习任务来处理,由于在弱监督分类任务中,对象的part自然出现在不同的feature map通道中,因此利用不同通道之间的关系对于细粒度的特征表示是有益的。作为主要的方法之一,bilinear pooling利用了来自两个不同网络的二阶分类特征。但注意,高阶特征引入高维数,严重加大计算量。
因此,作者思考:如何利用高阶关系改善part的感知,如何将高阶关系表示到低维。
bilinear pooling来自Bilinear CNN Models for Fine-grained Visual Recognition:
图像输入两个特征提取器,对于图像 L L L在位置 l l l的两个特征 f A ( l , L ) ∈ R 1 × M f_{A}(l,L)\in R^{1\times M} fA(l,L)∈R1×M和 f B ( l , L ) ∈ R 1 × N f_{B}(l,L)\in R^{1\times N} fB(l,L)∈R1×N, M M M和 N N N分别为通道数,进行如下操作: b ( l , L , f A , f B ) = f A T ( l , L ) f B ( l , L ) ∈ R M × N b(l,L,f_{A},f_{B})=f_{A}^{T}(l,L)f_{B}(l,L)\in R^{M\times N} b(l,L,fA,fB)=fAT(l,L)fB(l,L)∈RM×N注意,对于所有的 L L L个位置有: b ( L , f A , f B ) = f A T ( L ) f B ( L ) ∈ R M × N b(L,f_{A},f_{B})=f_{A}^{T}(L)f_{B}(L)\in R^{M\times N} b(L,fA,fB)=fAT(L)fB(L)∈RM×N因此: δ ( L ) = ∑ l A b ( L , f A , f B ) \delta(L)=\sum_{l}^{A}b(L,f_{A},f_{B}) δ(L)=l∑Ab(L,fA,fB) x = v e c ( δ ( L ) ) x=vec(\delta(L)) x=vec(δ(L)) y = s i g n ( x ) ∣ x ∣ y=sign(x)\sqrt{|x|} y=sign(x)∣x∣ z = y / ∣ ∣ y ∣ ∣ 2 z=y/||y||_{2} z=y/∣∣y∣∣2
直观上理解,bilinear pooling先把在同一位置上的两个特征双线性融合(相乘)后,得到矩阵 b b b,然后将矩阵 b b b sum pooling得到矩阵 δ \delta δ,最后把矩阵 δ \delta δ reshape为向量,进行归一化操作后得到融合特征 z z z,该特征用于细粒度分类。
如果特征来自两个不同的特征提取器,则被称为多模双线性池化(MBP,Multimodal Bilinear Pooling);如果特征来自同一个提取器,则被称为同源双线性池化(HBP,Homogeneous Bilinear Pooling)或者二阶池化(Second-order Pooling)。
作者提出一种基于图的关系发现方法(GaRD,graph-based relation discovery),用于细粒度识别。第一个关键思想是利用不同语义通道之间的相互关系。由于这些特征是灾难性的高维特征,通常难以优化,作者提出了一个新的基于图的语义分组模块,将这些特征嵌入到紧凑空间中。除了这些改进之外,作者提出了一种分组学习策略来缓解梯度下降优化中的异常值。

- GaRD由三个基本模块组成:关系发现模块提取丰富的关系感知高维特征,基于图的语义分组模块查找低维特征嵌入,采用分组学习策略使用类中心更新梯度。