决策树的基本原理
决策树是⼀种分⽽治之的决策过程。⼀个困难的预测问题,通过树的分⽀节点,被划分成两个或多个较为简单的⼦集,从结构上划分为不同的⼦问题。将依规则分割数据集的过程不断递归下去。随着树的深度不断增加,分⽀节点的⼦集越来越⼩,所需要提的问题数也逐渐简化。当分⽀节点的深度或者问题的简单程度满⾜⼀定的停⽌规则时, 该分⽀节点会停⽌分裂。
决策树是一种自上而下,对样本数据进行树形分类的过程,由结点和有向边组成。结点分为内部节点和叶结点,其中内部结点表示一个特征或属性,叶结点表示类别。从顶部根节点开始,所有样本聚在一起。经过根结点的划分,样本别分到不同的子结点中。在根据子结点的特征进一步划分,直至所有样本都被归到某一个类别(即叶结点)中。
- 优点:不需要任何领域知识或参数假设;适合⾼维数据;短时间内处理⼤量数据,得到可⾏且效果较好的结果;能够同时处理数据型和常规性属性。
- 缺点:对于各类别样本数量不⼀致数据,信息增益偏向于那些具有更多数值的特征;易于过拟合;忽略属性之间的相关性;不⽀持在线学习。
决策树的三要素
一般而言,决策树的生成包括特征选择、树的构造、树的剪枝三个过程。
- 特征选择:从训练数据中众多的特征中选择⼀个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准,从⽽衍⽣出不同的决策树算法。
- 决策树⽣成:根据选择的特征评估标准,从上⾄下递归地⽣成⼦节点,直到数据集不可分则决策树停⽌⽣长。树结构来说,递归结构是最容易理解的⽅式。
- 剪枝:决策树容易过拟合,⼀般来需要剪枝,缩⼩树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
决策树学习基本算法

熵与信息增益
熵
熵可以表⽰样本集合的不确定性,熵越⼤,样本的不确定性就越⼤。
假设随机变量X的可能取值有x1,x2, …, xn,对于每⼀个可能的取值xi,其概率为:
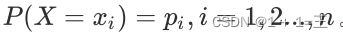
随机变量的熵为:
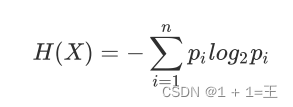
对于样本集合,假设样本有k个类别,每个类别的概率为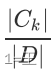 其中|Ck|为类别为k的样本个数, |D| 为样本总数。样本集合D的熵为:
其中|Ck|为类别为k的样本个数, |D| 为样本总数。样本集合D的熵为:
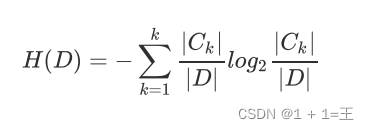
信息增益
假设划分前样本集合D的熵为H(D)。使⽤某个特征A划分数据集D,计算划分后的数据⼦
集的熵为H(D|A),则A特征的信息增益为:
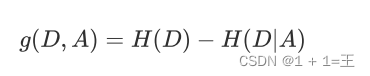
决策树的剪枝方法
剪枝处理是决策树学习算法⽤来解决过拟合问题的⼀种办法。通过对决策树进行剪枝,剪掉一些枝叶,提升模型的泛化能力。决策树的剪枝通常有两种方法:预剪枝(pre-pruning)和后剪枝(post-pruning)。
- 预剪枝:在生成决策树的过程中提前停止树的增长;
- 后剪枝:⽣成决策树以后,再⾃下⽽上对⾮叶结点进⾏剪枝,得到简化版的剪枝决策树。
预剪枝
预剪枝的核心思想是在树中结点进行扩展之前,先计算当前的划分是否能带来模型泛化能力的提升,如果不能,则不再继续生长子树。此时可能存在不同类别的样本同时存于结点中,按照多数投票的原则判断该结点所属类别。预剪枝对于何时停止决策树的生长有以下几种方法。
- 当树到达一定深度的时候,停止树的生长。
- 当到达当前结点的样本数量小于某个阈值的时候,停止树的生长。
- 计算每次分裂对测试集的准确度提升,当小于某个阈值的时候,不再继续扩展。
预剪枝具有思想直接、算法简单、效率高等特点,适合解决大规模问题。但预剪枝存在一定局限性,有欠拟合的风险,虽然当前的划分会导致测试集准确率降低,但在之后的划分中,准确率可能会有显著上升。
后剪枝
后剪枝的核心思想是让算法生成一棵完全生 长的决策树,然后从最底层向上计算是否剪枝。剪枝过程将子树删除,用一个叶子结点替代,该结点的类别同样按照多数投票的原则进行判断。同样地,后剪枝也可以通过在测试集上的准确率进行判断,如果剪枝过后准确率有所提升,则进行剪枝。
相比于预剪枝,后剪枝方法通常可以得到泛化能力更强的决策树,但时间开销会更大。
常见的后剪枝方法包括:错误率降低剪枝( Reduced Error Pruning,REP)、悲观剪枝( Pessimistic Error Pruning, PEP) 、代价复杂度剪枝( Cost Complexity Pruning, CCP )、最小误差剪枝(MinimumEror Pruning, MEP )、CVP(Critical Value Pruning)、OPP (OpttimalPruning)等







![[FI业务流程] - 未清项管理 (XOPVW, XLGCLR, X_UJ_CLR)](https://img-blog.csdnimg.cn/4be26dff66a5413c86fbab66960990c9.png)