1、BN（Batch Normalization）

深度网络参数训练时内部存在协方差偏移（Internal Covariate Shift）现 象：深度网络内部数据分布在训练过程中发生变化的现象。

训练深度网络时，神经网络隐层参数更新会导致网络输出层输出数据的分布 发生变化，而且随着层数的增加，根据链式规则，这种偏移现象会逐渐被放大。 这对于网络参数学习来说是个问题：因为神经网络本质学习的就是数据分布 （representation learning），如果数据分布变化了，神经网络又不得不学习 新的分布。为保证网络参数训练的稳定性和收敛性，往往需要选择比较小的学习 速率（learning rate），同时参数初始化的好坏也明显影响训练出的模型精度， 特别是在训练具有饱和非线性（死区特性）的网络，比如即采用 S 或双 S 激活函 数网络，比如 LSTM，GRU。

因此需要引入 Batch Normalization，作为深度网络模型的一个层，每次先 对 input 数据进行归一化，再送入神经网络输入层。 神经网络的训练过程中，更新了某一层的权重参数，后续每一层网络的输出 都可能发生变化，最终引起 loss 值的变化。所以当没有 BN 层时，loss 的收敛 就需要我们精心设计权重的初始化方法和超参数的调节方法以及等待漫长的训 练时间；但当我们在各层之间加入了 BN 层后，某层的输出仅由两个参数γ和β 决定，使用梯度下降法优化参数时，优化方法只需要调节两个参数的值来控制各 层的输出，而不需要调节各层的全部参数。这样极大地提高了收敛速度，避免了 小心翼翼的参数初始化和超参数调节过程。

Batch normalization 也可以被看做一个层面. 在一层层的添加神经网络 的时候, 我们先有数据 X, 再添加全连接层, 全连接层的计算结果会经过激活 函数成为下一层的输入, 接着重复之前的操作。Batch Normalization (BN) 就 被添加在每一个全连接和激励函数之间。

BN 的作用：

（1）加快网络的训练和收敛的速度； （2）控制梯度爆炸防止梯度消失； （3）防止过拟合。

BN 的缺陷：

（1）高度依赖于 mini-batch 的大小，实际使用中会对 mini-Batch 大小进 行约束，不适合类似在线学习（mini-batch 为 1）。 （2）不适用于 RNN 网络中 normalize 操作：BN 实际使用时需要计算并且保 存某一层神经网络 mini-batch 的均值和方差等统计信息，对于对一个固定深度 的前向神经网络（DNN，CNN）使用 BN，很方便；但对于 RNN 来说，sequence 的长度是不一致的，换句话说 RNN 的深度不是固定的，不同的 time-step 需要保存 不同的 statics 特征，可能存在一个特殊 sequence 比其的 sequence 长很多，这 样 training 时，计算很麻烦。

BN 适用于判别模型，比如图像分类模型，因为 BN 注重对每个 Batch 进行 Normalization 操作，从而保证数据分布的一致性，而判别模型的结果正是取决 于数据整体分布。但是 BN 对 BatchSize 的大小比较敏感，由于每次计算均值和 方差是在一个 Batch 上，所以如果 BatchSize 太小，则计算的均值和方差不足以 代表整个数据分布。

2、IN（Instance normalization）

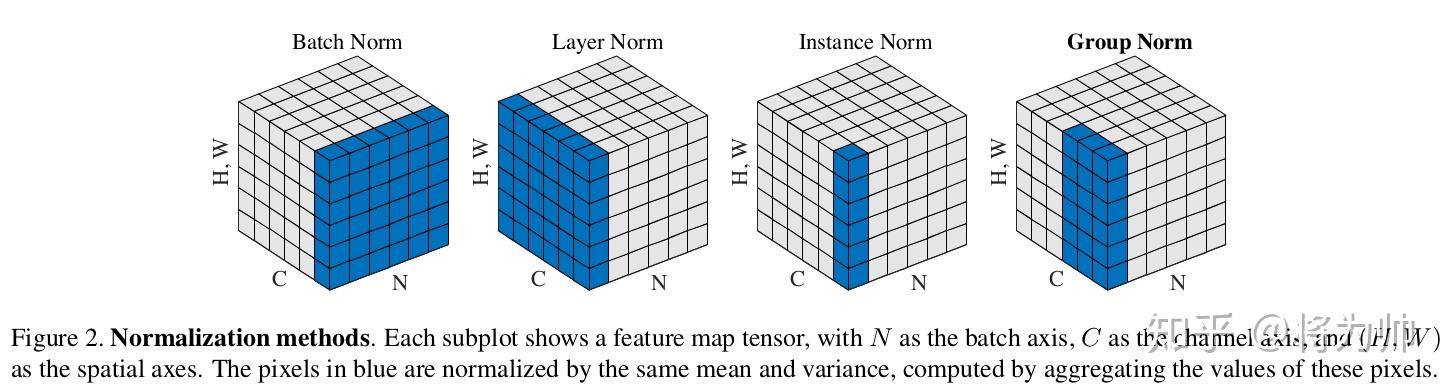
IN 是作用于单张图片，但是 BN 作用于一个 Batch。IN 是针对于不同的 batch, 不同的 chennel 进行归一化。还是把图像的尺寸表示为[N, C, H, W]的话，IN 则是针对于[H,W]进行归一化。

IN 适用于生成模型中，比如图片风格迁移。因为图片生成的结果主要依赖 于某个图像实例，所以对整个 Batch 进行 Normalization 操作并不适合图像风格 化的任务，在风格迁移中适用 IN 不仅可以加速模型收敛，并且可以保持每个图 像实例之间的独立性。

3、LN（Layer Normalization）

BN 并不适用于 RNN 等动态网络和 batchsize 较小的时候效果不好。Layer Normalization（LN）的提出有效的解决 BN 的这两个问题。

Layer Normalization 的基本思想是：用同层隐层神经元的响应值作为集合 S 的范围，来求均值和方差。而 RNN 的每个时间步的都有隐层，且包含了若干神 经元，所以 Layer Normalization 可直接应用于 RNN。

LN 的方法是对于每一个 sample 中的多个 feature(也就是 channel)进行归 一化操作。把图像的尺寸表示为[N, C, H, W]的话，LN 则是对于[C,H,W]进行归 一化。相对于 BN 中所表示的同一个 feature 在不同的 batch 之间拥有同样的均 值和方差。LN 中所表示的则是在同一个 sample 中，不同的 feature 上有着相同 的均值和方差。

4、GN（Group Nomalization）

GN 介于 LN 和 IN 之间，其首先将 channel 分为许多组（group），对每一组 做归一化，及先将 feature 的维度由[N, C, H, W]reshape 为[N, G，C//G , H, W]，归一化的维度为[C//G , H, W] 事实上，GN 的极端情况就是 LN 和 IN，分别对应 G 等于 C 和 G 等于 1，作者 在论文中给出 G 设为 32 较好。

GN 同样可以针对于 mini batch size 较小的情况。因为它有不受 batch size 的约束。 ，LN/IN 和 GN 都没有对 batch 作平均，所以当 batch 变化时，网络的错误 率不会有明显变化。但论文的实验显示：LN 和 IN 在时间序列模型(RNN/LSTM) 和生成模型(GAN)上有很好的效果，而 GN 在视觉模型上表现更好。