🤵‍♂️ 个人主页：@艾派森的个人主页

✍🏻作者简介：Python学习者
🐋 希望大家多多支持，我们一起进步！😄
如果文章对你有帮助的话，
欢迎评论 💬点赞👍🏻 收藏 📂加关注+

---

目录

 推断统计与参数检验

假设检验 

两独立样本t检验 

两独立样本t检验的应用 

---

【SPSS】专栏正在不断更新中，感兴趣的小伙伴可以点个订阅支持一下

SPSS数据分析软件的安装与介绍（附网盘链接）

SPSS连接mysql数据库详细操作教程

【SPSS】数据预处理基础教程（附案例实战）

【SPSS】频数分析和基本描述统计量详细操作教程（附实战案例）

【SPSS】列联表分析详细操作教程（附案例实战）

【SPSS】多选项分析详细操作教程（附案例实战）

【SPSS】单样本T检验分析详细操作教程（附案例实战）

【SPSS】基础图形的绘制（条形图、折线图、饼图、箱图）详细操作过程

 推断统计与参数检验

推断统计

• 推断统计方法是根据样本数据推断总体特征的方法
• 推断统计包括参数估计 (点估计和区间估计)和假设检验两大类 

参数检验 VS 非参数检验

• 参数检验（参数假设检验）

总体分布已知 （如总体为正态分布）的情况下,根据样本数据对总体分布的统计参数(如均值、方差等)进行推断

• 非参数检验（非参数假设检验）

总体分布未知的情况下,根据样本数据对总体的分布形式或数字特征进行推断 

假设检验 

假设检验的基本思想

1 首先，对总体参数值提出假设

2 然后，利用样本告知的信息去验证先前提出的假设是否成立

• 如果样本数据不能够充分证明和支持假设,则应拒绝假设
• 如果样本数据能够充分证明和支持假设,则不能推翻假设 

小概率原理：

• 发生概率很小的随机事件在某一次特定的实验中是几乎不可能发生的
• 小概率原理是假设检验所依据的原理 

假设检验的基本步骤

1.提出原假设(记为H0 )和备择假设(记为H1 ) 通常，将希望推翻的假设放在原假设上

2.选择检验统计量：检验统计量服从或近似服从某种已知的理论分布

3.计算概率P值：在认为原假设成立的条件下,根据样本数据和检验统计量计算 概率P值,该概率值间接地给出了样本值(或更极端值)在原假设成 立条件下发生的概率，即：P(拒绝H0|H0为真) 

4.给定显著性水平α,并作出统计决策：显著性水平α是在原假设H0正确的前提下却拒绝原假设的概率，即“弃真”概率，一般设定为 0.05或0.01 若概率P值小于等于α，拒绝原假设；否则，不能拒绝原假设 

两独立样本t检验 

两独立样本t检验介绍

目的：利用来自两个总体的独立样本,推断两个总体的均值是否存在显著差异

前提：

• 样本来自的总体应服从或近似服从正态分布
• 两样本相互独立,即从一总体中抽取一个样本对从另一总体中抽取一个样本没有任何影响,两个样本的样本量可以不等 

两独立样本t检验的基本步骤

1.提出原假设

对于双侧检验： 

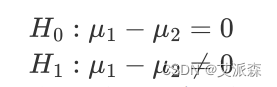
 对于单侧检验，也有相应的原假设和备择假设，μ1，μ2分别为第一个和第二个总体的均值

2.选择检验统计量

        利用两组样本均值的差去估计两总体均值的差。当两总体分布为N(μ1 ,σ1 2)和N(μ2 ,σ2 2)时，两样本均值差的抽样分布仍为正态分布，该正态分布的均值为μ1 -μ2 ,方差为σ12 2。于是，两总体均值差检验的检验统计量为t统计量，数学定义为： 

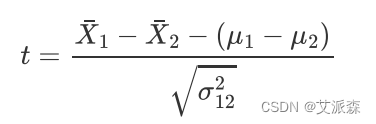
 其中，在不同的情况下σ12 2有不同的计算方式

第一种情况：当两总体方差未知且相等，即σ1=σ2时，

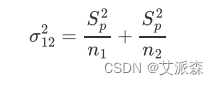
其中：

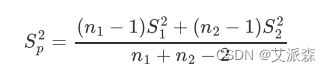
 此时，t统计量服从n1+n2 -2个自由度的t分布；

第二种情况：当两总体方差未知且不相等，即σ1≠σ2时，

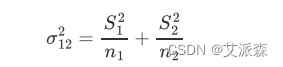
 此时，t统计量服从修正自由度的t分布（这种情况的自由度计算很复杂，无需记忆）

注意：

        两总体方差是否相等是决定t统计量计算的关键。SPSS 中通过Levene F方法推断两总体方差是否有显著差异（原假设是两总体方差无显著差异）。

3.计算检验统计量的观测值和概率P值

4.给定显著性水平α，并作出决策

两独立样本t检验的应用 

注意：

        在进行两独立样本t检验时，SPSS要求将两个样本数据存放在一个SPSS变量中，同时，为区分哪个样本来自哪个总体，还应定义一个存放总体标识的标识变量。 

 【案例】 利用大学生职业生涯规划数据，研究男生与女生的专业和职业认知得分的总体平均值是否存在显著差异。

根据题意，可认为原假设是男女生认知得分的总体均值无显著差异，备择假设为有显著差异，即：

H0 : μ1 -μ2=0

H1 : μ1 -μ2≠0

 操作步骤：

①选择菜单【分析】----> 【比较均值】----> 【独立样本T检验】

②选择检验变量和分组变量

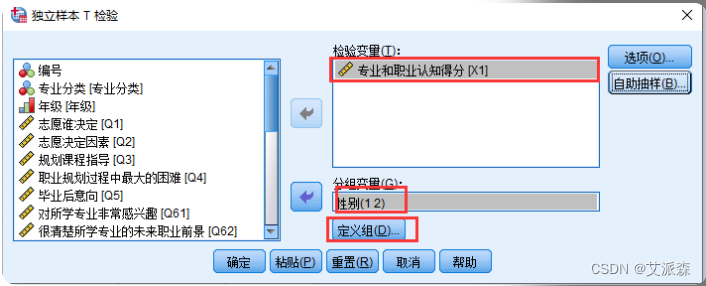
③分析结果如下： 

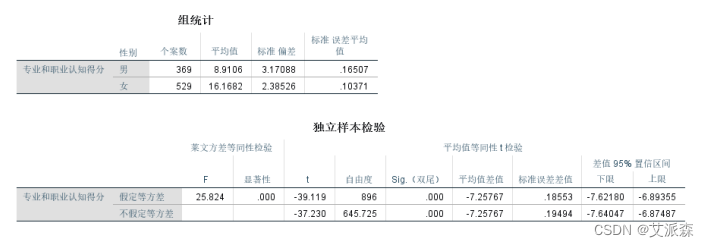
结论：

        从第一个表中可以看出，男生与女生的认知得分的样本平均值有一定差距，这种差距是由抽样误差造成的还是系统性的， 还需要进一步检验。

        第二个表完成的是两独立样本t检验的结果，第一步，两总体方差是否相等的F检验，该检验的F统计量观测值对应的概率P值为 0.000，小于显著性水平α，可以认为两总体的方差有显著差异。第二步，两总体均值差的检验，由于已经认为两总体的方差有显著差异，因此应看第二行（不假定等方差）t检验的结果。其中，t统计量的观测值为-37.230，对应的双侧概率P值为0.000，小于显著性水平α，可以认为两总体的均值有显著差异，即男女生认知得分的总体均值存在显著差异。