KMP算法是一个字符串匹配算法,总的意义是在给定的字符串A中利用优化的方法快速地找出字符串B的位置,相比于传统匹配算法,它能有效减少匹配时间,提高效率。
前缀和后缀
在我们看KMP算法前我们先考虑一个问题:假如我们想要在字符串s里面检索其是否包含了某个字串p。例如字符串s是“abcdabcdf”,字符串p为“dab”,那么按照我们之前的理解,可以从字符串s第一个字符开始,和字符串p中每一个字符进行逐项对比。如果有出入,需要从字符串s的下一个元素开始又重新与字符串p中的每个元素逐项对比。
#include<iostream>
using namespace std;
const int N = 10, M = 4;
int main()
{
char s[N] = "abcdabcdf";
char p[M] = "dab";
for (int i = 0; i < N-1; i++)
{
int flag = 1;
int tmp = i;
for (int j = 0; j < M-1; j++)
{
if (s[tmp++] != p[j])
{
flag = 0;
break;
}
}
if (flag == 1)
{
cout <<"下标为:" << i << endl;
break;
}
}
return 0;
}
而正是因为上面这种排序方式很耗费时间,所以KMP字符串算法诞生了。KMP算法是一种典型的以空间换时间的字符串匹配算法。在了解KMP之前,我们需要知道两个概念:一个字符串的相等前缀和后缀。举个例子:有一个字符串”dabbcda“,前缀是一个字符串字串,它是指从第一个元素开始到后面(除结尾外)的任意一个元素截止中间的字符串。例如前面字符串的前缀就有(d、da、dab、dabb、dabbc、dabbcd);类似地,它的后缀是指以最后一个元素为截止,向前(除开头元素)的任意元素为起始的中间字符串。前面字符串的后缀就有(a、da、cda、bcda、bbcda、abbcda)。而相等前缀\后缀就是前缀和后缀共有的字符串,前面的字符串的相等前缀\后缀就是字符串字串da。
KMP算法匹配原理
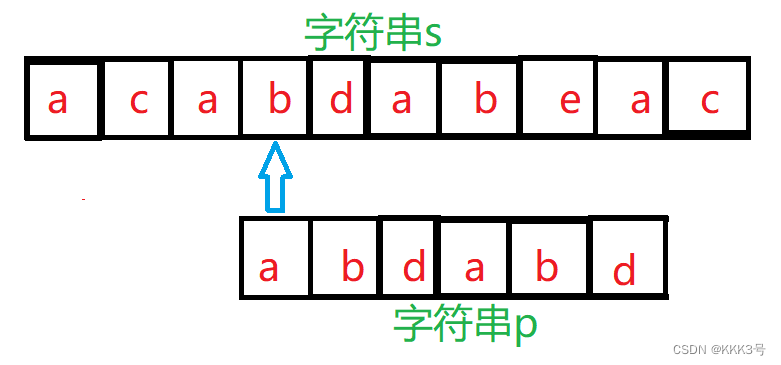
现在我们看看在一次匹配过程中利用KMP算法的匹配过程:例如我们有一个字符串s(acabdabeac)和p(abdabd),我们需要在s里面找出是否有p,若有则返回该字串p在字符串s完全匹配后的首元素下标。
一开始还是照常用p中的每一个字符和s字符串中的每一个字符进行对比,比不上则p继续向s字符串的下一个字符的字串进行对比,注意在匹配到两个及以上的元素时KMP的优势就可以显现出来了。
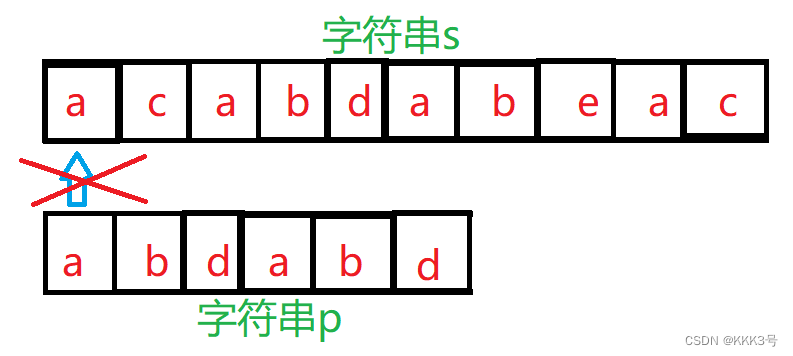

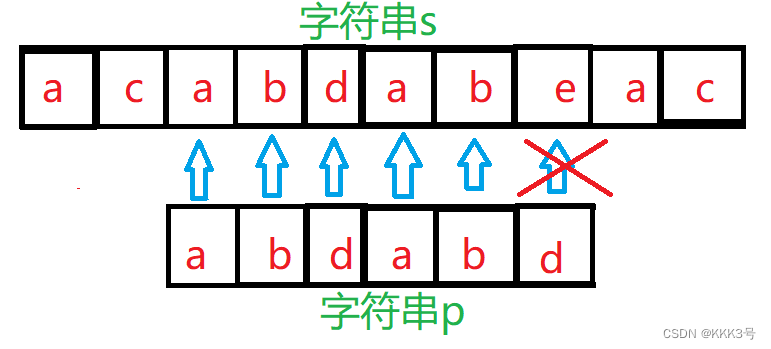
直至上面我们执行到第三遍时,字符串p中的前面5个元素都和字符串s中间的几个元素对上了,但是到了最后一个元素却对不上了,这时候KMP的处理方式就不同与之前我们传统的处理方式。传统的处理方式是下一次重新将字符串p中的a和字符串s中的b进行对比:
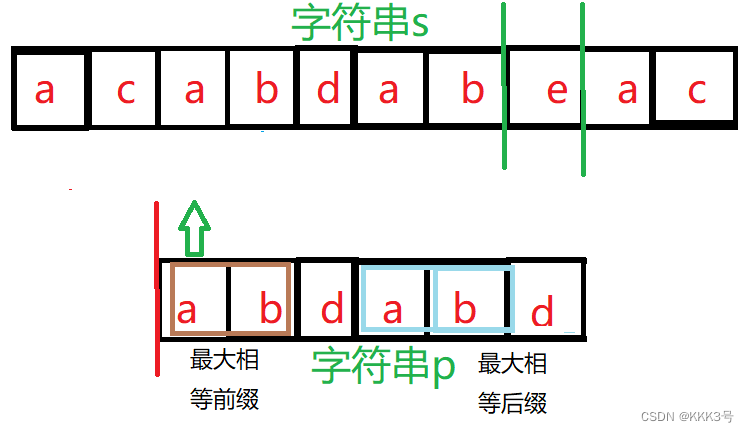
而KMP算法的处理方式不同,当s字符串仅匹配到局部的p字符串,以p字符串中第一个与s字符串相异的元素左边的元素集合为子串,这个子串的最大相等前缀的首元素与之前和其最大相等后缀第一个元素比较的那个s字符串中的元素再对齐(即子串p的前缀镦到其后缀的位置)。以下面的例子为例:第三次匹配时p字符串前面5个字符都匹配上了,唯独后面的d匹配不上,这时候利用KMP算法,字符串p以d为分界,左边字串最大相等前缀/后缀为ab,所以字符串p的前缀将会镦到其后缀的地方。

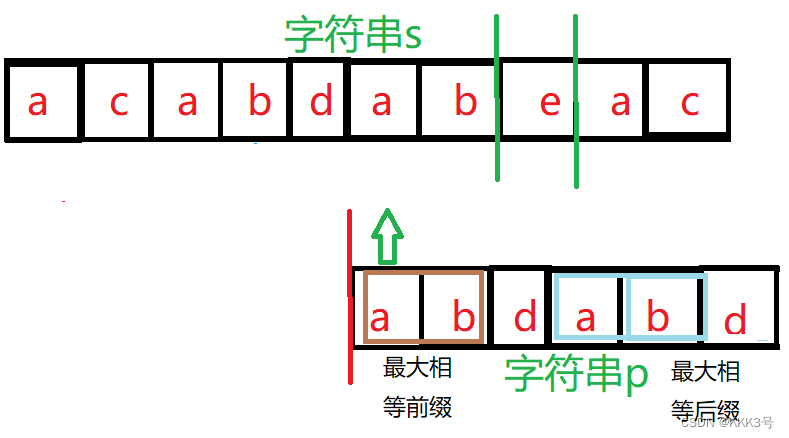
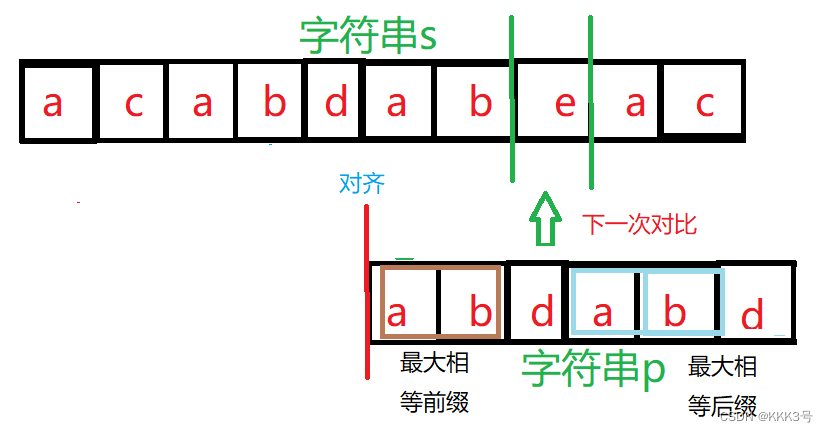
并且将会从其前缀后的第一个元素m开始和字符串s对应的元素开始逐项对比,而不是回溯到字符串p的第一个元素。而这个元素m的位置可以由next数组确定。next数组存储着p字符串中每个元素所对应子串的最大相等前缀/后缀的长度,而这个开始对比的元素的位置就是p[next[2](next数组存储的第三个元素,d元素对应的最大前缀/后缀长度)]
next数组
next数组是KMP算法中存储模式串(上文中字符串p)中以某一个元素为结束的子串的最大相等前缀/后缀的长度。举个例子:字符串abcdabef。以a为结束的子串为a,它的最大相等前缀/后缀为0,相似地,可以算出以b为结束的子串最大相等前缀/后缀为0.....,而next数组里面对应每一个位存储的就是模式串中以对应位为结束的字串的最大相等前缀/后缀的长度。它们的关系如下表所示:
| 结束的元素 | 子串 | 最大相等前缀/后缀长度 | next数组的存储 |
| a | a | 0 | next[0]=0 |
| b | ab | 0 | next[1]=0 |
| c | abc | 0 | next[2]=0 |
| d | abcd | 0 | next[3]=0 |
| a | abcda | 1 | next[4]=1 |
| b | abcdab | 2 | next[5]=2 |
| e | abcdabe | 0 | next[6]=0 |
| f | abcdabef | 0 | next[7]=0 |
知道了next数组的作用,我们再来看看如何用代码将next数组实现:首先我们来看看总代码:
const int Smax = 100, Pmax = 10;
char s[Smax],p[Pmax];
int s_len, p_len;
int ne[Pmax];
for (int i = 1, j = 0; i < p_len; i++)
{
while (j && p[i] != p[j])
j = ne[j];
if (p[i] == p[j])
j++;
ne[i] = j;
}这里的 i 表示字符串p的元素下标,我们需要逐个求出字符串p每一项元素对应子串的最大相等前缀/后缀的长度。这里我们使用到的是一个for循环来对字符串p的每个元素进行计算,我们从下标1开始,因为任何一个字符串的第一个元素的最大相等前缀/后缀的长度肯定是0。j是最大相等前缀/后缀的长度。为了理解for循环里面的内容,我们假设一个场景:目前字符串p匹配到下标为 i 的元素,那么要去求的目前这个元素的最大前缀/后缀就需要在之前已经求得的j的基础上匹配p[i]和p[j]的元素。如果相同,那么最大前缀/后缀就加一即对应j++。
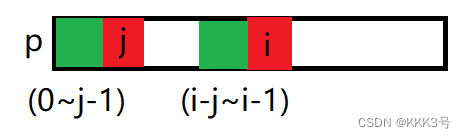
如果不匹配,那么进入while循环,这个循环的意义在于在之前已经找到的最大前缀/后缀的基础上寻找一个更小的最大前缀/后缀(逐渐缩小最大前缀/后缀的过程),下图蓝色部分。
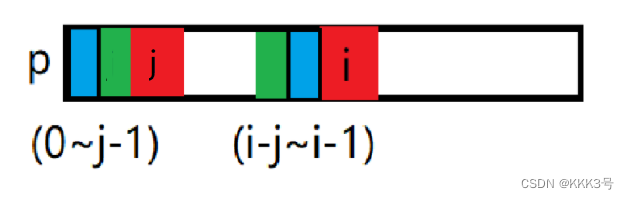
了解了next数组后,我们可以发现实现KMP算法的流程和实现next数组类似,只不过是之前是模式串中的前缀最后一个元素和后缀最后一个元素的对比,这里是s字符串中元素和p字符串中元素的对比。当我们j对比到最后一个元素时,对比上了,那么j会加加变成p的长度,那就代表成功了。这时候就输出当前 i 的位置。记住 i 的头位置是在减去p的长度后加一的位置。
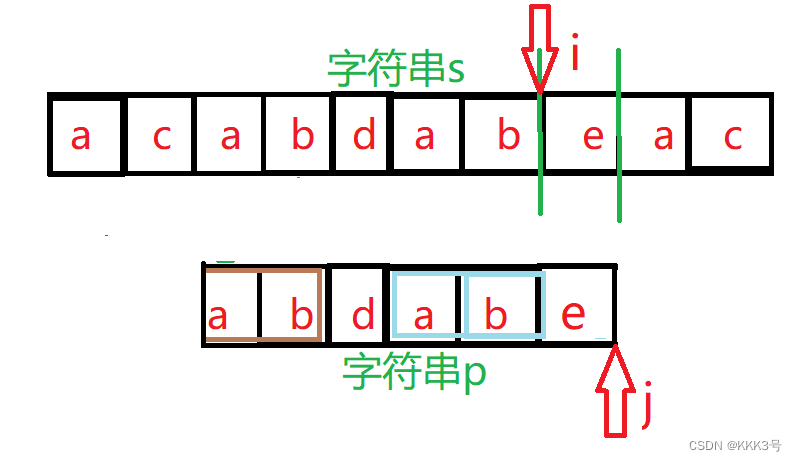
所以匹配代码是:
//kmp匹配过程
for (int i = 0, j = 0; i < s_len; i++)
{
while (j && s[i] != p[j])
j = ne[j];
if (s[i] == p[j])
j++;
if (j == p_len)
{
cout << i - p_len+1<<" ";
j = ne[j];
}总代码
#include<iostream>
using namespace std;
const int Smax = 100, Pmax = 10;
char s[Smax],p[Pmax];
int s_len, p_len;
int ne[Pmax];
int main()
{
cin >> s_len >> s >> p_len >> p ;
//next数组求法
for (int i = 1, j = 0; i < p_len; i++)
{
while (j && p[i] != p[j])
j = ne[j];
if (p[i] == p[j])
j++;
ne[i] = j;
}
//kmp匹配过程
for (int i = 0, j = 0; i < s_len; i++)
{
while (j && s[i] != p[j])
j = ne[j];
if (s[i] == p[j])
j++;
if (j == p_len)
{
cout << i - p_len + 1 <<" ";
j = ne[j];
}
}
return 0;
}上面是我学习KMP算法的笔记,因为我对KMP算法理解可能还不够深入,所以可能对某些地方的叙述有些问题或者哪里有错误,希望大家能够批评指正。
参考资料:
参考资料1
参考资料2
参考资料3
参考资料4