一、改变数组元素（差分）

方法一：差分数组

map(int,input().split())

这个返回的是一个对象，而不是一个整数

for b in arr[:n]:

arr[:n] 是 Python 中的一个切片操作，表示从列表 arr 的开头（索引0）到第 n-1 个元素的子列表。

print(1 if b else 0,end=’ ')

这段代码的作用是将布尔值 b 转换成整数并打印出来。如果 b 为 True，则打印 1，否则打印 0。代码中的 end=’ ’ 表示在打印结果后不换行，而是以空格结尾。

#只用关心某个数字位置是否被覆盖过，不关心覆盖过几次
for i in range(int(input())):#读入输入数组的次数
    n,a=int(input()),list(map(int,input().split()))#前面是传入一个数，后面传的一个数组
    arr=[0]*(n+5)#数组的大小
    for j in range(n):
        arr[max(0,j-a[j]+1)]+=1
        arr[j+1]-=1
    for j in range(1,n):
        arr[j]+=arr[j-1]#差分数组
    for b in arr[:n]:
        print(1 if b else 0,end=' ')#这个用法好绝，对于初学者来说
    print()#换行

方法二：区间合并

这段代码是一个处理区间问题的算法，主要实现以下步骤：

1.读入一个整数 n 和长度为 n 的整数列表 a。

2.对于列表 a 中的每个元素 a[j]，如果它不为零，则将区间 [max(0, j-a[j]+1), j] 添加到 interval 列表中。

3.对 interval 列表按照区间的左端点进行排序。

4.对于排好序的 interval 列表中的每个区间，将该区间内的所有元素在 arr 列表中标记为 1。

5.输出标记好的 arr 列表。

可以看到，该算法的时间复杂度为 O(nlogn)，其中最耗时的操作是对区间列表进行排序。

interval.sort(key=lambda x:x[0])

这段代码是按照左端点进行排序，如果要按照右端点进行排序

interval.sort(key=lambda x: x[1])

for i in range(int(input())):#input()返回为str，转换为int
    n,a=int(input()),list(map(int,input().split()))#输入数组大小及数组元素
    arr,interval=[0]*n,[]
    for j in range(n):
        if a[j]:
            interval.append([max(0,j-a[j]+1),j])#记录区间
    interval.sort(key=lambda x:x[0])#按照区间端点进行排序
    if interval:#检查interval是否为空，若为空则直接输出长度为n的全0数组，
        # 如果不为空，则按照一定的规则将1填充到arr数组中
        p=1#编号为0的区间
        for j in range(1,len(interval)):
            if interval[j][0]>interval[p-1][1]+1:#如果区间左端点大于编号为p-1的一个区间右端点+1，则说明这是两个区间
                interval[p]=interval[j]
                p+=1
            else:#如果在内部，则可以这两个区间
                interval[p-1][1]=max(interval[p-1][1],interval[j][1])
        for j in range(p):#枚举每个区间，将每个区间内所包含的置1
            for k in range(interval[j][0],interval[j][1]+1):
                arr[k]=1
    for a in arr:
        print(a,end=' ')
    print()

注意缩进！！！

二、差分

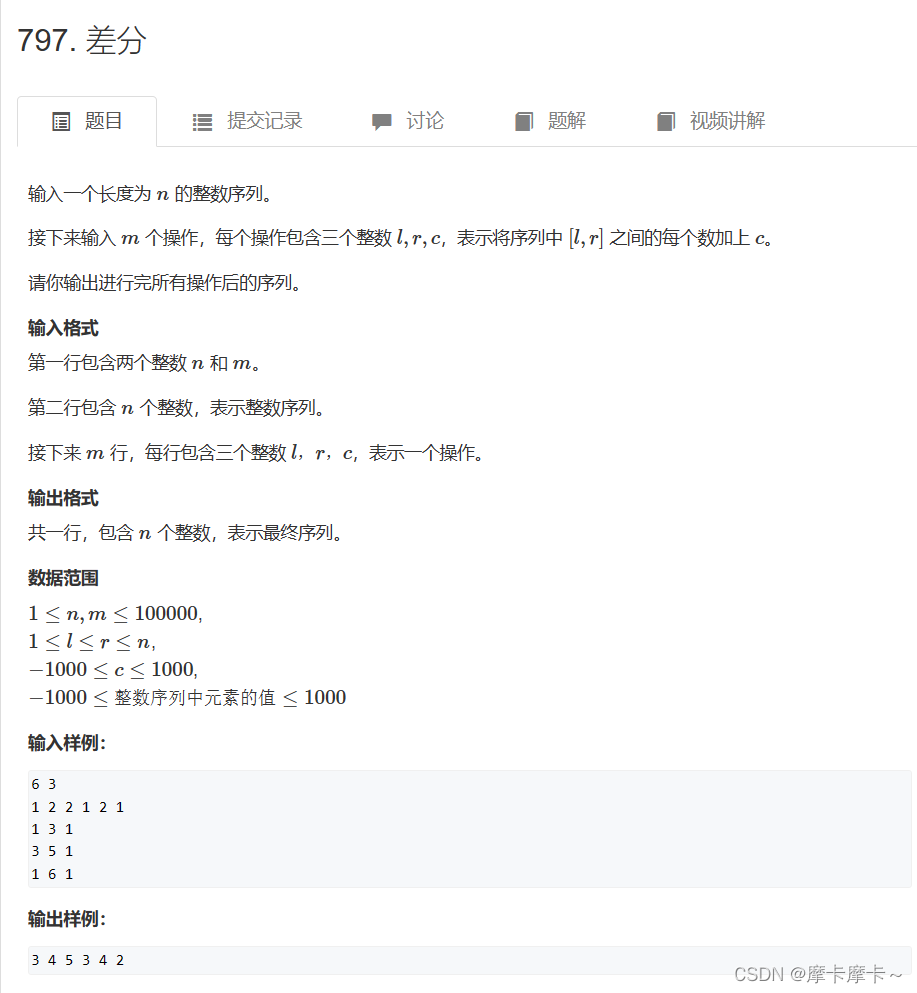
a = [0] + list(map(int, input().split())) + a[n + 1:]

这行代码的作用是将列表a中从下标1到n（包括1和n）的元素替换为输入的元素，并在列表的开头和结尾添加了一个0，保证了后面的操作不会出现索引错误。具体地：

a[:n+1]表示从下标0到n的元素，其中a[0]为列表的第一个元素，a[n]为列表的最后一个元素，a[n+1:]表示从下标n+1到列表结尾的所有元素。

因此，a = [0] + list(map(int, input().split())) + a[n +1:]的作用就是先将0添加到列表的开头，然后将输入的元素添加到原来的位置上，最后再将原来的n+1到结尾的所有元素添加到列表的尾部，从而得到了一个长度为n+2的新列表a。

n,q=map(int,input().split())
a=[0]*(n+10)
b=[0]*(n+10)

#a的0位是0，第1位到第n位是输入的数，第n+1位起往后都是0
a=[0]+list(map(int,input().split()))+a[n+1:]
for i in range(1,n+1):
    b[i]=a[i]-a[i-1]#初始化b数组
    
while q:
    l,r,c=map(int,input().split())
    b[l]+=c
    b[r+1]-=c
    q-=1
    
#a数组没有用了，将a更新一遍
for i in range(1,n+1):
    a[i]=a[i-1]+b[i]
    print(a[i],end=' ')

三、差分矩阵

写法一：

def insert(matrix,x1,y1,x2,y2,c):#差分数组
    matrix[x1][y1]+=c
    matrix[x2+1][y1]-=c
    matrix[x1][y2+1]-=c
    matrix[x2+1][y2+1]+=c

def main():
    n, m, q = map(int, input().split())
    matrix=[[0 for i in range(m+10)] for j in range(n+10)]#定义二维数组
    for i in range(1,n+1):
        row =list(map(int, input().split()))
        for j in range(m):
            insert(matrix,i,j+1,i,j+1,row[j])
            
    for i in range(q):
        x1,y1,x2,y2,c=map(int,input.split())
        insert(matrix,x1,y1,x2,y2,c)
        
    for i in range(1,n+1):
        for j in range(1,m+1):
            matrix[i][j]+=matrix[i-1][j]+matrix[i][j-1]-matrix[i-1][j-1]
            print(matrix[i][j],end=" ")
        print()

if __name__=="__main__":
    main()

写法二：

print(" ".join(map(str,dt[i][1:m+1])))

这行代码将列表dt[i][1:m+1]中的元素转换成字符串，然后用空格连接起来，并打印输出。其中：

1. map(str, dt[i][1:m+1]) 表示将列表 dt[i][1:m+1] 中的每个元素都转换成字符串类型；
2. " ".join(…) 表示将字符串列表中的元素用空格连接起来，形成一个新的字符串；
3. print(…) 表示将拼接好的字符串打印输出。

def insert(b,x1,y1,x2,y2,c):
    b[x1][y1] += c
    b[x2+1][y1] -= c
    b[x1][y2+1] -= c
    b[x2+1][y2+1] += c

n,m,q = map(int,input().split())
ls = []
dt = [[0 for _ in range(1010)] for _ in range(1010)]
for i in range(n):
    ls.append(list(map(int,input().split())))
for i in range(1,n+1):
    for j in range(1,m+1):
        insert(dt,i,j,i,j,ls[i-1][j-1])
while q >0:
    q -= 1
    x1,y1,x2,y2,c = map(int,input().split())
    insert(dt,x1,y1,x2,y2,c)
for i in range(1,n+1):
    for j in range(1,m+1):
        dt[i][j] +=dt[i-1][j]+dt[i][j-1] - dt[i-1][j-1]
for i in range(1,n+1):
    print(" ".join(map(str,dt[i][1:m+1])))

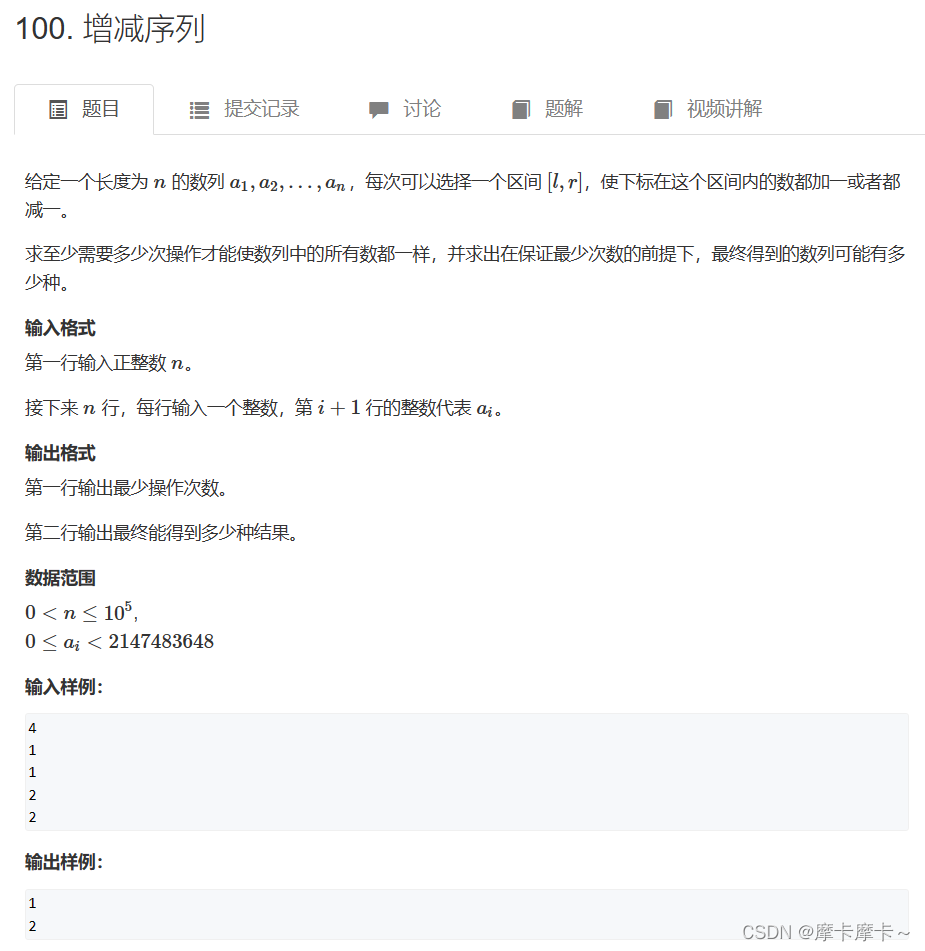
四、增减序列

差分解决一段区域同时增加或减少的问题
给区间【L，R】上都加上一个常数c，则b[L] += c , b[R + 1] -=c

求出a的差分序列b，其中b1 = a1,b(i) = a(i) - a(i - 1) (2 <= i <= n)。令b(n + 1) = 0，题目对序列a的操作，相当于每次可以选出b1,b2…b(n + 1)中的任意两个数，一个加1，另外一个减一。目标是把b2,b3,…bn变为全0。最终得到的数列a就是由 n 个 b1 构成的

任选两个数的方法可分为四类
1、2 <= i , j <=n（优先）
2、i = 1, 2 <=j <=n
3、2 <= i <= n , j = n + 1
4、i = 1, j = n + 1（没有意义）

设b2,b3…bn中正数总和为p，负数总和的绝对值为q。首先以正负数匹配的方式尽量执行1类操作，可执行min(p,q)次。剩余|p - q|个为匹对，每个可以选与b1或b(n + 1)匹配，即执行2 或 3 类操作，共需|p - q|次

综上所诉，最少操作次数为min(p,q) + |p - q|。根据|p - q|次第2、3类操作的选择情况，能产生|p - q| + 1中不同的b1的值，即最终得到的序列a可能有|p - q| + 1 种

print(f"{max(pos, neg)}\n{abs(pos - neg) + 1}")

这是一种 f-string 的写法，用于格式化字符串。其中，大括号内的部分会被替换为相应的变量或表达式的值。具体来说：

f"xxx"：表示这是一个 f-string，其中 xxx 是字符串内容，可以包含普通文本和大括号表达式。
{max(pos, neg)}：表示一个大括号表达式，会被替换为 pos 和 neg 中的最大值。
\n：表示换行符。
{abs(pos - neg) + 1}：表示一个大括号表达式，会被替换为 pos 和 neg 的差值的绝对值加上 1。

n = int(input())
a = [0] * (n + 2)
for i in range(1,n+1):
    x = int(input())
    a[i] += x
    a[i+1] -= x

pos, neg = 0, 0
for i in range(2, n+1):
    if a[i] > 0:
        pos += a[i]
    else:
        neg -= a[i]

print(f"{max(pos, neg)}\n{abs(pos - neg) + 1}")