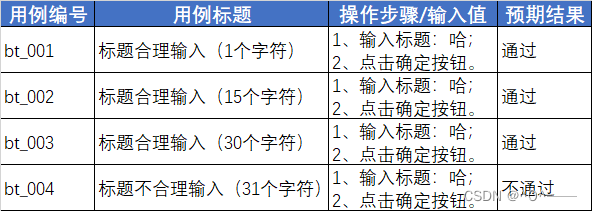
知识要点

TensorFlow是深度学习领域使用最为广泛的一个Google的开源软件库 .
TensorFlow中定义的数据叫做Tensor(张量), Tensor又分为常量和变量.
- 常量一旦定义值不能改变.
定义常量: t = tf.constant([[1., 2., 3.], [4., 5., 6.]])
定义变量: v = tf.Variable([[1., 2., 3.], [4., 5., 6.]])
tensor 转换为numpy 数组: print(t.numpy())
常量里面是字符串时: d = tf.constant('abcd')
创建不整齐的tensor: r = tf.ragged.constant([[11, 12], [21, 22, 23], [], [41]])
拼接张量: print(tf.concat([r, r2], axis = 0))
s = tf.SparseTensor(indices=[[0, 1], [1, 0], [2, 3]], values = [1, 2, 3], dense_shape = [3, 4]) # 生成稀疏矩阵
转换为稠密矩阵: print(tf.sparse.to_dense(s))
定义变量: v = tf.Variable([[1, 2, 4], [3, 5, 6]])
对变量的某个位置进行赋值: v[0, 1].assign(42)
可以指定聚合的轴上的平均值: x_reduce_mean = tf.reduce_mean(x, axis=0)
按列求和: print(x.sum(axis = 0)) # [16 15 20 21 16 22]
矩阵运算: dot = tf.matmul(x, y)

1 TensorFlow简介

1.1 TensorFlow基础

TensorFlow是深度学习领域使用最为广泛的一个Google的开源软件库（最初由Google brain team进行开发的内部库，由于它的易用性Google决定把它开源出来）.
采取数据流图，用于数值计算.
- 节点 —— 处理数据
- 线 —— 节点间的输入输出关系
- 数据流图中的数据叫做tensor, 表示张量, 即N维数据, tensor在数据流图中流动表示计算的过程, 这也是tensorflow名字的由来.

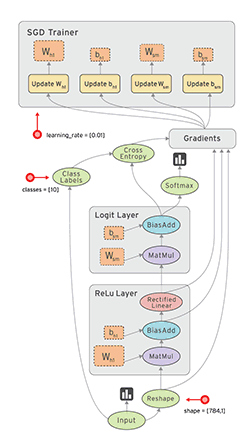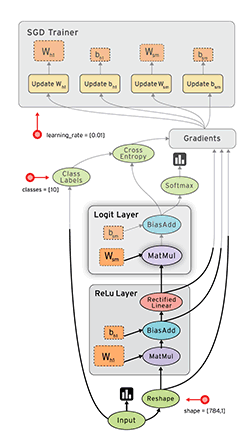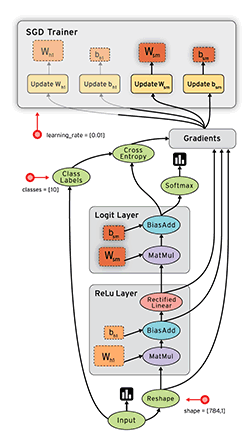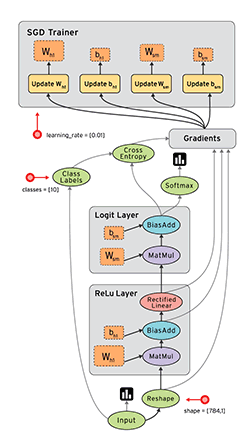
支持多种平台，GPU、CPU、移动设备
tensorflow特性:
- 高度的灵活性: 只要能把数据的计算表示成数据流图就可以使用tensorflow
- 真正的可移植性: 比如CPU、GPU、移动设备等等
- 产品和科研结合
  - tensorflow研究最初是用于科研的，其实科研和工程还有一定的距离，科研的代码需要进一步各种各样的优化才能真正的做到产品上去，但是对于tensorflow则没有这个问题，Google团队把tensorflow优化的已经比较好了，做研究的代码可以无缝的用到产品上
- 自动求微分
- 多语言支持
  - tensorflow除了python以外，还支持各种各样的语言，比如说c++、java、javascript、R语言等
- 性能最优化
  - 在tensorflow刚刚出来的时候由于它运行的比较慢，很多深度学习库呢都会拿tensorflow来进行比较，然后来证明自己比tensorflow好多少倍，但是随着tensorflow一步一步的进行开发，这种情况一去不复返了，tensorflow现在应该是运行最快的一个库，对于分布式的tensorflow来说，它的加速比几乎是线性的

1.2 tensorflow 2.0 架构特点

tensorflow2.0 主要特性:

使用 tf.keras 和 eager mode（动态图模式）进行更简单的模型构建.
- 使用tf.data加载数据
- 使用tf.keras构建模型，也可使用premade, estimator来验证模型
  - 使用tensorflow hub进行迁移学习
- 使用eager mode运行和调试
- 使用分发策略来进行分布式训练
- 导出到SavedMode
- 使用TensorFlow Serve、Tensorflow Lite、Tensorflow.js部署模型
鲁棒的跨平台模型部署
- TensorFlow服务
  - 直接通过HTTP/RESR或GRPC/协议缓冲区
- TensorFlow Lite——可部署到Android、iOS和嵌入式系统上
- TensorFlow.js——在JavaScript中部署
- 其他语言
  - C、Java、Go、C#、Rust、Julia、R等
强大的研究试验
- Keras功能API和子类API、允许创建复杂的拓扑结构
- 自定义训练逻辑、使用tf.GraddientTape和tf.custom_gradient进行更细粒度的控制
- 底层API自始至终可以与高层结合使用、完全的可定制
- 高级扩展：Ragged Tensor、Tensor2Tensor等
清除不推荐使用的API和减少重复来简化API

2 基础API使用

TensorFlow中定义的数据叫做Tensor(张量), Tensor又分为常量和变量.

2.1 常量的定义和使用

常量一旦定义值不能改变. 使用tf.constant定义常量.

使用tf.constant定义常量

# 常量一旦定义, 不能变, 不可更改
import tensorflow as tf
t = tf.constant([[1., 2., 3.], [4., 5., 6.]])
# 可以像numpy的ndarray一样使用tensor
print(t)     # tf.Tensor([[1. 2. 3.], [4. 5. 6.]], shape=(2, 3), dtype=float32)
print(t[:, 1:])    # tf.Tensor([[2. 3.], [5. 6.]], shape=(2, 2), dtype=float32)
print(t[..., 1])   # 或t[:, 1]  # tf.Tensor([2. 5.], shape=(2,), dtype=float32)

常量的操作

print(t+10)   # 每个元素都加10
print(tf.square(t))   # 每个元素都做平方
print(t @ tf.transpose(t))   # @表示矩阵的点乘

常量tensor和numpy中的ndarray的转化
- tf.constant(numpy) # 将numpy数组转换为tensor

import numpy as np
# .numpy()可以把tensor转化为ndarray
print(t.numpy())    # 转换为numpy数组  [[1. 2. 3.], [4. 5. 6.]]
print(np.square(t))    # 直接转换  [[ 1.  4.  9.], [16. 25. 36.]]
np_t = np.array([[1., 2., 3.], [4., 5., 6.]])
# 直接使用ndarray生成一个tensor
print(tf.constant(np_t))    # tf.Tensor([[1. 2. 3.], [4. 5. 6.]], shape=(2, 3))

生成标量

# scalar
t = tf.constant(2.718)
print(t.numpy())    # 2.718
print(t.shape)     # ()

切片

a[:, 1:].numpy()   # array([[2, 3], [5, 6]])

... 表示逗号前所有的维度

# 特有的写法
# ... 表示逗号前所有的维度, 只取最后一个维度的值(二维时,取其中列的值)
a[..., 1:]
'''<tf.Tensor: shape=(2, 2), dtype=int32, numpy=array([[2, 3], [5, 6]])>'''

使用字符串

t = tf.constant("cafe")  # # strings
print(t)  # tf.Tensor(b'cafe', shape=(), dtype=string)
print(tf.strings.length(t)) # 获取字符串的长度  tf.Tensor(4, shape=(), dtype=int32)
print(tf.strings.length(t, unit="UTF8_CHAR")) # 获取utf8编码的长度
print(tf.strings.unicode_decode(t, "UTF8")) # 把字符串转化为utf8编码

常量里面是字符串

# 常量里面是字符串时
d = tf.constant('abcd')
d   # <tf.Tensor: shape=(), dtype=string, numpy=b'abcd'>

使用字符串数组
- 字符串的一些方法: tf.strings.length(d)
- utf8的编码长度: tf.strings.length(d, unit = 'UTF8_CHAR')
- 字符编码方式的转化: tf.strings.unicode_decode(d, 'UTF8')

# string array
t = tf.constant(["cafe", "咖啡"])
print(tf.strings.length(t, unit="UTF8_CHAR"))  # tf.Tensor([4 2], shape=(2,))
r = tf.strings.unicode_decode(t, "UTF8")
print(r)    # <tf.RaggedTensor [[99, 97, 102, 101], [21654, 21857]]>

创建ragged tensor # ragged tensor 不整齐的tensor, 上面的tensor每个字符串长度不一致.

r = tf.ragged.constant([[11, 12], [21, 22, 23], [], [41]])
# index op
print(r)   # <tf.RaggedTensor [[11, 12], [21, 22, 23], [], [41]]>
print(r[1])  # tf.Tensor([21 22 23], shape=(3,), dtype=int32)
# 左闭右开
print(r[1:2])   # <tf.RaggedTensor [[21, 22, 23]]>

ragged tensor的操作: 拼接张量的函数

r2 = tf.ragged.constant([[51, 52], [], [71]])
# 拼接操作, axis=0按行拼接. 如果按列拼接会报错. 因为行数不一致.
print(tf.concat([r, r2], axis = 0))
'''<tf.RaggedTensor [[11, 12], [21, 22, 23], [], [41], [51, 52], [], [71]]>'''

按列拼接

r3 = tf.ragged.constant([[13, 14], [15], [], [42, 43]])
print(tf.concat([r, r3], axis = 1))
'''<tf.RaggedTensor [[11, 12, 13, 14], [21, 22, 23, 15], [], [41, 42, 43]]>'''

把 ragged tensor 转化为普通tensor

# 缺元素的地方会补0, 0在正常元素的后面.
print(r.to_tensor())
'''tf.Tensor(
[[11 12  0]
 [21 22 23]
 [ 0  0  0]
 [41  0  0]], shape=(4, 3), dtype=int32)'''

创建 sparse tensor # sparse tensor 稀疏 tensor, tensor中大部分元素是0, 少部分元素是非0.

# indices指示正常值的索引, 即哪些索引位置上是正常值. values表示这些正常值是多少.
# indices和values是一一对应的. [0, 1]表示第0行第1列的值是1, [1,0]表示第一行第0列的值是2,
# [2, 3]表示第2行第3列的值是3, 以此类推.
# dense_shape表示这个SparseTensor的shape是多少
s = tf.SparseTensor(indices = [[0, 1], [1, 0], [2, 3]],
                    values = [1., 2., 3.],
                    dense_shape = [3, 4])
print(s)
# 把sparse tensor转化为稠密矩阵 
print(tf.sparse.to_dense(s))

sparse tensor的运算

# 乘法
s2 = s * 2.0
print(s2)
try:
    s3 = s + 1   # 加法不支持.
except TypeError as ex:
    print(ex)
s4 = tf.constant([[10., 20.],
                  [30., 40.],
                  [50., 60.],
                  [70., 80.]])
# 得到一个3 * 2 的矩阵
print(tf.sparse.sparse_dense_matmul(s, s4))

注意在定义sparse tensor的时候 indices 必须是排好序的. 如果不是, 定义的时候不会报错, 但是在to_dense的时候会报错

# [0, 2]在[0, 1]前面
s5 = tf.SparseTensor(indices = [[0, 2], [0, 1], [2, 3]],
                    values = [1., 2., 3.],
                    dense_shape = [3, 4])
print(s5)
# 可以通过reorder对排序, 这样to_dense就没问题了.
s6 = tf.sparse.reorder(s5)
print(tf.sparse.to_dense(s6))

2.2 变量的使用

变量和常量相对, 变量定义之后可以改变值.

通过tf.Variable来定义变量

# 变量, 即内部的值可以变化, 比如神经网络中的w, b 就是变量
# tf.Variable 来定义即可
v = tf.Variable([[1, 2, 4], [3, 5, 6]])
print(v)
'''<tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy=
array([[1, 2, 4],
       [3, 5, 6]])>'''

对变量进行赋值 # 注意: 变量赋值必须使用assign, 不能直接用=.

# 对变量之间赋值, 所有位置乘于2
v.assign(2*v)
print(v.numpy())     # [[ 2  4  8] [ 6 10 12]]
# 对变量的某个位置进行赋值
v[0, 1].assign(42)
print(v.numpy())     # [[ 2 42  8] [ 6 10 12]]
# 对变量的某一行赋值
v[1].assign([7, 8, 9])
print(v)   # array([[ 2, 42,  8], [ 7,  8,  9]])>

2.3 TensorFlow的数学运算

在TensorFlow中既可以使用数学运算符号进行数学运算也可以使用TensorFlow定义的方法.

# 两种方式, 一种是直接用python的算术运算符, 另一种使用TensorFlow封装的数学运算函数
# 定义常量
a = tf.constant(2)
b = tf.constant(3)
c = tf.constant(5)

# 定义运算, 也可以直接使用python运算符+,-, * / ...
add = tf.add(a, b)
sub = tf.subtract(a, b)
mul = tf.multiply(a, b)
div = tf.divide(a, b)

# 打印运算结果
print("add =", add.numpy())    # add = 5
print("sub =", sub.numpy())    # sub = -1
print("mul =", mul.numpy())    # mul = 6
print("div =", div.numpy())    # div = 0.6666666666666666
print('数学+运算 a+b=', (a + b).numpy())  # 数学+运算 a+b= 5

聚合运算
- 用于计算张量tensor沿着指定的数轴上的的平均值: tf.reduce_mean(x)

x = np.random.randint(0,10, size=(3,6))
print(x)  
'''[[2 1 8 7 7 8]
    [6 7 6 6 1 8]
    [8 7 6 8 8 6]]'''
x_mean = tf.reduce_mean(x)
# 默认会聚合所有的维度
print(x_mean.numpy())    # 6
# 按列求和
print(x.sum(axis = 0))   # [16 15 20 21 16 22]
# 可以指定聚合的轴
x_reduce_mean = tf.reduce_mean(x, axis=0)
print(x_reduce_mean.numpy())   # [5 5 6 7 5 7]

矩阵运算

# 矩阵运算
x = np.random.randint(0,10, size=(3,6))
y = np.random.randint(0,10, size=(6,4))
dot = tf.matmul(x, y)
# 矩阵乘法的简写: x @ y
print(dot.numpy())
''' [[ 59  85  65  96]
     [143 125 116 211]
     [ 83  83  89 116]]'''