前言

月末了，划个水，赶一下指标（更新一些活跃值，狗头）
本文主要是关于线段树的内容。这个线段树的话，主要是适合求解我们一个数组的一些区间的问题，例如区间之和，区间乘机，区间最大，最小值等（当然求和，求乘机啥的，直接用前缀数组，如果是一些区间的大小的问题的话，当然用这个是比较合适的，当然这依然是空间换取时间的操作。例如一个数组长度为N，那么当我们构建这颗线段树时，我们所需要花费的空间为4N（为了保证不越界).

特点

首先的话，要说的关于线段树的特点其实就几个，第一就是数据存放在叶子节点，非叶子节点表示的是我们想要求取的目标值，例如我们想要求取一个区间和，那么非叶子节点存储的就是这个小区间内的值。

第二个特点就是Lazy懒惰更新，这个有点类似于摊还分析当中提到的第二种方式，每个元素的花费需要考虑到当前的消费和将来的消费，将来的消费，用于将来的花费。这个Lazy其实也有类似的意思，我先标记一下，然后我要用的到的时候，我再进行操作，起到了一个预知未来，延迟操作的意思。同样的，代码实现比较简单，至少比红黑树，斐波那契堆简单。

那么关于这个特点的话，这里先插一个眼，具体的将在下面进行阐述。
本文的话，就从区间求和为案例进行说明，这里面可以覆盖到较多的操作。

操作

数据存储

首先的话，这个数据的存储其实就是下面的样子。

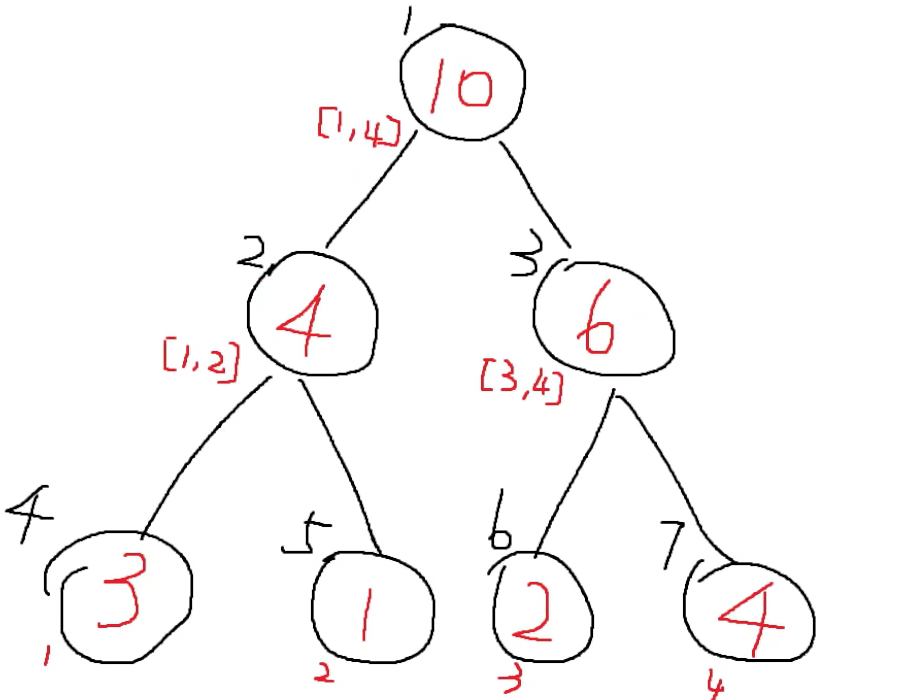
然后这个叶子节点的话就是我们的这个数据，然后的话，这里也是对半砍掉一组数据，然后递归，跟那个归并有点像。

update

然后就是修改，这个的话就开始体现到Lazy的作用了，首先我们知道一个节点，他其实表示了当前这个节点表示的是哪个区间的一个值，用代码表示他的一个数据结构其实就是这样的：

    class __Node():
        l: int = 0
        r: int = 0
        v: int = 0
        lazy: int = 0

        def __str__(self):
            return "left:{},right{},value:{},lazy:{}".format(self.l, self.r, self.v, self.lazy)

所以这个Update的话，明确一个区间，然后呢，我们找到这个区间，然后秉承着lazy的原则，如果我们发现，如果我们要更新的区间能够覆盖我们当前的这个节点的区间，我们就直接更新好这个节点的值，然后这个Lazy，记录一些我们修改的值是啥。

    def update(self, i, l, r, k):
        if (self.tree[i].l >= l and self.tree[i].r <= r):
            self.tree[i].v += k * (self.tree[i].r - self.tree[i].l + 1)
            self.tree[i].lazy = k
            return
        if (self.tree[i].lazy != 0):
            self.__putdown(i)
        if (self.tree[2 * i].r >= l): #和左孩子还有交集
            self.update(2 * i, l, r, k)
        if (self.tree[2 * i + 1].l <= r): #和右孩子还有交集
            self.update(2 * i + 1, l, r, k)
        self.tree[i].v = self.tree[2*i].v+self.tree[2*i+1].v

之后的话，我们跟新一下，当然这里还需要注意的是，就是如果没有完全覆盖的话，我们需要更新一下Lazy，此时给到孩子节点，为什么要更新呢，原因的话就是当前的节点已经不能覆盖了，需要用到孩子节点，但是原来孩子节点没有更新值，现在要用了，就得把孩子赶紧更新一下，然后重新更新当前作为父节点的i。

Lazy下移

这个下移的话就是刚刚提到的，因为这个Lazy就相当于一个标记。他是这样的。

    def __putdown(self, i):

        self.tree[2 * i].lazy += self.tree[i].lazy
        self.tree[2 * i + 1].lazy += self.tree[i].lazy
        mid = (self.tree[i].l + self.tree[i].r) // 2
        self.tree[2 * i].v += self.tree[i].lazy * (mid - self.tree[i].l + 1)
        self.tree[2 * i + 1].v += self.tree[i].lazy * (self.tree[i].r - mid)
        self.tree[i].lazy = 0

更新孩子的Lazy，然后去掉父节点的Lazy，然后更新值。

查询

查询也是一致的，和更新一样，只是少了元素的更新，这里依然需要这个Lazy的下移，而且其实这个Lazy的下移其实就是在重新计算我们的修改，假设一直都没有用到，就一直不会更新，这样就节省了运算。就比如，你买了一张4080ti,但是你一直没有时间happy，那么在你没有happy时间的情况下就提前买了显卡，那么就浪费了这个money，因为早买没有享受到，但是当你有happy time的时候，你再去买，那么就是及时享乐了，没有造成资源的空闲浪费，搞不好还降价了，嘿嘿~

    def search(self, i, l, r):
        if (self.tree[i].l >= l and self.tree[i].r <= r):
            return self.tree[i].v
        if (self.tree[i].lazy != 0):
            self.__putdown(i)
        t = 0
        if (self.tree[2 * i].r >= l):
            t += self.search(2 * i, l, r)
        if (self.tree[2 * i + 1].l <= r):
            t += self.search(2 * i + 1, l, r)
        return t

实现

""" 
为了方便建树，这里的话我们将从1开始作为我们的下标
"""
class SegmentTree(object):
    def __init__(self, date):
        self.date = [0] + date
        self.len_date = len(self.date)
        self.tree = [self.__Node() for _ in range(4 * self.len_date)]
        self.__build(1, 1, self.len_date - 1)

    def __build(self, i, l, r):

        self.tree[i].l = l
        self.tree[i].r = r
        if (l == r):
            self.tree[i].v = self.date[r]
            return
        mid = (l + r) // 2
        self.__build(2*i, l, mid)
        self.__build(2*i+1, mid + 1, r)
        self.tree[i].v = self.tree[i * 2].v + self.tree[i * 2 + 1].v

    def search(self, i, l, r):
        if (self.tree[i].l >= l and self.tree[i].r <= r):
            return self.tree[i].v
        if (self.tree[i].lazy != 0):
            self.__putdown(i)
        t = 0
        if (self.tree[2 * i].r >= l):
            t += self.search(2 * i, l, r)
        if (self.tree[2 * i + 1].l <= r):
            t += self.search(2 * i + 1, l, r)
        return t

    def update(self, i, l, r, k):
        if (self.tree[i].l >= l and self.tree[i].r <= r):
            self.tree[i].v += k * (self.tree[i].r - self.tree[i].l + 1)
            self.tree[i].lazy = k
            return
        if (self.tree[i].lazy != 0):
            self.__putdown(i)
        if (self.tree[2 * i].r >= l):
            self.update(2 * i, l, r, k)
        if (self.tree[2 * i + 1].l <= r):
            self.update(2 * i + 1, l, r, k)
        self.tree[i].v = self.tree[2*i].v+self.tree[2*i+1].v

    def __putdown(self, i):

        self.tree[2 * i].lazy = self.tree[i].lazy
        self.tree[2 * i + 1].lazy = self.tree[i].lazy
        mid = (self.tree[i].l + self.tree[i].r) // 2
        self.tree[2 * i].v += self.tree[i].lazy * (mid - self.tree[i].l + 1)
        self.tree[2 * i + 1].v += self.tree[i].lazy * (self.tree[i].r - mid)
        self.tree[i].lazy = 0


    class __Node():
        l: int = 0
        r: int = 0
        v: int = 0
        lazy: int = 0

        def __str__(self):
            return "left:{},right{},value:{},lazy:{}".format(self.l, self.r, self.v, self.lazy)

这里的话，注意，找的时候呢，是从1号节点开始的，1号节点不等于第一个元素！

if __name__ == '__main__':
    a = [1,2,3,4,5]
    seg = SegmentTree(a)
    seg.update(1,5,5,5) #从根节点开始找，更新区间为[5,5]的元素+5，也就是第五个元素+5
    print(seg.search(1, 4, 5))#从根节点开始找，查找区间为[4,5]的区间和

🆗，over！