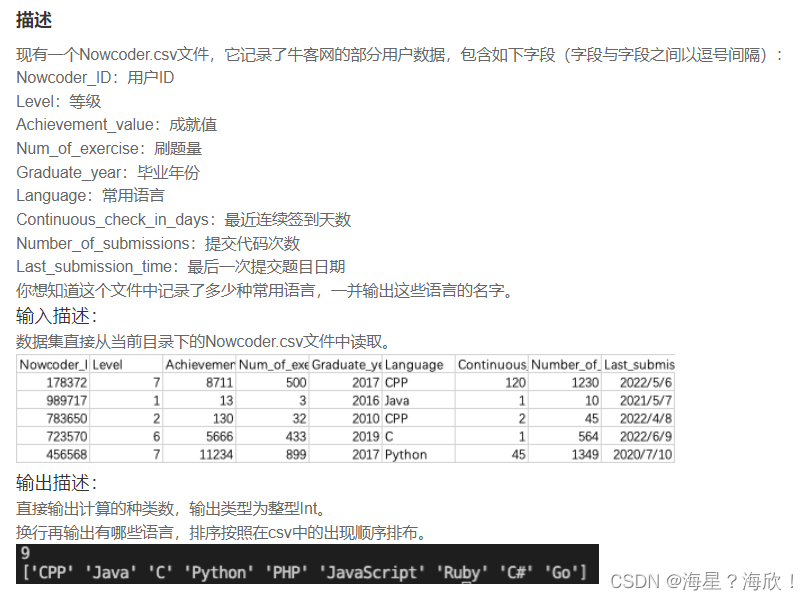
数据结构与算法（一）-软件设计（十七）
https://blog.csdn.net/ke1ying/article/details/129220378
- 线性表-队列与栈
队列：先进先出。
栈：先进后出。
循环队列：队投和队尾连接起来。
队空的条件：Head = tail。
队满的条件：(tail+1)%size =head。（因为为了区分队空 和 队满，留一个位置不让存储）
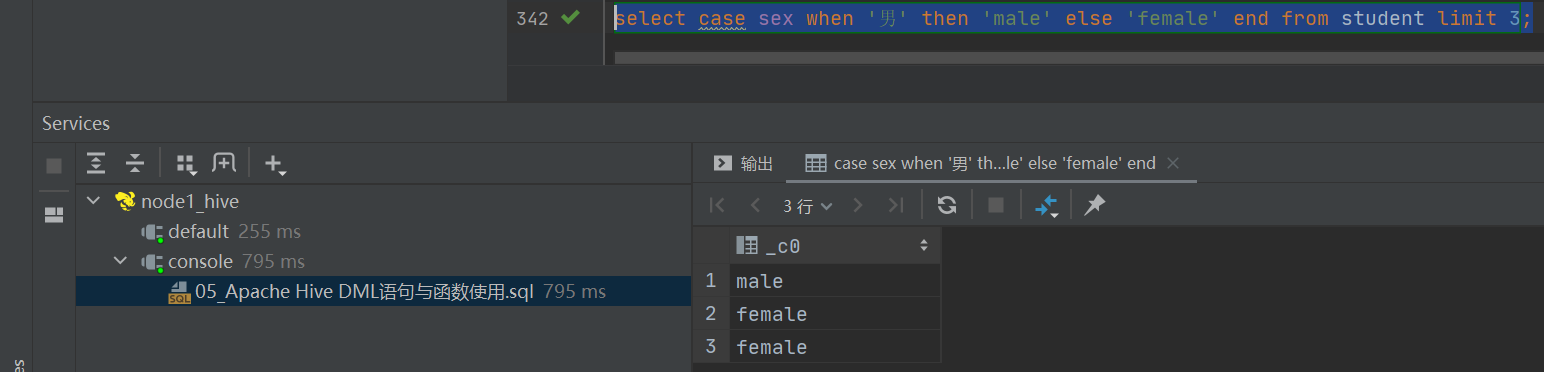
题目:元素按照a、b、c的次序进入栈，请尝试写出可能出栈的序列。
第一种情况：a进，a出，b进，b出，c进c出，所以abc。
第二种情况：a进，b进，b出，a出，c进，c出，所以bac。
第三种情况：a进，b进，c进，c出，b出，a出，所以cba。
- 广义表
广义表是n个表元素组成的有限序列，是线性表的推广。
通常用递归的形式进行标记，记作LS=（a0,a1....aN）。
例子：LS1 = (a,(b,c),(d,e))
注：LS1是表明表明，a0，a1等是他的表元素，它可以是子表，也可以是数据元素(原子)。
n是广义表的长度，LS1的长度是3：a,(b,c),(d,e)这三个
N=0则表示是空的广义表。
深度则就是括号的嵌套层数，LS1嵌套两层所以是2。
Head(LS1)=a。
Tail(LS1)=((b,c),(d,e))。
由此可见，表头是第一个元素，表尾是除了第一个元素的其他所有元素。
题目：有如上的广义表LS1，如何取出b元素？
- 取表尾得到((b,c),(d,e))
- 取表头得到(b,c)
- 取表头得到(b)
三、树与二叉树
树的基本概念
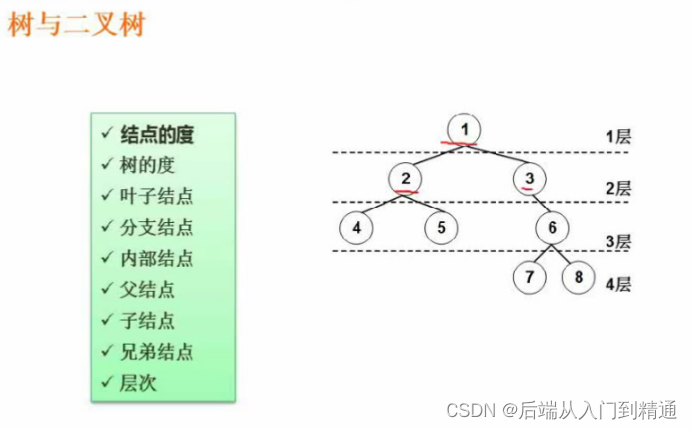
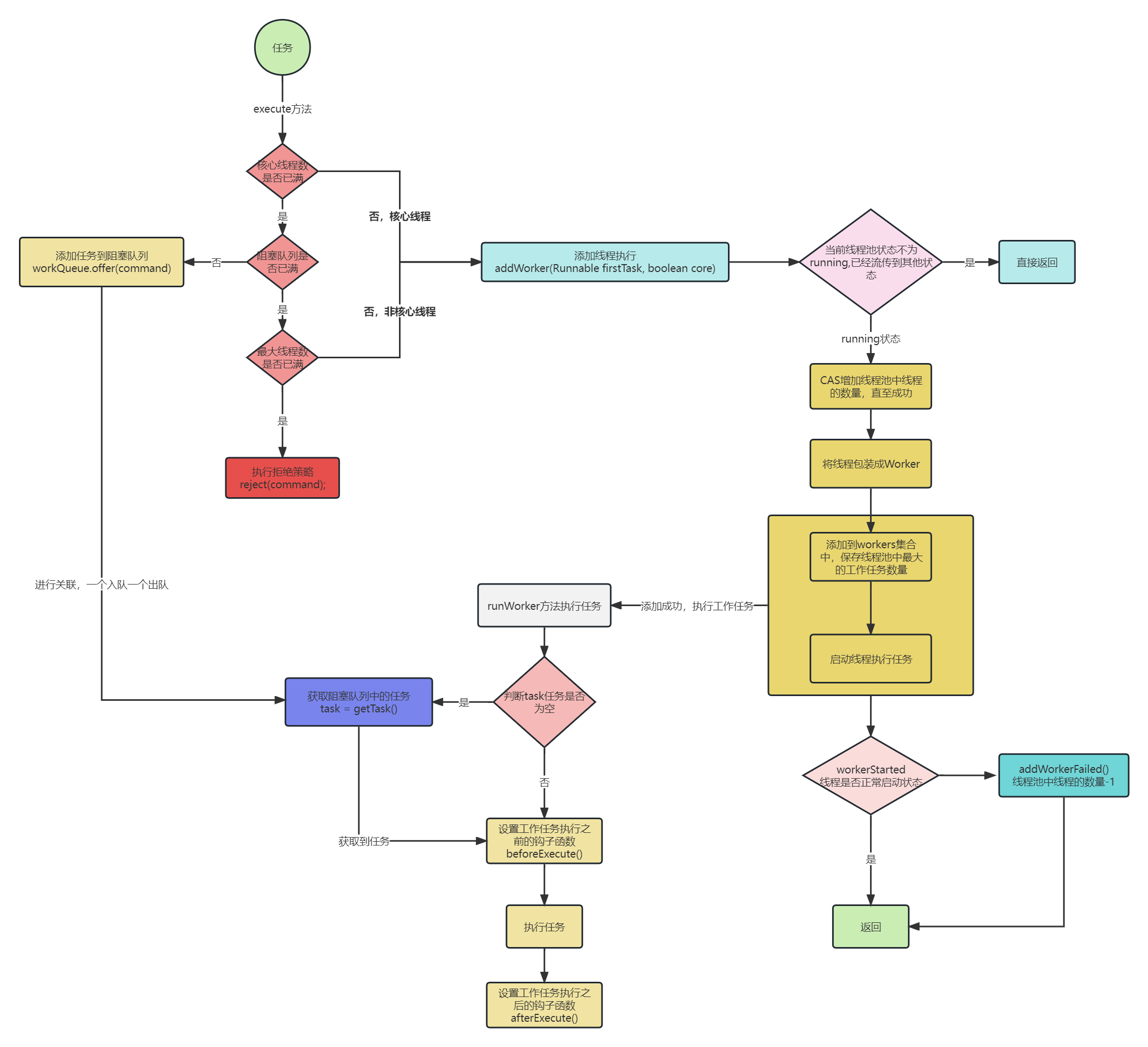
节点的度？
是某个节点的孩子节点个数，以节点1为例，有2和3两个孩子节点，所以1的节点度是2。
7号节点是叶子节点，则是0度。
树的度？
所有结点度数，最高的那个度就是 树的度，图上最高的度是2。
叶子结点？
4/5/7/8
分支结点？
有相应的分支。2/3/6
内部结点？
内部结点也是2/3/6
父结点？子节点？
对于2和4而言，2就是父结点，子节点是4
兄弟节点？
4/5，同一个父底下。
层次？
图上树是4层。
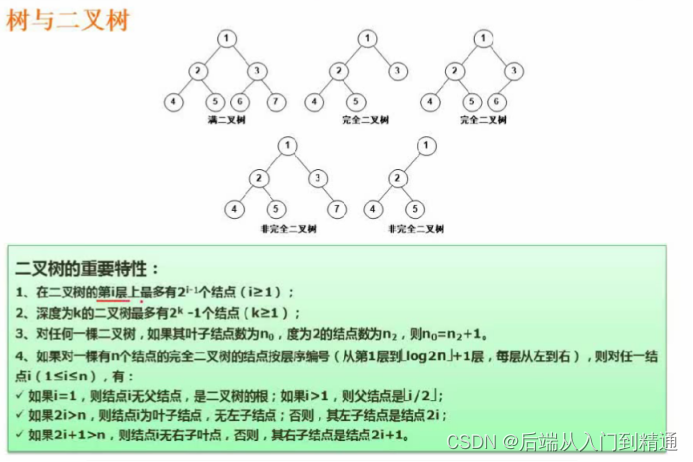
二叉树分为 满二叉树、完全二叉树、非完全二叉树。
他的重要特性有哪些？
- 在二叉树的第i层上最多有2的i-1个结点 (i>=1)。
- 深度为k的二叉树，最多有(2的k次方) - 1个结点(k>=1)。
- 对于任意一个二叉树，如果其叶子节点树为 x，度为2的节点数为 y，则x = y+1。
- 如果一颗树是完全二叉树，则会有如下定义
- 如果i=1，则结点i无父结点。如果i>1，则父结点是i/2。
(例子：6结点除以2他的父结点所以是3)
- 如果2i>n，则结点i为叶子结点，无左子结点，否则，其左子结点是结点2i。
（i=4的时候，2i = 8> n = 7，所以i是叶子节点，i=4无左子结点。
I=3的时候，2i = 6 < n =7，所以3的左子节点就是6）
- 如果2i+1>n，则结点i无右子叶点，否则，其右子结点是2i+1.
（当i=4时候，2i+1 = 9>n = 7，所以4无右子叶点，
当i=2时候，2i+1=5<7，所以2的右子结点时 5）
四、二叉树的遍历
前序遍历、中序遍历、后序遍历、层次遍历。
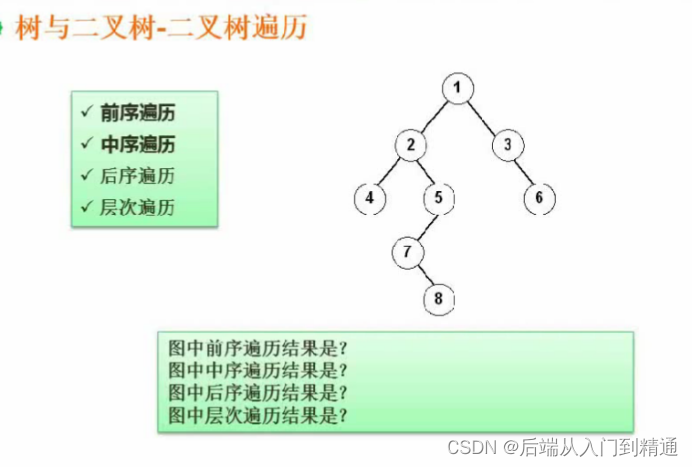
层次遍历：12345678
前序遍历：根结点，左子树，右子树
1 24578 36
（因为左子树结点里根是2，所以从2开始。）
中序遍历：左子树，根，右子树
42785 1 36
(为什么是42785呢？
因为中序是从左子树开始访问，
第一步：2为根的左子树是4，所以42
第二步：5为根的左子树是78，所以785)
后序遍历：
48752 63 1
区别就是前序每次统计以根结点为主。
中序和后续每次统计以左结点为主。
反向构造二叉树一般是给出前序中序一起，让反向推导出二叉树是什么样子。
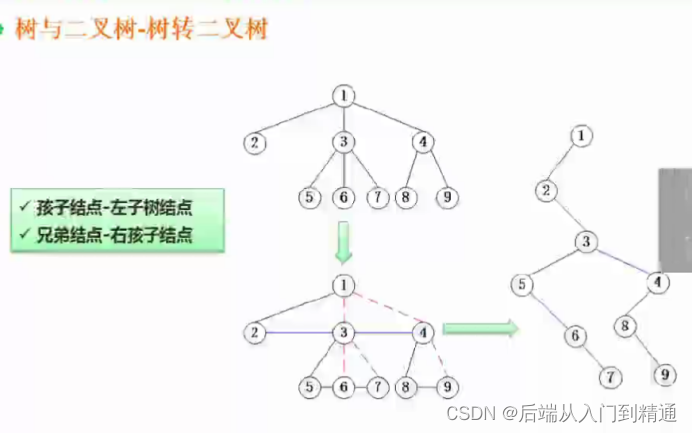
树转二叉树：孩子结点-左子树结点；兄弟结点-右孩子节点。
- 查找二叉树（排序二叉树）
左子树小于根结点，右子树大于根结点的树，就是查找二叉树。
插入结点：
- 若该结点已存在，则不再插入。
- 若树为空，则该结点时根结点。
- 若树不空，则与根结点比较，小于放在左子树，大于放右子树。
删除结点：
- 若是叶子结点，直接删除。
- 若删除结点下有一个结点，则把下面的结点直接移动上来。
- 若删除的结点有两个子结点，则在其左子树，找到最大的结点移动上来。然后按照2的步骤删除找到的结点。
