---

欢迎访问个人网络日志🌹🌹知行空间🌹🌹

---

1.基础介绍

论文：Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks

这是2006年第23次ICML会以上的一篇论文。

很多实际应用需要从未切分的数据中输出序列信息，如语音识别中的语音转文字,光学字符识别(Optical character recognition,OCR)中的字符图片转字符序列。循环神经网络(Recurrent neural networks,RNN)十分适合序列数据的学习，但其训练数据要求必须是切分后的序列，而实际应用中切分的训练序列数据标注比较困难，是很难获取的。

上图是OCR的两种模型，一种如图(a)可直接输入OCR检测得到的图片得到图片中的字符串can，另外一种需要先将图片按字符进行切割，这种方式比较数据处理比较复杂，而这种正是循环神经网络RNN要求的输入。

为了充分利用循环神经网络RNN处理序列数据的能力，同时避免对输入序列图像进行切分，本文作者提出了Connectionist Temporal Classificatio(CTC)算法。

2.Connectionist Temporal Classification(CTC)算法

2.1 什么是Temporal Classification

$S$是从分布${\mathcal{D}}_{\mathcal{X}\times \mathcal{Z}}$从获取的训练数据，
输入空间$\mathcal{X}=({\mathbb{R}}^m{)}^{\ast }$是$m$维的实值向量序列，目标空间$\mathcal{Z}=L^{\ast }$由字母集$L$组成的标签序列，训练数据集$S$中的每个样本由序列对$(\mathbf{x},\mathbf{z})$组成。目标序列$\mathbf{z}=(z_1,z_2,...,z_U)$长度小于等于输入序列$\mathbf{x}=(x_1,x_2,...,x_T),i.e.U\le T$。输入序列和输出序列长度一般不同，因此没有先验知识可以对齐他们。

Temporal Classification的任务是使用训练数据$S$,学习一个分类器，能够将输入序列分成对应的目标序列$h:\mathcal{X}\to \mathcal{Z}$

从第一部分介绍，可以知道OCR任务本身就是一个Temporal Classification，翻译成了时间序列分类问题。其输入是卷积后得到特征图序列，输出的是字符序列。

之所以被称为Connectionist Temporal Classification，是这样理解的，原始输入的是一整张联结在一起未切分的字符图像，输出的是字符序列，因为没有对原始图像上的字符进行切分预处理，因此被称之为连接序列分类。

2.2 CTC问题描述

从网络输入到获取标签序列要分成两步：

第一步，可以将输入为长度为$T$的序列$\mathbf{x}=[x_1,x_2,...,x_T]$(序列中每个$x$都是m维),输出为长度$T$的序列$\mathbf{y}=[y_1,y_2,...,y_T]$(序列中每个$y$都是n维),参数为$w$的映射(即循环神经网络)定以为${\mathcal{N}}_w:({\mathbb{R}}^m{)}^T\to ({\mathbb{R}}^n{)}^T$，$\mathbf{y}={\mathcal{N}}_w(\mathbf{x})$。将$y_k^t$表示成第$t$个序列值为$k$的概率，$L^{\prime T}$表示长度为$T$的序列,其中每个元素取自字母集 L ′ = L ∪ { b l a n k } L'=L\cup\{blank\} L′=L∪{blank}，序列$L^{\prime T}$也被称之为路径，表示成$\pi$。

根据以上定义给定输入$\mathbf{x}$,输出为路径$\pi$的概率可表示成：

$$p(\pi |\mathbf{x})=\prod _{t=1}^T{y}_{{\pi }_t}^t,\forall \pi \in L^{\prime T}$$

其实，这里还有个条件，就是每一步输出之间是相互独立，上面的公式才能成立。

第二步，我们知道输入$\mathbf{x}$对应的标签序列为长度等于$U$的序列$\mathbf{z}=[z_1,z_2,...,z_U]，U\le T$,在第一步中循环神经网络给出的只是长度为$T$的中间序列$\mathbf{y}$,要和长度为$U$的标签序列$\mathbf{z}$对应，还需要定义个从中间序列到标签序列的映射$\mathcal{B}:L^{\prime T}\mapsto L^{<T}$,很明显，$\mathcal{B}$是一个多对一的映射。这个映射可以定义为移除中间序列中的重复相邻字符和空格占位符，如$\mathcal{B}(s-ta-tt-e)=\mathcal{B}(s-t-aa-tt-e)=state$,定义了映射$\mathcal{B}$后，可以将输出标签序列$\mathbf{z}$的后验概率表示成：

$$p(\mathbf{z}|\mathbf{x})=\sum _{\pi \in {\mathcal{B}}^{-1}(\mathbf{z})}p(\pi |\mathbf{x})$$

2.2关于对齐

为什么要使用上述的方法来进行网络的训练呢？那是因为输入$\mathbf{x}=[x_1,x_2,...,x_m]$和标签序列$\mathbf{z}=[z_1,z_2,...,z_U]$之间在序列长度，序列长度比例，对应元素之间找不到什么对应关系。

如上图是对齐后的数据，但在实际中是很难知道$(x_1,x_2)\mapsto c,(x_3,x_4,x_5)\mapsto a,(x_6)\mapsto t$,标注这样的数据也需要花费大量的时间，因此更希望模型能够拥有从未对齐数据中学习的能力，通过前面的介绍，使用CTC算法可以从未对齐的输入中求得标签序列。

2.3 前向后向算法

使用暴力方法计算

$$p(\mathbf{z}|\mathbf{x})=\sum _{\pi \in {\mathcal{B}}^{-1}(\mathbf{z})}p(\pi |\mathbf{x})$$

因为要计算每一条路径，因此对于序列字典中有$n$个元素，长度为$T$的序列，要计算所有路径的概率，时间复杂度为$O(n^T)$，这是指数级的时间复杂度，对于大部分长度的序列这个运算都过于耗时。论文作者为了解决这个问题，提出了前向后向递推算法，采用动态规划的方法将时间复杂度降到了$O(nT)$,使算法更可行。

先借个例子来看一下。

假设标签序列为
$$\mathbf{z}=state$$

在序列前后和每个字符中间添加空格占位符$-$：

$${\mathbf{z}}^{\prime }=-s-t-a-t-e-$$

对${\mathbf{z}}^{\prime }$中任意的字符重复任意次，经过$\mathcal{B}$映射都能得到标签序列$state$，因此可以将${\mathbf{z}}^{\prime }$当成满足变换条件的基础序列。$\mathcal{B}$是多对一的映射，如下4个路径都能得到$state$

$$\begin{gathered} \mathcal{B}(--sttaa-tee-)=state \\ \mathcal{B}(--stta-t---e)=state \\ \mathcal{B}(sst-aaa-tee-)=state \\ \mathcal{B}(sst-aa-t---e)=state \end{gathered}$$

将${\mathbf{z}}^{\prime }$写成列的形式，则上述四条路径可以写成如下图的形式：

从上图可以看到，四条路径在序列$t=6$时都经过字符$a$,记上面的四条路径为${\pi }^1,{\pi }^2,{\pi }^3,{\pi }^4$

π 1 = b = b 1 : 5 + { a } 6 + b 7 : 12 π 2 = r = r 1 : 5 + { a } 6 + r 7 : 12 π 3 = b 1 : 5 + { a } 6 + r 7 : 12 π 4 = r 1 : 5 + { a } 6 + b 7 : 12 \pi^1=b=b_{1:5}+\{a\}_6+b_{7:12}\\ \pi^2=r=r_{1:5}+\{a\}_6+r_{7:12}\\ \pi^3=b_{1:5}+\{a\}_6+r_{7:12}\\ \pi^4=r_{1:5}+\{a\}_6+b_{7:12} π1=b=b1:5​+{a}6​+b7:12​π2=r=r1:5​+{a}6​+r7:12​π3=b1:5​+{a}6​+r7:12​π4=r1:5​+{a}6​+b7:12​

记$y_k^t$表示序列第$t$步元素为$k$的概率，则上面四条路径都包含$y_a^6$这一项，将计算上面四条路径的概率表示可以提取公因式写成：

$$\begin{gathered} foward=p(b_{1:5}+r_{1:5}|\mathbf{x})=y_{-}^1\ast y_{-}^2\ast y_s^3\ast y_t^4\ast y_t^5+y_s^1\ast y_s^2\ast y_t^3\ast y_{-}^4\ast y_a^5 \\ backward=p(b_{7:12}+r_{7:12}|\mathbf{x})=y_{-}^7\ast y_t^8\ast y_{-}^9\ast y_{-}^{10}\ast y_{-}^{11}\ast y_e^{12}+y_a^7\ast y_{-}^8\ast y_t^9\ast y_e^{10}\ast y_e^{11}\ast y_{-}^{12} \end{gathered}$$

然后上面四条路径的概率和可以写成：

$$p({\pi }^1,{\pi }^2,{\pi }^3,{\pi }^4|\mathbf{x})=forward\ast y_a^6\ast backward$$

上面的介绍中只取了四条经过变换$\mathcal{B}$后能得到$state$的路径，实际上的路径要远远多于此：

从上图中选出经过 { a } 6 \{a\}_6 {a}6​的所有路径，概率$\sum _{\mathcal{B}(\pi )=\mathbf{z},{\pi }_6=a}p(\pi |x)$(${\pi }_6=a$表示路径$\pi$的第6个字符为a),同样还是可以表示成如下形式:

$\sum _{\mathcal{B}(\pi )=\mathbf{z},{\pi }_6=a}p(\pi |x)=forward\ast y_a^6\ast backward$

进一步推广，定义${\alpha }_t(s)$表示路径$\pi$中的第t个字符与加了占位符后标签序列$z^{\prime }$的第s个字相对应且路径$\pi$满足$\mathcal{B}({\pi }_{1:t})={\mathbf{z}}_{1:s}$时所有路径${\pi }_{1:t}$的概率和,表示成：

$${\alpha }_t(s)=\sum _{\mathcal{B}({\pi }_{1:t})\stackrel{留-}{=}{\mathbf{z}}_{1:s}^{\prime }}\prod _{t^{\prime }=1}^t{y}_{{\pi }_{t^{\prime }}}^{t^{\prime }}$$

可以看到这等同于前向变量$forward$，现在来看$t=1$时的${\alpha }_1(s)$,要经过$\mathcal{B}$映射后能得到保留占位符的标签序列，$s$就只能等于1或者2，看上图中$-s-t-a-t-e-$的例子，t=1时刻只能取$z^{\prime }$的$-$或者$s$,否则无法经过$\mathcal{B}$映射得到标签序列，因此

$$\begin{gathered} {\alpha }_1(1)=y_{-}^1 \\ {\alpha }_1(2)=y_{{\mathbf{z}}_2^{\prime }}^1 \\ {\alpha }_1(s)=0,\forall s>2 \end{gathered}$$

还看$state$的例子，当过${{\mathbf{z}}^{\prime }}_6$时，$t=5$对应的字符只能是$t/-/a$,可以推出来上面例子中

$${\alpha }_6(6)=({\alpha }_5(4)+{\alpha }_5(5)+{\alpha }_5(6))\ast y_a^6$$
一般化推广可得：

$${\alpha }_t(s)=({\alpha }_{t-1}(s-2)+{\alpha }_{t-1}(s-1)+{\alpha }_{t-1}(s))\ast y_{{\mathbf{z}}_s^{\prime }}^t$$

还需考虑一个特殊情况，看下面例子$\mathbf{z}=zoo,{\mathbf{z}}^{\prime }=-z-o-o-$,t=2,s=6或3:

很明显因为$\mathcal{B}$映射会去除重复的字母，因此上面两种情况在$t-1$时刻不能取$s-2$

综上，可得最终$t\ge 2$时前向递推公式为(也就是原论文上的递推公式)：

$${\alpha }_t(s)=\{\begin{array}{c}({\alpha }_{t-1}(s-1)+{\alpha }_{t-1}(s))\ast y_{{\mathbf{z}}_s^{\prime }}^{t}if{z}_s^{\prime }=-or{z}_s^{\prime }=z_{s-2}^{\prime }\\ ({\alpha }_{t-1}(s-2)+{\alpha }_{t-1}(s-1)+{\alpha }_{t-1}(s))\ast y_{{\mathbf{z}}_s^{\prime }}^{t}otherwise\end{array}$$

将公式中相同的项合并一下就可以得到论文上的公式了。

同样的方法可以定义$backward$:

$${\beta }_t(s)=\sum _{\mathcal{B}({\pi }_{t:T})\stackrel{留-}{=}{\mathbf{z}}_{s:|z^{\prime }|}^{\prime }}\prod _{t^{\prime }=t}^T{y}_{{\pi }_{t^{\prime }}}^{t^{\prime }}$$

$t\ge 2$时${\beta }_t(s)$的递推公式：

$${\beta }_t(s)=\{\begin{array}{c}({\beta }_{t+1}(s)+{\beta }_{t+1}(s+1))\ast y_{{\mathbf{z}}_s^{\prime }}^{t}if{z}_s^{\prime }=-or{z}_s^{\prime }=z_{s+2}^{\prime }\\ ({\beta }_{t+1}(s)+{\beta }_{t+1}(s+1)+{\beta }_{t+1}(s+2))\ast y_{{\mathbf{z}}_s^{\prime }}^{t}otherwise\end{array}$$

求得${\alpha }_t(s)$和${\beta }_t(s)$后，标签序列$\mathbf{z}$的后验概率可以写成，

$$p(\mathbf{z}|\mathbf{x})=\sum _{z_s^{\prime }\in {\pi }_t}\frac{{\alpha }_t(s){\beta }_t(s)}{y_{z_s^{\prime }}^t}$$

求得$p(\mathbf{z}|\mathbf{x})$后，可以知道使用$CTC$时的目标就是最大化$p(\mathbf{z}|\mathbf{x})$,可以定义损失函数为$-log(p(\mathbf{z}|\mathbf{x}))$，可以推导损失的计算和损失函数梯度都能使用递推的方式来计算，减少运算量，加快运算速度。

2.4 推理时

训练完成后，在网络推理时希望取概率最大的输出序列：

$${\mathbf{z}}^{\ast }=\underset{\mathbf{z}}{\mathrm{argmax}}p(\mathbf{z}|\mathbf{x})$$

对所有路径的概率求和，然后取概率最大的路径作为预测的结果，应该是最合理的方式，但当序列比较长时面临计算量过大，影响推理速度的情况。

一种做法是对于第$t$步，取概率最大的字符，然后将所有的字符组合起来经过去重当作最终的输出，但这种做法只考虑了一条路径，有可能有多条路径对应标签，各条路径的概率加和后有可能更大。

一种替代的折衷方法是改进版的Beam Search。

常规的Beam Search算法，对于每个时间步取概率最大的几个(Beam Size)可能结果，如下为字母集为$-,a,b$，Beam Size=3的Beam Search的过程：

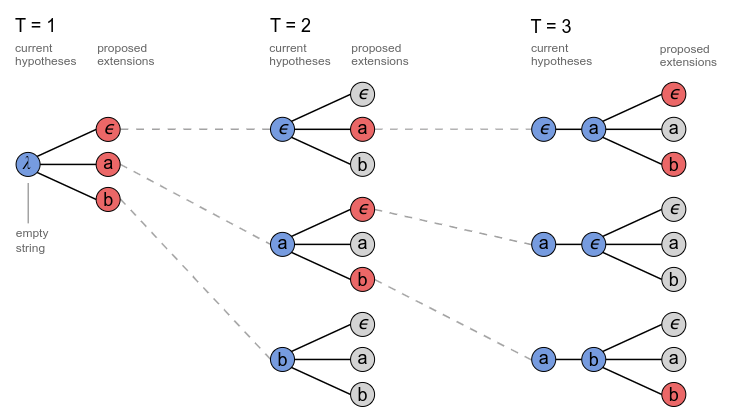
上图中Beam Search到当前步最大的几个(Beam Size)可能字符都只有一条前缀序列，实际上可以有多条前缀序列和当前的字符组合后都得到相同的输出，如下图对于路径长度$T=2$时$\lambda a$,$a-$,$aa$最后都能对应的$a$

且观察$T=3$时，前缀序列$aa$对应的输出有可能是$a$或者$aa$,因此对应的概率应该分别进行计算。

3.pytorch中的CTCLOSS

计算未切分的连续时间序列和目标序列之间的损失。

torch.nn.CTCLoss(blank=0, reduction='mean', zero_infinity=False)

class CTCLoss:
     ...
     def forward(self, log_probs: Tensor, targets: Tensor, input_lengths: Tensor, target_lengths: Tensor) -> Tensor:
          ...
     

• log_probs：Tensor of size (T,N,C)/(T,C),T是输入长度，N是Batch Size，C是序列字典的大小(包括空格)

• targets：Tensor of size（N，S）N是batch size，S是最大目标序列长度，目标序列中的每个元素是类别的序号。

• input_lengths，每个输入序列的长度，为元组tuple或shape为(N,)的张量，N是batch size，input_lengths的值$\le T$

• target_lengths,每个目标序列的长度，为元组tuple或shape为(N,)的张量，N是batch size，如果targets的shape是(N,S),这里其实是把每个$target$添加padding后变成了S，假设第n个序列目标长度为$s_n$,target_lengths中第n个元素值就为$s_n$。

import torch

T = 2
C = 3
N = 1
S = 2
S_min = 1

input = torch.randn(T,N,C).log_softmax(2).detach().requires_grad_()
print(input)
target = torch.tensor([0,1], dtype=torch.long).reshape(shape=(N, S))
print(target)
input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.tensor([2], dtype=torch.long).reshape(shape=(N,)) 
ctc_loss = torch.nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
print(loss)

# tensor([[[-0.4002, -1.5314, -2.1752]],         [[-0.8444, -2.2039, -0.7770]]], requires_grad=True)
# tensor([[0, 1]])
# tensor(1.3021, grad_fn=<MeanBackward0>)

上面示例的计算过程：

从上图可以看到目标是$01$即at路径有且仅有此一条，损失值计算为：

$$loss=-\frac{1}{2}[-0.4002+(-2.2039)]=1.3021$$

---

欢迎访问个人网络日志🌹🌹知行空间🌹🌹

---

参考资料

• 1.https://distill.pub/2017/ctc/
• 2.https://zhuanlan.zhihu.com/p/161186907
• 3.https://zhuanlan.zhihu.com/p/519960905
• 4.https://zhuanlan.zhihu.com/p/58526617