Python蓝桥杯训练:基本数据结构 [哈希表]
文章目录
- Python蓝桥杯训练:基本数据结构 [哈希表]
- 一、哈希表理论基础知识
- 1、开放寻址法
- 2、链式法
- 二、有关哈希表的一些常见操作
- 三、力扣上面一些有关哈希表的题目练习
- 1、[有效的字母异位词](https://leetcode.cn/problems/valid-anagram/)
- 2、[两个数组的交集](https://leetcode.cn/problems/intersection-of-two-arrays/)
- 3、[快乐数](https://leetcode.cn/problems/happy-number/)
- 4、[两数之和](https://leetcode.cn/problems/two-sum/)
- 5、[四数相加Ⅱ](https://leetcode.cn/problems/4sum-ii/)
- 6、[三数之和](https://leetcode.cn/problems/3sum/)
- 7、[四数之和](https://leetcode.cn/problems/4sum/)
- 四、如何选择哈希表实现对象?
本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG,持续更新中,另外这是我创建的编程学习小组频道,想一起学习的朋友可以一起!!!
一、哈希表理论基础知识
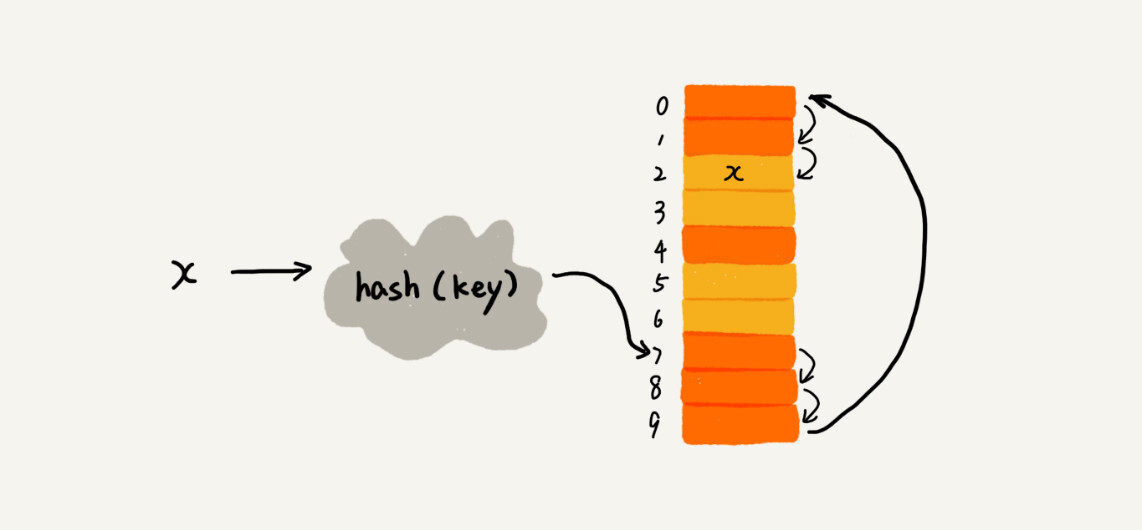
哈希表(Hash table)是一种常用的数据结构,它通过使用哈希函数将数据元素映射到数组中的某个位置,并使用链表维护元素间的映射关系。哈希表具有查询、插入、删除等操作的高效性,因此被广泛应用于数据存储、查找和删除等场景。
哈希函数(Hash function)是哈希表的核心部分,它通过一种特定的映射方式,将数据元素映射到数组的某个位置上。一般来说,哈希函数需要满足以下三个条件:
- 哈希函数对于任意的数据元素,都能生成一个数组下标;
- 对于不同的数据元素,生成的下标尽可能不同;
- 对于相同的数据元素,生成的下标始终相同。
如果哈希函数生成的下标相同,我们称之为哈希冲突(Hash collision)。哈希冲突的处理方式有很多种,常见的有开放寻址法和链式法。
1、开放寻址法
当冲突发生时,在下一个空余的位置存储该数据元素。
开放寻址法的思想是当哈希冲突发生时,继续寻找数组中下一个空闲的位置,并将数据元素插入该位置。具体来说,开放寻址法中有三种常用的冲突解决方法:
- 线性探测(Linear Probing):当哈希冲突发生时,以步长为1,在数组中寻找下一个空闲的位置,并将数据元素插入该位置。
- 二次探测(Quadratic Probing):当哈希冲突发生时,以步长的平方为增量,在数组中寻找下一个空闲的位置,并将数据元素插入该位置。
- 双重哈希(Double Hashing):当哈希冲突发生时,使用第二个哈希函数计算出步长,并在数组中寻找下一个空闲的位置,并将数据元素插入该位置。
优点:
- 对于小规模数据集,开放寻址法具有较小的空间开销;
- 开放寻址法的数据存储在数组中,因此具有较好的局部性,缓存命中率高。
缺点:
- 开放寻址法对于冲突的解决方式较为固定,不具有链式法灵活的处理方式;
- 随着数据集的扩大,开放寻址法容易出现聚集现象,即数据元素的分布不均匀,从而导致探测冲突的频率增加,插入和查找效率降低。
应用场景:
- 适用于小规模数据集,并且需要快速随机访问的场景。
2、链式法
链式法的思想是当哈希冲突发生时,在该位置存储一个链表,并将该数据元素插入链表中。链式法的实现相对简单,具体来说,可以使用数组和链表组合实现,即数组中每个位置存储一个指向链表头节点的指针。
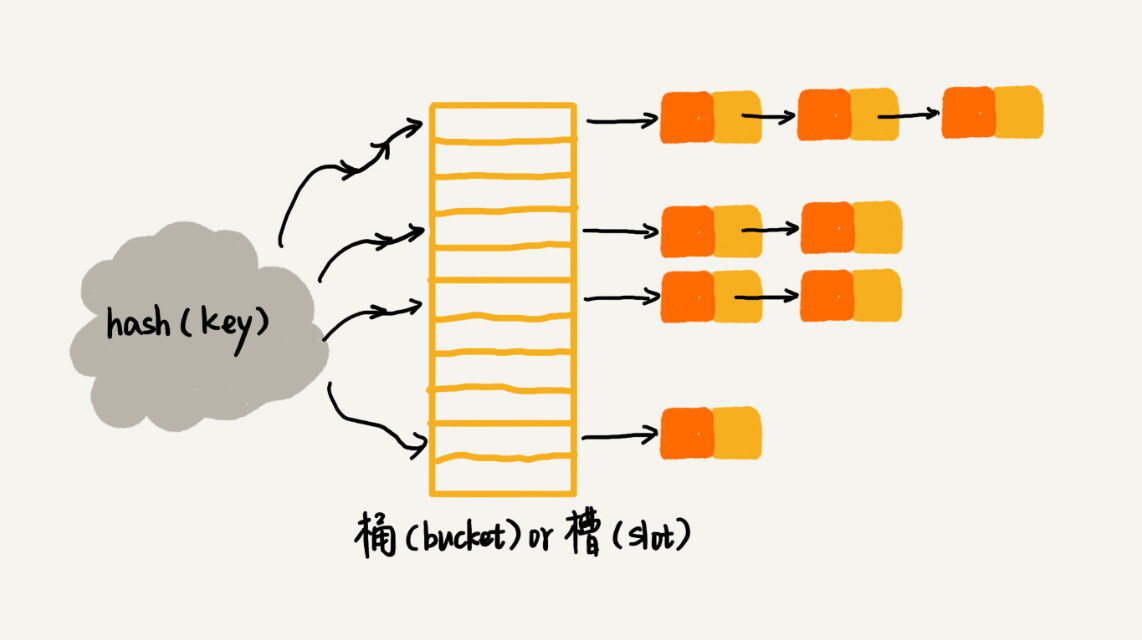
优点:
- 链式法的数据存储在链表中,因此对于大规模数据集,可以有效地解决聚集现象,具有较好的扩展性;
- 链式法的处理方式较为灵活,能够处理各种类型的哈希冲突。
缺点:
- 链式法的链表节点需要额外的空间存储指针信息,因此对于空间的使用有一定的额外开销;
- 链式法的查询效率取决于链表的长度,因此如果链表过长,查询效率会降低。
应用场景:
- 适用于大规模数据集,并且需要支持高效插入和删除操作的场景。
开放寻址法和链式法都是哈希表解决哈希冲突的有效方法。在选择哪种方法时,需要考虑数据集大小、查询、插入和删除操作的需求以及空间的限制等因素。在实际应用中,常常需要根据实际情况选择适合的哈希表实现方式。
哈希表的查询、插入、删除等操作都是基于哈希函数的。查询操作是通过计算出该数据元素的哈希值,并在数组中找到对应的位置,如果该位置存在该数据元素,则返回该数据元素。插入操作是在查询操作的基础上,在数组中的对应位置插入该数据元素。删除操作是通过查询操作找到该数据元素,并在数组中删除该数据元素。
总的来说,哈希表是一种高效的数据存储和查询结构,它通过使用哈希函数和链表维护数据元素之间的映射关系,在提高数据存储和查询效率的同时,也具有解决哈希冲突的能力。
二、有关哈希表的一些常见操作
Python 中的哈希表实现是通过内置的 **dict**数据类型实现的。下面是一些常见的哈希表操作及其对应的 Python 代码:
-
插入元素
使用 **
dict[key] = value**进行插入,如果 key 已经存在,会将对应的 value 进行更新。d = {} d["key1"] = "value1" d["key2"] = "value2" d["key1"] = "new_value1" # 更新 key1 对应的值 -
删除元素
使用 **
del dict[key]**进行删除操作,如果 key 不存在,会抛出 KeyError 异常。d = {"key1": "value1", "key2": "value2"} del d["key1"] -
查询元素
使用 **
dict[key]**进行查询操作,如果 key 不存在,会抛出 KeyError 异常。d = {"key1": "value1", "key2": "value2"} value = d["key1"] -
判断元素是否存在
可以使用 **
key in dict**来判断 key 是否存在于 dict 中。d = {"key1": "value1", "key2": "value2"} if "key1" in d: print("key1 exists in the dictionary") -
遍历元素
可以使用 **
for key in dict**来遍历 dict 中的所有 key,也可以使用dict.items()方法来遍历 dict 中的所有键值对。d = {"key1": "value1", "key2": "value2"} for key in d: print(key, d[key]) for key, value in d.items(): print(key, value)
三、力扣上面一些有关哈希表的题目练习
1、有效的字母异位词
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例1:
输入: s = "anagram", t = "nagaram"
输出: true
示例2:
输入: s = "rat", t = "car"
输出: false
提示:
1 <= s.length, t.length <= 5 * 10^4
s 和 t 仅包含小写字母
进阶: 如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
1、字典计数:将两个字符串都转化为字典,然后比较这两个字典是否相等。字典中 key 为字符串中的字符,value 为字符出现的次数。
2、排序:对两个字符串分别进行排序,然后比较两个有序字符串是否相等。
3、哈希表:使用长度为 26 的数组记录每个字符出现的次数,然后比较两个数组是否相等。
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
if len(s) != len(t):
return False
dict_s = {}
dict_t = {}
for char in s:
dict_s[char] = dict_s.get(char, 0) + 1
for char in t:
dict_t[char] = dict_t.get(char, 0) + 1
return dict_s == dict_t
该算法的时间复杂度为 O(n),空间复杂度为 O(n)。
方法二:
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
return sorted(s) == sorted(t)
该算法的时间复杂度为 O(nlogn),空间复杂度为 O(n)(由于排序需要使用额外的空间)。
方法三:
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
record = [0] * 26
for i in s:
record[ord(i) - ord('a')] += 1
for i in t:
record[ord(i) - ord('a')] -= 1
for i in range(26):
if record[i] != 0:
return False
return True
该算法的时间复杂度为 O(n),空间复杂度为 O(1)。由于字符串中只包含小写字母,因此数组的长度为 26。
B站上面卡尔老师对于这道题的解题思路是使用哈希表解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1YG411p7BA/?spm_id_from=333.788&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
2、两个数组的交集
示例1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的
提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000
class Solution:
def intersection(self, nums1, nums2):
# 创建一个空的哈希表
val_dict = {}
# 创建一个空的结果列表
ans = []
# 遍历数组 nums1 中的元素,将其作为哈希表中的键,对应的值设置为 1
for num in nums1:
val_dict[num] = 1
# 遍历数组 nums2 中的元素
for num in nums2:
# 如果当前元素在哈希表中存在且对应的值为 1
if num in val_dict.keys() and val_dict[num] == 1:
# 将当前元素加入结果列表 ans 中
ans.append(num)
# 将哈希表中对应的值设置为 0,以便去重
val_dict[num] = 0
# 返回结果列表 ans
return ans
这段代码的时间复杂度同样为 O(m+n),其中 m 和 n 分别为两个数组的长度。
需要注意的是,这段代码中使用了字典的 **keys()**方法来判断某个键是否存在于字典中,但实际上可以直接使用 if num in val_dict:来判断某个键是否存在于字典中,因为在 Python 中,in
操作符默认会在字典的键中查找。另外,在这段代码中,将哈希表中对应的值设置为 0 是为了去重,但实际上不需要这么做,可以直接使用 set 数据类型来实现去重,这样代码会更简洁。
下面是体现Python之美的简洁代码:
class Solution:
def intersection(self, nums1, nums2):
nums1 = set(nums1)
nums2 = set(nums2)
return list(nums1 & nums2)
更简洁的写法是:
class Solution:
def intersection(self, nums1, nums2):
return list(set(nums1) & set(nums2))
如果我们使用暴力枚举法的话,我们可以枚举数组 **nums1**和 **nums2**中的每个元素,判断它们是否相等,如果相等就加入结果集中。具体实现代码如下:
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
ans = []
for num1 in nums1:
for num2 in nums2:
if num1 == num2 and num1 not in ans:
ans.append(num1)
return ans
这段代码的时间复杂度为 O(mn),其中 m 和 n 分别为两个数组的长度。由于需要对结果集去重,因此还需要额外的时间复杂度,所以使用暴力解法不如使用哈希表或 set 数据类型来实现高效。
B站上面卡尔老师对于这道题的解题思路是使用第一种详细的哈希表法解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1ba411S7wu/?spm_id_from=333.788&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
3、快乐数
「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
哈希表法的基本思路是,对于一个数字 n,我们按照题目要求进行一系列计算得到一个新的数字 m,然后将 m 保存在哈希表中。如果计算后得到的数字 m 已经在哈希表中出现过了,那么说明我们已经进入了一个循环,这个数不是快乐数。否则,我们继续按照题目要求进行计算,直到得到 1 或者进入循环。
这道题同样可以使用暴力枚举法解决,我们需要不断地按照题目要求计算,直到得到 1 或者进入循环。具体来说,我们可以编写一个计算平方和的函数 squareSum,然后在一个 while 循环中不断调用这个函数,直到得到 1 或者进入循环。在每一轮计算中,我们将当前数字赋值给 n,然后调用 squareSum 计算出一个新的数字 m。如果 m 等于 1,说明这个数是快乐数;否则,我们继续按照题目要求计算,直到得到 1 或者进入循环。
class Solution:
def isHappy(self, n):
seen = set() # 用来保存已经出现过的数字
while n != 1 and n not in seen:
seen.add(n)
n = sum(int(i) ** 2 for i in str(n))
return n == 1
在上面代码中,我们首先定义了一个空的集合 seen,用来保存已经出现过的数字。然后,我们使用一个 while 循环来按照题目要求进行计算,直到得到 1 或者进入循环。在每一轮计算中,我们首先将当前数字 n 加入到 seen 中,然后按照题目要求计算出一个新的数字 m,并将 m 赋值给 n。如果 n 已经出现在 seen 中了,那么说明我们进入了一个循环,可以直接退出循环。最后,我们判断 n 是否等于 1,如果是,返回 True,否则返回 False。
我们还可以换一种实现思路,但还是使用的哈希表法,那就是使用哈希表来记录出现过的数字,每次计算平方和后判断是否出现过,如果出现过则说明出现了循环,否则继续计算。具体来说,代码定义了一个函数 calculate_happy,用来计算一个数每个位置上的数字的平方和。然后,使用一个 **set**类型的哈希表 **record**来记录已经出现过的数字,初始时 **record**是空的。接下来,我们进入一个 while 循环,不断计算 **n**的平方和并更新 **n**的值,直到 **n**等于 1 或者 **n**在 **record**中出现过。在每一轮循环中,我们首先调用 **calculate_happy**计算出 **n**的平和,然后判断平方和是否等于 1,如果是,说明这个数是快乐数,可以直接返回 True。如果平方和在 **record**中出现过,说明我们已经进入了一个循环,可以直接返回 False。否则,将平方和加入到 **record**中,并将 **n**赋值为平方和,继续循环。
具体实现代码如下:
class Solution:
def isHappy(self, n):
# 定义一个函数,用来计算一个数每个位置上的数字的平方和
def calculate_happy(num):
sum_ = 0
while num:
sum_ += (num % 10) ** 2
num = num // 10
return sum_
# 定义一个 set 类型的哈希表 record,用来记录已经出现过的数字
record = set()
# 进入一个 while 循环,不断计算 n 的平方和并更新 n 的值,直到 n 等于 1 或者 n 在 record 中出现过
while True:
# 计算 n 的平方和
n = calculate_happy(n)
# 如果 n 等于 1,说明这个数是快乐数,可以直接返回 True
if n == 1:
return True
# 如果平方和在 record 中出现过,说明我们已经进入了一个循环,可以直接返回 False
if n in record:
return False
# 否则,将平方和加入到 record 中,并将 n 赋值为平方和,继续循环
else:
record.add(n)
如果我们使用暴力枚举法解决的话,具体实现思路是:我们需要不断地按照题目要求计算,直到得到 1 或者进入循环。具体来说,我们可以编写一个计算平方和的函数 squareSum,然后在一个 while 循环中不断调用这个函数,直到得到 1 或者进入循环。在每一轮计算中,我们将当前数字赋值给 n,然后调用 squareSum 计算出一个新的数字 m。如果 m 等于 1,说明这个数是快乐数;否则,我们继续按照题目要求计算,直到得到 1 或者进入循环。
def squareSum(n: int) -> int:
"""计算一个数每个位置上的数字的平方和"""
res = 0
while n > 0:
digit = n % 10
res += digit * digit
n //= 10
return res
def isHappy(n: int) -> bool:
seen = set() # 用来保存已经出现过的数字
while n != 1 and n not in seen:
seen.add(n)
n = squareSum(n)
return n == 1
在上面代码中,我们首先定义了一个计算平方和的函数 squareSum,这个函数会计算一个数每个位置上的数字的平方和。然后,我们使用一个 while 循环来按照题目要求进行计算,直到得到 1 或者进入循环。在每一轮计算中,我们首先将当前数字 n 加入到 seen 中,然后调用 squareSum 计算出一个新的数字 m,并将 m 赋值给 n。如果 n 已经出现在 seen 中了,那么说明我们进入了一个循环,可以直接退出循环。最后,我们判断 n 是否等于 1,如果是,返回 True,否则返回 False。
使用暴力枚举法虽然简单,但是时间复杂度较高,无法通过力扣的所有测试用例。因此,我们更推荐使用哈希表法来解决这个问题。
4、两数之和
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
**进阶:**你可以想出一个时间复杂度小于 O(n2)的算法吗?
- 定义一个哈希表
hash_map,用来记录每个数的下标。 - 遍历数组
nums,对于每个数num,计算出需要的另一个数target - num,并在哈希表中查找是否存在这个数。 - 如果存在,则直接返回这两个数的下标。
- 如果不存在,则将当前数的下标和值加入哈希表中,继续遍历数组。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
# 定义一个哈希表,用来记录每个数的下标
hash_map = {}
# 遍历数组 nums,对于每个数 num,计算出需要的另一个数 target - num,并在哈希表中查找是否存在这个数
for i, num in enumerate(nums):
complement = target - num
if complement in hash_map:
# 如果存在,则直接返回这两个数的下标
return [hash_map[complement], i]
else:
# 如果不存在,则将当前数的下标和值加入哈希表中,继续遍历数组
hash_map[num] = i
# 如果遍历完数组都没有找到满足条件的数,说明输入数据有误,返回空列表
return []
在解决这个问题时,我们首先要考虑如何遍历数组,并对于每个数计算出需要的另一个数。然后,我们可以使用哈希表来记录每个数的下标,这样在查找另一个数时可以快速地定位。最后,我们需要考虑一些特殊情况,比如输入数据为空或者没有满足条件的数。
如果我们使用暴力枚举法解决的话,我们需要对于每个数,依次遍历剩下的数,查找是否存在满足条件的数。
具体思路如下:
- 遍历数组
nums,对于每个数num1,依次遍历剩下的数num2。 - 如果找到两个数的和等于目标值
target,则返回它们的下标。 - 如果遍历完整个数组都没有找到满足条件的数,说明输入数据有误,返回空列表。
具体实现代码是:
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
# 遍历数组 nums,对于每个数 num1,依次遍历剩下的数 num2
for i, num1 in enumerate(nums):
for j, num2 in enumerate(nums[i+1:]):
j += i + 1 # 由于 j 是相对于 i 的偏移量,所以需要加上 i+1
# 如果找到两个数的和等于目标值 target,返回它们的下标
if num1 + num2 == target:
return [i, j]
# 如果遍历完整个数组都没有找到满足条件的数,说明输入数据有误,返回空列表
return []
需要注意的是,在这个算法中,我们需要对于每个数依次遍历剩下的数,时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组的长度。因此,如果输入数据很大,这个算法可能会超时。而使用哈希表的方法可以将时间复杂度降低到 O ( n ) O(n) O(n)。
B站上面卡尔老师对于这道题的解题思路是使用第一种详细的哈希表法解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1aT41177mK/?spm_id_from=333.788&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
5、四数相加Ⅱ
- 0 <= i, j, k, l < n
- nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
示例1:
输入:nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出:2
解释:
两个元组如下:
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0
示例2:
输入:nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出:1
提示:
n == nums1.length
n == nums2.length
n == nums3.length
n == nums4.length
1 <= n <= 200
-228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228
除了上述方法之外我们还可以使用Python 内置的 **defaultdict来解决这个问defaultdic**是一个类似于字典(dictionary)的容器类型,它是 Python 标准库 collections 中的一种数据类型,支持所有字典所支持的操作,但是在键不存在时,返回一个默认值(可以自己设定),而不是抛出 KeyError 异常。
这道题不推荐使用暴力,因为这样时间复杂度很高是通过不了的。
class Solution:
def fourSumCount(self, nums1, nums2, nums3, nums4):
dict = {}
for i in nums1:
for j in nums2:
if i+j in dict:
dict[i+j] += 1
else:
dict[i+j] = 1
count = 0
for i in nums3:
for j in nums4:
if -(i+j) in dict:
count += dict[-(i+j)]
return count
时间复杂度为 O ( n 2 ) O(n^2) O(n2),其中 n n n 是数组的长度。虽然使用了哈希表来优化查找过程,但仍然需要对数组进行遍历。如果输入数据很大,这个算法可能会超时。
使用Python内置函数解决:
from collections import defaultdict
class Solution:
def fourSumCount(self, nums1, nums2, nums3, nums4):
count_dict = defaultdict(int)
for i in nums1:
for j in nums2:
count_dict[i + j] += 1
count = 0
for i in nums3:
for j in nums4:
count += count_dict[-(i + j)]
return count
上述代码具体实现步骤如下:
- 使用 defaultdict(int) 来创建一个默认值为 0 的字典 count_dict,用于存储 nums1 和 nums2 中元素的和出现的次数。
- 遍历 nums1 和 nums2,将它们的和作为字典 count_dict 的键,值加 1。
- 遍历 nums3 和 nums4,计算它们的和的相反数,并在字典 count_dict 中查找对应的值,将值累加到计数器 count 中。
- 返回计数器 count 的值。
这种实现方式也是时间复杂度为 O ( n 2 ) O(n^2) O(n2) 的,其中 n n n 是数组的长度。
B站上面卡尔老师对于这道题的解题思路是使用第一种哈希表法解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1Md4y1Q7Yh/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
6、三数之和
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
首先我们来思考分析题目问题有哪些解决方法,大概就是下面这几种:
- 首先,可以考虑暴力解法。暴力解法的思路是枚举所有的三元组,时间复杂度为 O ( n 3 ) O(n^3) O(n3),不太可取。
- 考虑优化暴力解法。可以使用双指针的方法,将时间复杂度降为 O ( n 2 ) O(n^2) O(n2)。
- 进一步优化。可以先对数组进行排序,然后再使用双指针的方法,时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( l o g n ) O(log n) O(logn)。
- 可以使用哈希表的方法,时间复杂度为 O ( n 2 ) O(n^2) O(n2),空间复杂度为 O ( n ) O(n) O(n)。
由我们的分析可以看出来最优解法为第三种方法,即先对数组进行排序,再使用双指针的方法。
使用双指针的思路大致为:
- 对 nums 数组进行排序,排序后从小到大依次枚举每个数作为 a,同时设定两个指针 l 和 r 分别指向 a 的后面和数组末尾,即 l = a + 1,r = n - 1。
- 在 l 和 r 的指针范围内,判断 b + c 的值与 -a 的大小关系,如果 b + c > -a,则将指针 r 向左移动;如果 b + c < -a,则将指针 l 向右移动;如果 b + c = -a,则找到了一组解,将其加入结果列表中。
- 对于每个枚举到的数 a,如果它和它前面的数相等,就跳过这个数,避免重复计算。
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort() # 对数组进行排序
n = len(nums)
ans = []
for i in range(n):
if i > 0 and nums[i] == nums[i - 1]: # 跳过重复的数
continue
l, r = i + 1, n - 1 # 双指针初始值
while l < r:
if nums[l] + nums[r] + nums[i] == 0: # 找到一组符合条件的数
ans.append([nums[i], nums[l], nums[r]]) # 添加到结果集中
while l < r and nums[l] == nums[l + 1]: # 跳过重复的数
l += 1
while l < r and nums[r] == nums[r - 1]: # 跳过重复的数
r -= 1
l += 1 # 左指针右移
r -= 1 # 右指针左移
elif nums[l] + nums[r] + nums[i] < 0: # 三数之和小于0
l += 1 # 左指针右移
else: # 三数之和大于0
r -= 1 # 右指针左移
return ans # 返回结果
上述代码的详细实现步骤如下:
- 首先对数组进行排序,方便后续处理;
- 遍历数组中的每个数作为三元组中的第一个数;
- 对于每个三元组中的第一个数,使用双指针来找到剩余两个数;
- 在双指针中,l 指向当前三元组中的第二个数,r 指向当前三元组中的第三个数;
- 当三个数的和等于0时,即找到了一个符合要求的三元组,将其添加到答案数组中,并分别将 l 和 r 向中间移动一位,跳过重复的数;
- 当三个数的和小于0时,将 l 向右移动一位,尝试增大当前三元组的和;
- 当三个数的和大于0时,将 r 向左移动一位,尝试减小当前三元组的和;
- 最后返回答案数组。
除了双指针算法之外,还有一些其他的解决方法,如哈希表、暴力枚举等。但是,在时间复杂度和空间复杂度方面,双指针算法是效率最高的解决方法。
下面我给出暴力枚举法和哈希表法供大家学习参考。
暴力枚举法:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
ans = []
# 枚举三个数的组合
for i in range(n):
for j in range(i+1, n):
for k in range(j+1, n):
if nums[i] + nums[j] + nums[k] == 0:
ans.append([nums[i], nums[j], nums[k]])
ans = [list(t) for t in set(tuple(lst) for lst in ans)] # 去重
return ans
这种方法的时间复杂度较高,不适合处理较大的数据集,但对于小数据集可以得到正确的结果。
哈希表法:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
ans = []
hash_table = {}
for i in range(n):
hash_table[nums[i]] = i
for i in range(n):
for j in range(i+1, n):
if -nums[i]-nums[j] in hash_table and hash_table[-nums[i]-nums[j]] > j:
ans.append([nums[i], nums[j], -nums[i]-nums[j]])
ans = [list(t) for t in set(tuple(lst) for lst in ans)] # 去重
return ans
更推荐大家去使用双指针法来解决这个问题。
B站上面卡尔老师对于这道题的解题思路是使用第一种的双指针法解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1GW4y127qo/?spm_id_from=333.788&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
7、四数之和
- 0 <= a, b, c, d < n
- a、b、c 和 d 互不相同
- nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序返回答案 。
示例1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]
提示:
1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109
暴力枚举法我们可以使用四重循环来枚举四个元素,这种方法的时间复杂度为 O ( n 4 ) O(n^4) O(n4),不太可取。
这里我们只讲一下其中的双指针法和哈希表。
其中双指针法具体思路和代码实现可以参考第 15 题 三数之和 的解题思路,先对数组进行排序,然后在数组中枚举第一个数,在剩下的数中使用双指针的方法寻找满足条件的另外两个数,使得三个数的和等于 target。在寻找的过程中,为了避免重复的解,需要加入一些特判和判断。
然后哈希表法是先将数组 nums 中的两个元素相加,将它们的和作为哈希表的键,它们的下标作为哈希表的值。接下来,遍历数组 nums 中的另外两个元素,如果它们的和等于 target 减去哈希表中的键,就说明找到了符合要求的四元组。
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
n = len(nums)
if n < 4: # 数组长度小于 4 时,直接返回空列表
return []
nums.sort() # 对数组进行排序
res = [] # 存储结果的列表
for i in range(n-3): # 枚举第一个数
if i > 0 and nums[i] == nums[i-1]: # 跳过重复的数
continue
if nums[i] + nums[i+1] + nums[i+2] + nums[i+3] > target: # 如果当前的最小值都大于 target,则结束
break
if nums[i] + nums[n-3] + nums[n-2] + nums[n-1] < target: # 如果当前的最大值都小于 target,则跳过
continue
for j in range(i+1, n-2): # 枚举第二个数
if j > i+1 and nums[j] == nums[j-1]: # 跳过重复的数
continue
if nums[i] + nums[j] + nums[j+1] + nums[j+2] > target: # 如果当前的最小值都大于 target,则结束
break
if nums[i] + nums[j] + nums[n-2] + nums[n-1] < target: # 如果当前的最大值都小于 target,则跳过
continue
left, right = j+1, n-1 # 双指针初始值
while left < right: # 双指针遍历
temp_sum = nums[i] + nums[j] + nums[left] + nums[right] # 计算当前四数之和
if temp_sum == target: # 如果等于 target,则加入结果,并跳过重复的数
res.append([nums[i], nums[j], nums[left], nums[right]])
while left < right and nums[left] == nums[left+1]:
left += 1
while left < right and nums[right] == nums[right-1]:
right -= 1
left += 1
right -= 1
elif temp_sum < target: # 如果小于 target,则左指针右移
left += 1
else: # 如果大于 target,则右指针左移
right -= 1
return res # 返回结果列表
在上述代码中,我们首先对数组进行排序,然后依次枚举前两个数的下标 i 和 j。在每次枚举中,我们通过双指针的方式,从剩下的数中找到另外两个数,使得四数之和等于目标值 target。在这个过程中,需要注意以下几点:
- 为了避免重复,我们需要对每一个枚举到的数都跳过所有与之前枚举到的数相同的情况。
- 当四数之和小于目标值时,需要将左指针右移一位,以使得和变大;当四数之和大于目标值时,需要将右指针左移一位,以使得和变小。
- 对于重复的数,我们只需将指针移动到第一个不同的数处即可。
最终,我们可以得到所有不重复的四元组,使得它们的和等于目标值 target。
使用哈希表解决:
class Solution(object):
def fourSum(self, nums, target):
# 创建一个哈希表,记录每个数字出现的次数。
hashmap = dict()
for n in nums:
if n in hashmap:
hashmap[n] += 1
else:
hashmap[n] = 1
# 创建一个空的集合,用于存储结果。
ans = set()
# 使用三重循环枚举三个数(i,j,k),其中i<j<k。
for i in range(len(nums)):
for j in range(i + 1, len(nums)):
for k in range(j + 1, len(nums)):
# 计算目标值与三个数之和的差值,判断该差值是否在哈希表中存在。
val = target - (nums[i] + nums[j] + nums[k])
if val in hashmap:
# 计算差值在三个数中出现的次数,如果大于等于当前哈希表中该差值的出现次数,则将四个数进行排序,并添加到集合中。
count = (nums[i] == val) + (nums[j] == val) + (nums[k] == val)
if hashmap[val] > count:
ans_tmp = tuple(sorted([nums[i], nums[j], nums[k], val]))
ans.add(ans_tmp)
else:
continue
# 返回集合的列表形式作为最终结果。
return list(ans)
B站上面卡尔老师对于这道题的解题思路是使用第一种的双指针法解决,讲得很不错,在这里推荐大家去看看他的教学视频:
https://www.bilibili.com/video/BV1DS4y147US/?spm_id_from=333.788&vd_source=eae0406d86828f39f6ac3a3b0e8a2a34
四、如何选择哈希表实现对象?
在上面的题目中,我们在定义选择哈希表的实现对象的时候是不一样的,有些朋友可能就会好奇我们什么时候选择数组作为哈希表更好,什么时候选择set作为哈希表更好,什么时候选择map作为哈希表更好?
下面我来做一个总结,仅供参考:
- 数组作为哈希表
如果题目中明确说明了数据的范围,可以直接利用数组实现哈希表。例如,当题目要求哈希表中的键(即数组中的元素)取值范围为[0, 100]时,可以定义长度为101的数组作为哈希表,键值为i的元素就存放在下标为i的位置上。这种方法的时间复杂度为O(1),是最快的,但需要额外的空间来存储数组。 - set作为哈希表
如果不需要对哈希表中的键进行计数,而只是需要判断某个元素是否存在于哈希表中,可以使用set作为哈希表。这种方法的时间复杂度为O(1),比使用数组作为哈希表更节省空间。 - map作为哈希表
如果需要对哈希表中的键进行计数,可以使用map作为哈希表。map可以实现键值对的映射,并记录每个键在哈希表中出现的次数。这种方法的时间复杂度为O(1),但空间开销较大。
在实际应用中,我们需要根据题目的要求来选择适合的哈希表实现对象。具体而言,当哈希表中的键取值范围不大,且需要对键进行计数时,可以选择数组或map作为哈希表;当哈希表中的键取值范围较大,且只需要判断键是否存在时,可以选择set作为哈希表。
表格总结如下:
| 哈希表实现对象 | 适用场景 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|
| 数组 | 键取值范围小,需要对键进行计数 | O(1) | 额外空间 |
| set | 键取值范围大,只需判断键是否存在 | O(1) | 额外空间 |
| map | 键取值范围小或大,需要对键进行计数,且不需要自定义哈希函数 | O(1) | 额外空间 |