第一题 AcWing 4864. 多边形

一、题目

1、原题链接

4864. 多边形

2、题目描述

如果一个正多边形的边数 n 能被 4 整除，那么就称该正多边形是美丽的。

现在，给定一个正多边形的边数 n，请你判断它是否是美丽的。

输入格式

第一行包含整数 T，表示共有 T 组测试数据。

每组数据占一行，包含一个整数 n。

输出格式

每组数据输出一行结果，如果给定正多边形是美丽的，则输出 YES，否则输出 NO。

数据范围

前 3 个测试点满足 1≤T≤10。
所有测试点满足 1≤T≤10⁴，3≤n≤10⁹。

输入样例：

4
3
4
12
1000000000

输出样例：

NO
YES
YES
YES

二、解题报告

1、思路分析

（1）按照题意模拟即可，输出答案即为所求。
（2）注意YES与NO的大小写问题。

2、时间复杂度

时间复杂度为O(n)

3、代码详解

#include <iostream>
using namespace std;
int t;
int main(){
    cin>>t;
    while(t--){
    	int n;
    	cin>>n;
    	if(n%4==0) cout<<"YES"<<endl;
		else cout<<"NO"<<endl; 
	}
    return 0;
}

第二题 AcWing 4865. 有效类型

一、题目

1、原题链接

4865. 有效类型

2、题目描述

在本题中，关于有效类型字符串，具体定义如下：

• int 是有效类型字符串。
• 如果字符串 X 和字符串 Y 都是有效类型字符串，则 pair<X,Y> 是有效类型字符串。 现有一行若干个单词，每个单词要么是 pair，要么是 int，并且其中 int 的数量恰好为 n 个。

你可以在不改变单词顺序的前提下，在这一行中任意添加 <、>、, 符号。

你的任务是 构造出一个有效类型字符串。

输出这个有效类型字符串。

注意：

有效类型字符串中不含空格或其它多余字符。 可以证明如果存在满足条件的有效类型字符串，那么它一定是唯一的。
如果不存在满足条件的有效类型字符串，输出 Error occurred即可。

输入格式

第一行包含整数 n，表示给定单词中 int 的数量。

第二行包含若干个单词，每个单词要么是 pair，要么是 int。

输出格式

输出满足条件的有效类型字符串，如果不存在，则输出 Error occurred。

注意，有效类型字符串中不含空格或其它多余字符。

数据范围
前 6 个测试点满足：1≤n≤5。
所有测试点满足：1≤n≤10⁵，输入的总单词数量不超过 10⁵，输入的 int 数量恰好为 n。

输入样例1：

3
pair pair int int int

输出样例1：

pair<pair<int,int>,int>

输入样例2：

1
pair int

输出样例2：

Error occurred

二、解题报告

1、思路分析

思路来源：y总讲解视频
y总：yyds

数据范围为10⁵，时间复杂度控制在O(nlogn)
（1）可以发现每一个满足条件的有效类型字符串，都满足一个以pair为根结点int为左右儿子的二叉树。而且，每出现一个pair，必须有左右儿子；每出现一个int，必须没有左右儿子（即输入多组int是不合法的）。所以，只有满足每个根结点pair都有孩子，每个int都没有孩子，而且构造成的二叉树正好将所有的输入都用到（即不能多单词也不能少单词），就是满足条件类型的字符串。否则就不是有效类型字符串。而输入和输出便是二叉树的前序遍历。

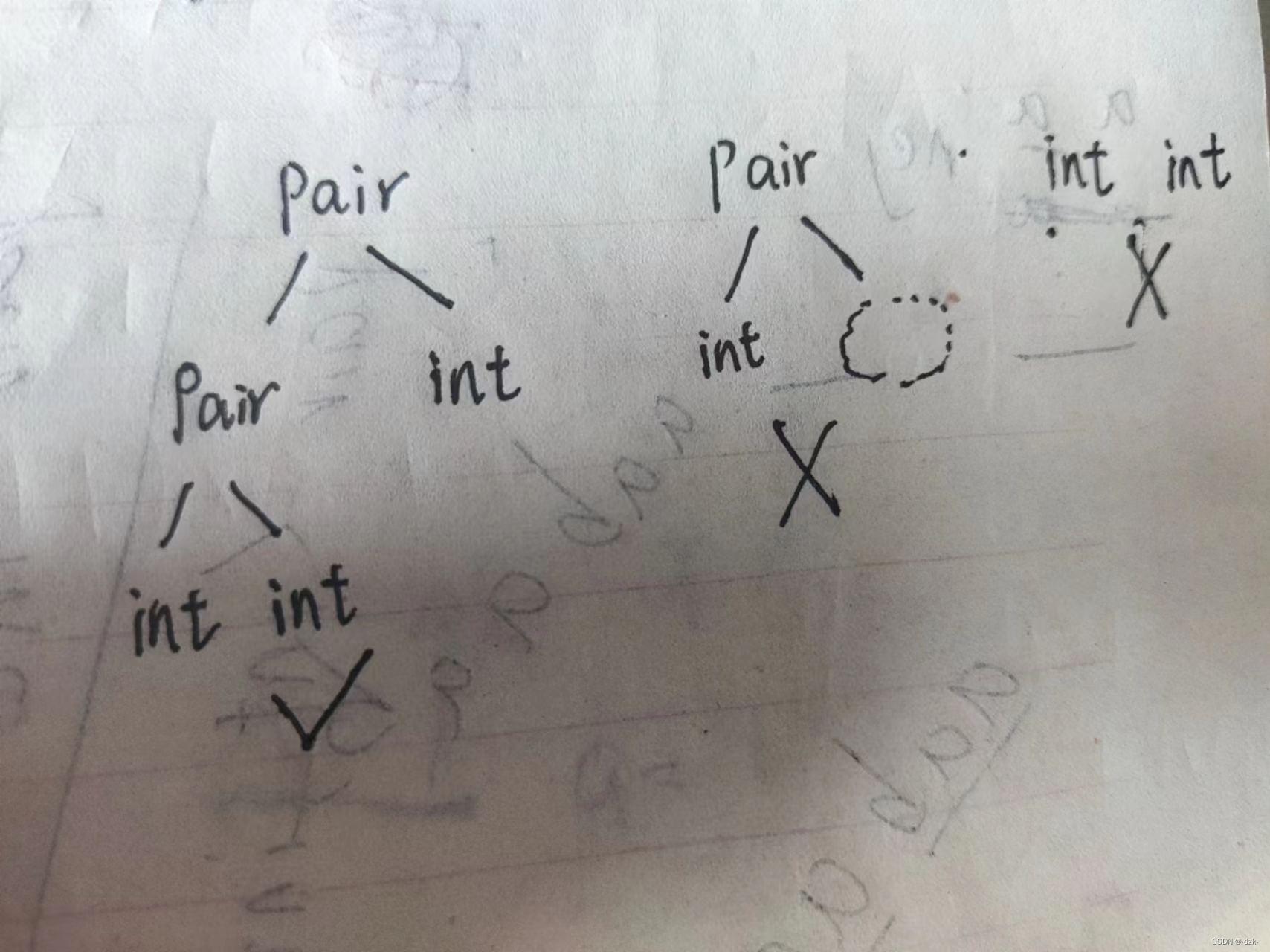
（2）我们可以通过上述规则，来判断给定的输入能否构造出上述的二叉树，如果可以，我们对二叉树的前序遍历进行输出（同时，每输出一个根结点pair，之后输出一个<，在遍历完左子树后输出一个,，遍历完右子树后输出一个>）。
（3）模拟上述过程，输出即为所求。

2、时间复杂度

时间复杂度为O(n)

3、代码详解

#include <iostream>
#include <string>
using namespace std;
string s,ans;
bool dfs(){
	if(cin>>s){              //每次调用dfs建树时，必须有输入，如果调用了但是没有输入，直接返回false
		if(s=="pair"){       //如果输入pair需要递归建立左右子树
			ans+=s+'<';
			if(!dfs()) return false;  //递归构建左子树
			ans+=',';
			if(!dfs()) return false;  //递归构建右子树
			ans+='>';
		}
		else ans+=s;        //如果输入int直接加到答案中即可
	}
	else return false;
	return true;
}
int main(){
	int n;
	cin>>n;
	bool flag=dfs();
	string tmp;
	if(!flag||cin>>tmp) cout<<"Error occurred";   //如果无法构成树（缺少输入或者输入出现多余），则不合法
	else cout<<ans;     //正好用到所有输入的单词，而且可以按照规则构造成二叉树，按题目要求输出答案
    return 0;
}

第三题 AcWing 4866. 最大数量

一、题目

1、原题链接

4866. 最大数量

2、题目描述

一个无向图有 n 个点，编号 1∼n。

这些点之间没有任何边。

给定 d 个需求，编号 1∼d。

其中，第 i 个需求是让点 xi 和点 yi 连通。

需求可能存在重复。

在本题中，你需要依次解决 d 个问题，编号 1∼d。

其中，第 i 个问题是，请你在图中添加恰好 i 条无向边（不能添加重边和自环），使得：

1. 前 i 个需求都得到满足。
2. 所有点的度的最大值尽可能大。

对于每个问题，你不需要输出具体方案，你只需要 输出度的最大可能值。

注意：

如果点 a 和点 b 之间存在路径，则称点 a 和点 b 连通。 图中与点 a 关联的边数，称为点 a 的度。 d
个问题之间是相互独立的，每个问题的答案都必须独立计算。

输入格式

第一行包含两个整数 n,d。

接下来 d 行，其中第 i 行包含两个整数 xi,yi，表示第 i 个需求是让点 xi 和点 yi 连通。

输出格式

共 d 行，其中第 i 行输出第 i 个问题中，度的最大可能值。

数据范围

前三个测试点满足，2≤n≤10。
所有测试点满足，2≤n≤1000，1≤d≤n−1，1≤xi,yi≤n，xi≠yi。

输入样例1：

7 6
1 2
3 4
2 4
7 6
6 5
1 7

输出样例1：

1
1
3
3
3
6

输入样例2：

10 8
1 2
2 3
3 4
1 4
6 7
8 9
8 10
1 4

输出样例2：

1
2
3
4
5
5
6
8

二、解题报告

1、思路分析

思路来源：4866. 最大数量
y总yyds

数据范围为1000，时间复杂度控制在O(n²)或O(n²logn)
（1）针对每个需求i让点xi和yi连通，即使xi和yi在一个集合中，也就是用到了并查集的合并操作。
（2）前i个操作总共可以使用i条边使每个点相连，而我们满足前i个需求，即让xi和yi连通，可能不会用完i条边。假设我们已经满足前i个需求后还剩余cnt条边，而前i个需求已经将所有元素合并成了某些集合（k1，k2，k3，...，kd），而这些集合中点度数最大为集合中元素数-1，即其中的某个点与其他所有点都相连。我们将剩余的边数连到某个集合中，不会改变该集合的最大度数。如果用边将两个集合相连，则合并后集合的度比合并前任意一个集合的度都要大（合并后集合的度也就是合并后集合的总元素数-1）。而总共可以合并cnt+1个集合，所以我们需要将元素数量最多的前cnt+1个集合合并，这样可以保证使用cnt条边后，合并完的集合度是比其他任何情况都要大。
（3）按照上述过程模拟，计算出前cnt+1个集合的总点数sum，则最大度为sum-1，输出答案即为所求。

2、时间复杂度

时间复杂度为O(n²logn)

3、代码详解

#include <iostream>
#include <algorithm>
using namespace std;
const int N=1010;
int p[N],num[N],nums[N];     //p[]存储每个结点的祖宗结点，num[]存储集合大小，nums[]存储集合合并后每个合并后集合的点数
//并查集查找祖宗结点
int find(int x){
    if(p[x]!=x) p[x]=find(p[x]);
    return p[x];
}
//按降序排列cmp函数
bool cmp(int A,int B){
    return A>B;
}
int main(){
    int n,d;
    cin>>n>>d;
    //初始化并查集数组
    for(int i=1;i<=n;i++){
        p[i]=i;
        num[i]=1;
    }
    int cnt=0;        //cnt记录满足前i个需求后还剩余多少条边
    while(d--){
        int x,y;
        cin>>x>>y;
        if(find(x)!=find(y)){     //如果x、y不在一个集合中，则合并
            num[find(y)]+=num[find(x)];
            p[find(x)]=find(y);
        }
        else cnt++;       //如果x，y已经在一个集合中则无需操作，可以省下一条边可以使用
        int t=0;
        //将每个集合中点的数量记录在nums数组中
        for(int i=1;i<=n;i++){
            if(p[i]==i){
             nums[t++]=num[i];
            }
         }
        sort(nums,nums+t,cmp);     //降序排列nums数组
        int sum=0;      
        //取前cnt+1个点数最多的集合，将它们的点数记录在sum中
        for(int i=0;i<t&&i<cnt+1;i++){
            sum+=nums[i];
        }
        cout<<sum-1<<endl;      //sum-1即为所求
    }
    return 0;
}