RL笔记：动态规划(2): 策略迭代

news2024/9/23 13:16:41

0. 前言

(4.3) 策略迭代

Example 4.2: Jack’s Car Rental

Exercise 4.4

Exercise 4.5

Exercise 4.6

Exercise 4.7

0. 前言

Sutton-book第4章（动态规划）学习笔记。本文是关于其中4.2节（策略迭代）。

(4.3) 策略迭代

基于上节（RL笔记：动态规划(1): 策略估计和策略提升）的策略提升，一旦从策略\pi出发找到了一个更好的策略 $\pi'$ ；很显然，我们可以进一步基于 $\pi'$ 找到下一个更好的 $(\pi')'$ 。重复这一过程，就可以得到不断改进的策略，直到收敛到最优策略。这一过程称为策略迭代（Policy Iteration），如下图所示：

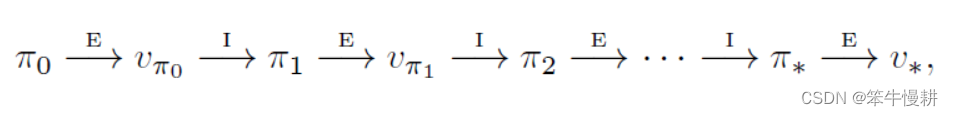
其中，“E”表示Evaluation，即上上节所述的策略评估；“I”表示Improvement，即上节所述的策略提升。由于每一步都必然可以得到一个更好的策略（除非已经到达最优策略，如上节所述），因此这一迭代过程最终必然收敛于最优策略（类似于数学分析中的单调有界序列必定收敛的命题）。

每一轮（each iteration）的策略评估是以是上一轮结束后得到的策略（policy）的值函数（value function）为初始值的。策略迭代的算法流程如下所示：

图1 基于状态值函数的策略迭代

Some points and tips：

这个两步策略是不是有点类似于机器学习中的EM（Expectation-Maximization算法）的套路？
第2步的策略评估中并没有像4.1节中的策略评估那样对动作进行求和： $\sum\limits_a \pi(a|s)$ 。这是因为在这个迭代算法中第3步的策略提升采用的是贪婪算法，总是采取动作值函数最大的动作，所得到的策略是确定性策略（deterministic policy），每个状态与动作是一一对应的，所以由于 $\sum\limits_a \pi(a|s) = \pi(a_{max}|s)=1$ ，可以进行简化。
第2步的策略评估中同时计算前后两轮迭代的各对应状态的值函数的变化量并得到变化量绝对值的最大值Δ，这个是用于收敛判断以及early-stop。如果满足条件 $\Delta < \theta$ ，即判定近似收敛并退出迭代过程

策略评估时根据当前策略 $\pi$ 选择动作，策略提升时根据基于策略 $\pi$ 计算所得的值函数并基于 $\max\limits_a Q(s,a)$ 准则选择动作。除非当前策略 $\pi$ 已经是最优策略，否则必然得到比当前策略 $\pi$ 更好的策略。所以这一迭代过程最终必定“近似地”收敛于最优策略（近似是由于采用了early-stop控制）。

Example 4.2: Jack’s Car Rental

Jack负责管理一个全国性租车公司的两个站点。有顾客来租车时，如果有车可租则将车租出并收入10美元（是指每天10美元吗？还是说每借一次就是10美元不论天数？）；如果无车可租则失去一笔生意。车归还后的次日车子可以重新出租。为了尽量确保两个站点都有车可租，Jack会在晚上在两个站点之间移动车辆，每辆车移动耗费2美元。每个站点每天来租车和来还车的人数均服从泊松分布： $Prob(n) = \frac{\lambda^n}{n!} e^{-\lambda}$ , $\lambda$ 为数学期望。假定站点1的租车人数和还车人数的数学期望分别为3和4，站点2的租车人数和还车人数的数学期望分别为3和2。为了简化问题，进一步假定每个站点车辆不能超过20辆，超过这个数量的车被归还给租车公司。每个晚上可以在两个租车点移动的车最多5辆。考虑折扣系数 $\gamma = 0.9$ ，并且作为一个continuing finite MDP问题处理：以每天作为一个time step; 状态代表每天结束时留在各站点的存车数。

状态用state = {num1: 站点1保有车数；num2: 站点2保有车数}，这个保有车数是指每天最终（在两个站点挪动车之后）各站点保有车数。每天车的数量变化取决于以下因素：

当天借出车数：遵循泊松分布，以及当前站点存车状况
当天还入车数：遵循泊松分布，以及当前站点存车状况
当晚挪出或者挪入车数：是取决于agent（本问题中就是指Jack）基于policy所采取的行动

代码实现例可以参考：

https://github.com/ShangtongZhang/reinforcement-learning-an-introduction/chapter04/car_rental.py

其中expected_returns()函数实现的就是

这个例子中有一个明显的不太合理的地方，就是一辆车借出后的租金固定为10美元，与租用天数无关。这样可能是为了方便问题简化处理吧。如果修改为一辆车借出去每天租金10美元的话，情况会怎么样呢？

Exercise 4.4

前面所示的策略迭代算法有一个细微的bug。当存在两个或多个同样好的策略（所谓同样好是指啥？），它会导致在这些同样好的策略之间来回切换因而永远停不下来。请修改以上伪代码使得能够确保在有限次迭代后收敛和退出。

【ans】

在第3步中有一个收敛判决：if old_action 不等于 $\pi(s)$ ...

如果在当前策略\pi中，在状态s时有多个动作同样好（equally good），此时 $\pi(s)$ 不是一个值，而是包含多个元素的集合，以上判决处理将会导致问题。有两种解决方案：

其一：将以上收敛判决改为 $if \ old\_action \notin \pi(s):$ ...

其二：追加tie-breaking rule between equally good actions，使得在存在多个同样好的动作时，策略 $\pi(s)$ 总能产生唯一确定性的动作

Exercise 4.5

试给出与以上面向状态值函数的策略迭代算法类似的面向动作值函数的策略迭代算法。

图2 基于动作值函数的策略迭代

以上解答摘自LyWangPX/Reinforcement-Learning-2nd-Edition-by-Sutton-Exercise-Solutions(github.com)

变更点仅仅是第2步的策略评估中将基于“状态值函数的贝尔曼方程”的迭代更新改为基于“动作值函数的贝尔曼方程”的迭代更新。进一步由于第3步中是基于贪婪方法进行策略提升，所得的是确定性的策略，因此Q(s,a)的更新方程可以进一步简化（理由同上面关于基于状态值函数的策略迭代的解说）为(去掉对a’的求和)：

$Q(s,a) \leftarrow \sum\limits_{s',r}p(s',r|s,a)[r + \gamma Q(s',\pi(s'))]$

第3步中 $\pi(s)$ 的更新看似写法不同，其实没有本质变化。因为(之所以成立仍然是因为贪婪决策):

$Q(s,a) = \sum\limits_{s',r}p(s',r|s,a)[r + \gamma Q(s',\pi(s'))] = \sum\limits_{s',r}p(s',r|s,a)[r + \gamma V(s')]$

，前面的基于状态值函数的策略迭代流程中其实本质上也是基于动作值函数的贪婪决策。

Exercise 4.6

假定只能考虑软策略（soft policy），即在每个状态下选择各个动作的概率不得低于 $\frac{\epsilon}{\mathcal{A}(s)}$ . 试修改上述的策略迭代算法以对应这种要求。

【Ans】

相比图1所示基于硬策略（hard policy, i.e, greedy policy）原始的策略迭代流程，需要做以下两点修改：

在策略评估（policy evaluation）中，由于软策略中每个状态下对应的动作不是唯一的，对状态值函数的估计需要对动作进行求和，即恢复为标准的状态值贝尔曼方程
在策略提升（policy improvement）中，要将更新后的策略修改为软策略，即：取导致动作价值最大的动作作为软策略的greedy-action，其余则作为epsilon-action。然后，同样是基于greedy-action进行收敛判决。