来源：投稿 作者：kon
编辑：学姐

前言

众所周知，火热的对比学习不仅在CV取得了很多成果，也在NLP、推荐等领域大放异彩。自然的，有人将对比学习引入了图表示学习领域，利用图本身的结构与结点自身的特征进行对比学习，实现了端到端的结点性质预测。

今天为大家带来的就是图表示学习领域里对比学习的开山之作，「《Deep Graph Infomax》」提出的经典架构DGI。DGI通过对Deep Info Max理论的再推导，提出了无监督学习范式Deep Graph Infomax，在多个数据集上的表现甚至超过了有监督学习。

理论推导

定义X为某个结点的node embedding，s为某个图的Graph embedding。作者借鉴了CV领域中DGI的思想，进行了概率上的推导。

分类器越可以辨认出正确的样本对（X,s）代表着X和s的共现概率越高，我们当然希望summary vector和结点表示集合X共现概率更大，因为这意味着summary vector代表着集合X独有的特征，证明这个表示质量很高。因此，图对比学习问题可以转化为辨别正确样本对的问题。

「其中，边缘分布被采样到的概率推导式为」：

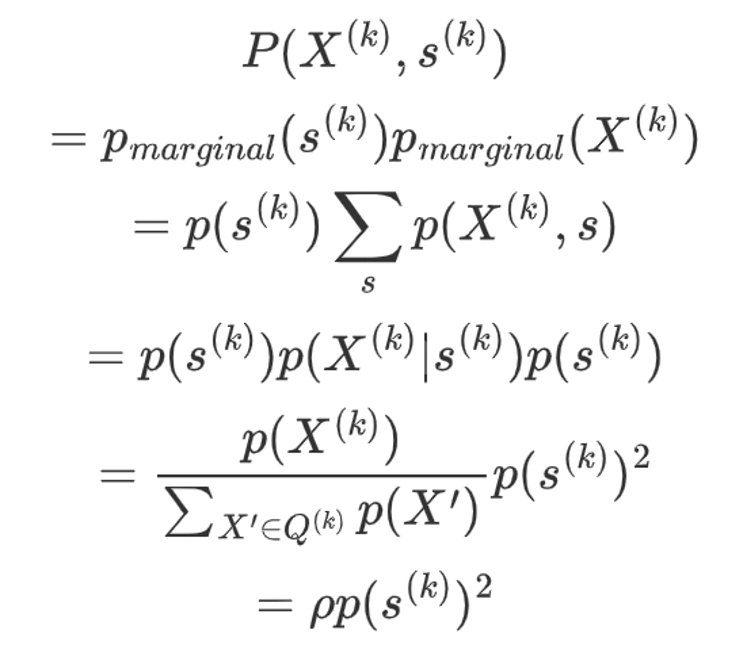
「联合分布被采样到的概率为」：

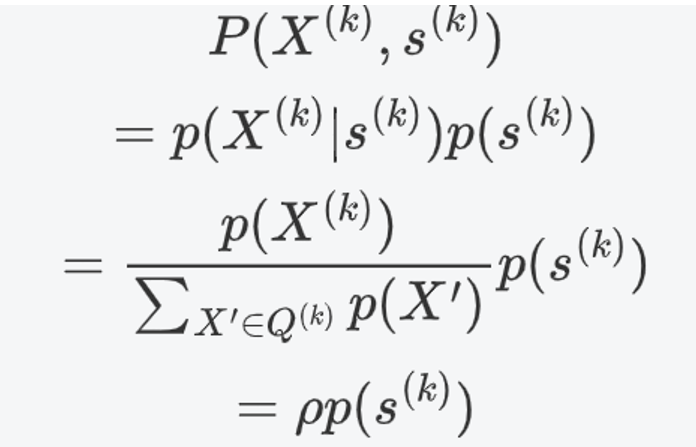
可以看到，样本对（X,s）在联合分布被采样到的概率比以边缘分布被采样到的概率要大。即，分类器分类一个样本来自联合分布的出错概率更小。

这符合直觉，因为仅当变量独立时，边缘分布乘积才为联合分布。现实中，变量之间几乎都有关联，所以用边缘分布乘积去估计不准确。在图表示学习中，这个理论可以理解为同一图的不同结点都或多或少有着关联，但不同图的结点之间是没有关联的。

进一步的，可以利用琴生不等式得到结论：最优分类器的分类错误率的范围在1/2|X|到1/2之间。这符合batch内样本越多、对比学习效果越好的经验。

推论1：

如果Readout函数是单射的，s包含状态比X的多，那么最优分类器会让的状态个数与X的状态个数一致。简单理解就是，s和X一一对应，对于不同的X都有唯一summary vector与之对应，提高embedding的质量。

定理1：

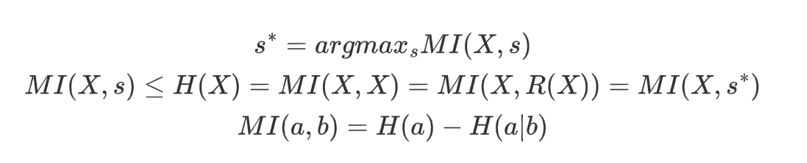
定理1表明，对于有限的输入集和合适的确定性函数，最优s意味着最大互信息，所以可以使用最小化鉴别器中的分类误差来最大化输入X和输出s之间的互信息。

推论2：

最小化联合分布采样以及边缘分布采样的分类错误相当于最大化MI（X，h），h为结点i聚合邻居后的表示。

模型

经过了复杂、严密的推导后，就可以很容易地理解本文提出的模型了！

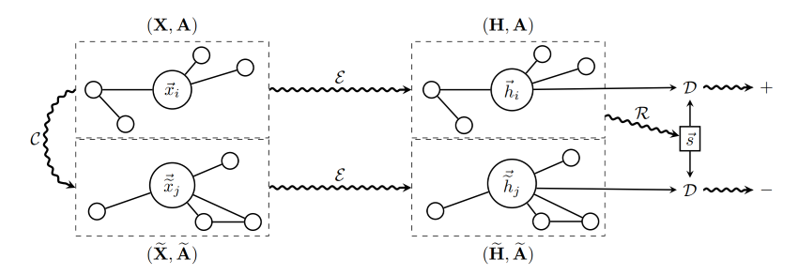
观察上图，分别将正样本与负样本送入同一网络，得到对应的patch representation，对正样本提取Global representation，作为summary vector分别与正、负样本进行对比学习。

「训练流程为：」

1.对正样本使用corruption function得到负样本实例

2.编码得到正、负样本的patch representation，就是结点的embedding集合

3.将正样本的patch representation送入Readout函数，得到正样本的图级别summary vector

4.将正、负样本的patch representation以及summary vector输入判别器，正样本输出为正，负样本输出负，通过梯度下降更新参数

试验部分

定义X为特征，A为邻接矩阵，Y为标签。

在直推式学习中，各数据集、各网络的分类准确率如下所示。可以看到，DGI在无监督的情况下一举超越了有监督学习的GCN。

「在直推式任务中，采用如下聚合、传播范式」：

在归纳式学习也有很好的表现，作者测试了Reddit数据集和PPI数据集，试验结果证明「DGI也超过了一些有监督学习方法」：

在大图上采用的GraphSage范式，即mean pooling：

针对reddit数据集，使用的聚合规则以及传播规则亦作了微调，但整体架构没有变化。

总结

「DGI」是一个node level的图表示学习架构，作者只在试验阶段只针对node classification做了一些工作，所以可以认为该架构只能训练出好的node embedding，至于graph embedding，作者把这些工作留给了后来人。

如果可以设计出一个优秀的Readout架构，DGI自然就可以做graph embedding了，不敢这一点需要整个科研界充分发挥想象力。不管怎么说，DGI为后来的图对比学习打下了坚实的基础，是一篇不可多得的好文章。

关注下方《学姐带你玩AI》🚀🚀🚀

回复“500”免费获取经典论文合集（包含CV、NLP各个细分方向）

码字不易，欢迎大家点赞评论收藏！