电子技术——A类输出阶

因为射极跟随器具有较低的输出阻抗，射极跟随器是A类输出阶的典型代表。我们之前已经学习过射极跟随器的小信号模型，本节我们讨论其大信号模型。

传输特性

下图展示了一个射极跟随器的原理图：

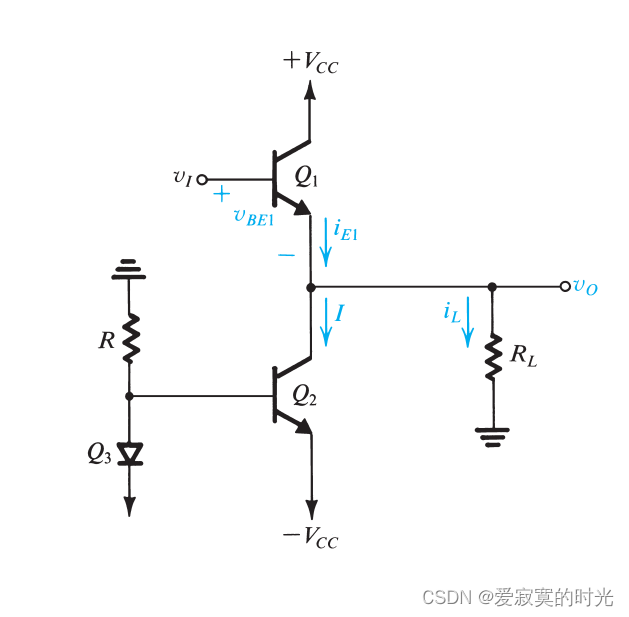
其中 $Q_1$ 为射极跟随器，电流源 $Q_2$ 提供偏置电流 $I$ 。传输方程为：

$$v_O=v_I-v_{BE1}$$

其中 $v_{BE1}$ 的大小依赖于 $i_{E1}$ 因为 $i_{E1}=I+i_L$ 因此依赖于输出电流 $i_L$ 若我们忽略输出电流的影响（假设一直是0.7V）那么传递曲线为：

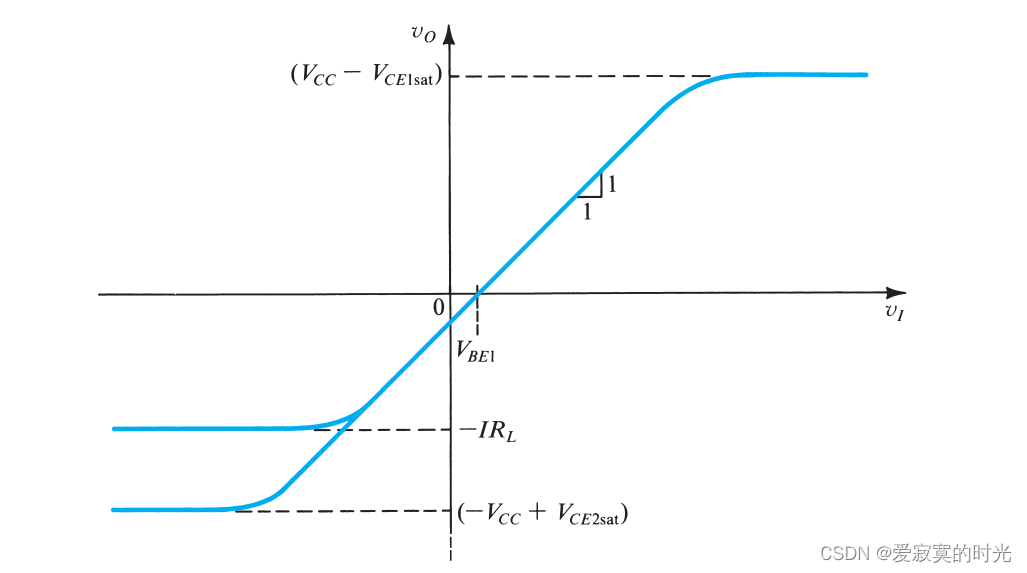
当 $Q_1$ 饱和时，达到输出最大电压：

$$v_{Omax}=V_{CC}-V_{CE1sat}$$

对于负向，当 $Q_2$ 饱和的时候，达到理论的最小输出电压：

$$V_{Omin}=-V_{CC}+V_{CE2sat}$$

或是 $Q_1$ 截止：

$$V_{Omin}=-I{R}_L$$

若想达到理论的最小输出电压，必须满足：

$$I\ge \frac{|-V_{CC}+V_{CE2sat}|}{R_L}$$

输出波形

还是考虑上面的电路，若忽略 $V_{CEsat}$ 并且偏置电流 $I$ 选择合适，那么波形就可以在$-V_{CC}$ 到 $+V_{CC}$ 摆动，静态点为零电压，如图：

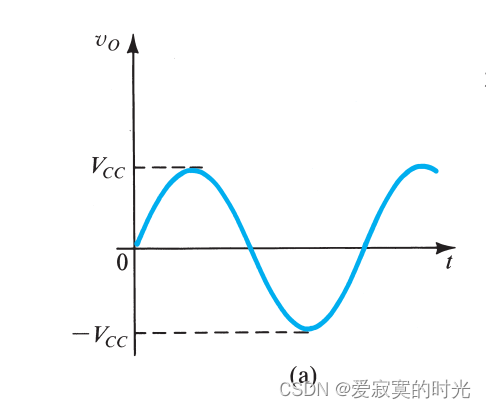
对应的 $v_{CE1}=V_{CC}-v_O$ 的波形对应如下：

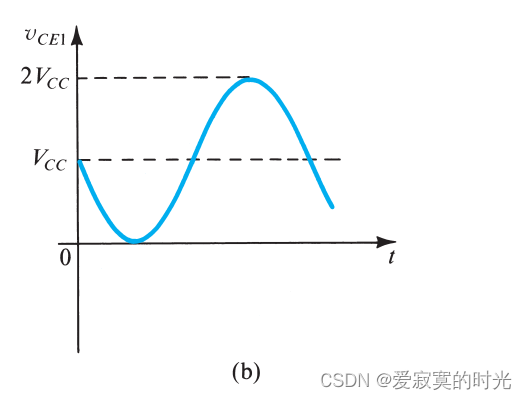
若假设 $Q_2$ 进入饱和区时 $Q_1$ 恰好关闭，即：

$$I=V_{CC}/R_L$$

则 $i_{C1}$ 电流为：

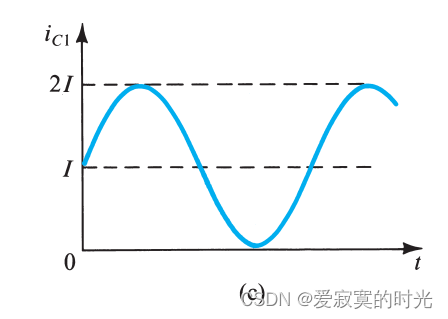
耗散功率

下图展示了 $Q_1$ 的 瞬时耗散功率 变化 $p_{D1}\equiv v_{CE1}{i}_{C1}$ ：

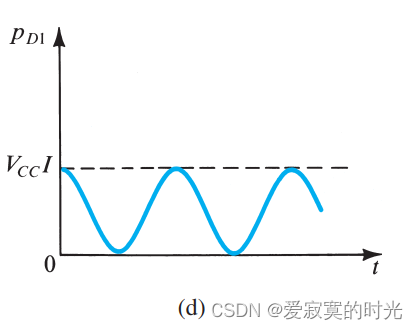
上图中我们发现最大瞬时耗散功率为 $V_{CC}I$ 此时 $Q_1$ 没有输入信号，也就是静态点。也就是说，当放大器没有信号输入的时候，此时静态管的功率耗散达到最大值，我们知道无信号输入很有可能发生并且发生的时间可能很长，因此 $Q_1$ 将可能持续保持在高功率的状态下。

其中 $Q_1$ 的耗散功率取决于负载 $R_L$ ，考虑一种极端情况，即负载开路的情况， $Q_1$ 通过的电流一直是 $I$ ，此时耗散功率取决于输出电压 $v_O$ ，最大功率 $p_{D1}=2V_{CC}I$ 发生在 $v_O=-V_{CC}$ 的时候。然而，这个情况不可能保持太久，因此在设计上不需要考虑这一点，而此时的平均功率为 $V_{CC}I$ 。另外一种极端情况发生在 $R_L=0$ 的时候，即负载短路。理论情况下 $R_L$ 和 $Q_1$ 会通过无限大的负载电流，实际情况下受到非线性因素的影响，此时 $Q_1$ 会达到最大耗散功率，此时BJT的结温可能会达到极限值，因此为了防止这种情况，输出阶应该配备 短路保护电路 。

电流源 $Q_2$ 的耗散功率也必须考虑在内，因为 $Q_2$ 通过的电流值不变始终是 $I$ 。因此 $Q_2$ 的最大功率为 $2V_{CC}I$ 此时 $v_O=V_{CC}$ ，同样这个情况不会发生太长时间，其平均功率为 $V_{CC}I$ 。

能量转换效率

输出阶的能量转换效率定义为：

$$\eta \equiv \frac{\text{Load power}(P_L)}{\text{Supply power}(P_S)}$$

对于输出一个峰值为 $\widehat{V_o}$ 正弦信号，则负载的平均功率为：

$$P_L=\frac{(\widehat{V_o}/\sqrt{2}{)}^2}{R_L}=\frac{1}{2}\frac{{\widehat{V_o}}^2}{R_L}$$

通过 $Q_1$ 和电源的平均电流为 $I$ 电源电压为 $2V_{CC}$ 因此电源的平均功率为：

$$P_S=2V_{CC}I$$

则能量转换效率为：

$$\eta =\frac{1}{4}\frac{{\widehat{V_o}}^2}{I{R}_L{V}_{CC}}=\frac{1}{4}(\frac{\widehat{V_o}}{I{R}_L})(\frac{\widehat{V_o}}{V_{CC}})$$

因为 $\widehat{V_o}\le V_{CC},\widehat{V_o}\le I{R}_L$ 因此当：

$$\widehat{V_o}=V_{CC}=I{R}_L$$

的时候达到理论能量转换效率最大值 $25\%$ 。因为其过低的能量转换效率，A类输出阶很少被使用在大功率（大于1W）的输出设备上。实际上的能量转换效率在 $10\%\sim 20\%$ 。