校验码

计算机在接收相应信息的时候能够识别的的都是一些电器信号，01二进制这种，在网络上传递信息的时候，也是通过电器信号、或者电流之类的来进行传递。电流在传输的过程当中，距离很长，一千公里、一万公里都有，那么长度很长的情况下，电流是否会产生衰竭呢？或者是一些不知名的错误，答案是有的。

所以在传递信息的时候，必须要对信息做一些额外的处理，方便我们来检查信息是否正确，这种检查的信息就叫做校验码，校验码都是冗余信息。

软考中，主要涉及三种校验方式：奇偶校验、CRC循环冗余校验、海明校验。

	校验码	校验码位置	检错	纠错	校验方式
奇偶校验	1	一般拼接在头部，也可以拼接在尾部	可检奇数位错	不可纠错	奇校验：最终的1的个数是奇数个；偶校验：最终1的个数是偶数个
CRC循环冗余校验	拼接在信息位尾部	生成多项式最高次幂决定	可检错	不可纠错	模二除法求余数，拼接作为校验位
海明校验	2r>=m+r+1	插入在信息位中间（2k位置）	可检错	可纠错	分组奇偶校验

校验码-奇偶校验

奇偶校验，可检查1位的错误，不可纠错，并且只能检查奇数位的错误，一般称作检查1位的错误，如果偶数位全的都错了，那么是无法检查出来的。

编码规则

奇偶校验码的编码方法是：由若干位有效信息（如一个字节），再加上一个二进制位（校验位）组成校验码。

奇校验：整个校验码（有效信息位和校验位）中“1”的个数为奇数
偶校验：整个校验码（有效信息位和校验位）中“1”的个数为偶数

比如传递性别，定义男女的编码，男0，女1，定义好编码后，这里的0和1可以称为码字
正常传输： 如果传输的是1，但是接收的是0，这种情况是发现不了错误的，因此需要增加冗余信息帮助我们做校验

经过奇偶校验校验码编码后，后面追加1的个数是奇数还是偶数的校验码，
发送的信息：男00，女11，这种信息传递的时候，我们认为出现错误概率较大的是1位出现错误，比如接收端是男01，或者女10就表示数据是非法的

如果传递女，发送00，奇偶性是满足的，这样是无法判断出数据是否有问题，所以奇偶校验，可检查1位的错误，不可纠错。

什么是纠错的过程？
在二进制传输的过程中，如果明确告诉你第一个数据位置出错了，知道错误的位置，就可以针对它取反进行修正。通俗来讲，就是能找到错误位置，就是可纠错，找不到错误位置，就是不可纠错。

检验码-循环校验码CRC

循环冗余校验（CRC，Cyclic redundancy check），可检错，对数据位不做要求，但是不可纠错。

CRC的编码方式是：在k位信息码之后拼接r位校验码。应用CRC码的关键是如何从k位信息位简单的得到r位校验位（编码），以及如何从k+r位信息吗判断是否出错。考试要求需要掌握算法。

编码规则

循环冗余校验码编码规律如下：

1. 把待编码的N位有效信息表示为多项式M(X)
2. 把M(X)左移K位，得到M(X)×X^K，这样空出了K位，以便拼装K位余数（即校验位）
3. 选取一个K+1位的传声多项式G(X)，对M(X)×X^K做模2除
4. 把左移K位以后的有效信息与余数R(X)做模2加减，拼接为CRC码，此时的CRC码共有K+N位

把接收到的CRC码用约定的生成多项式G(X)去除（生成多项式可以理解为一种惯例，它是发送方和接收方在通信之前就约定好的，所以它是题目已知的），如果正确，则余数位0；如果某一位出错，则余数不为0。不同的位数出错其余数不同，余数和出错位序号之间有唯一的对应关系。

什么是模2除法

特点：
每一位除的结果不影响其它位（无需进位、借位）

模2除法法则：
用除数对被除数最高几位做模2减，没有借位。
除数右移一位，若余数最高位为1，商为1，并对余数做模2减。若余数最高位为0，商为0，除数继续右移一位。
一直做到余数的位数小于除数时，该余数就是最终余数。
补充： 余数为0，则表示传输无差错，否则说明传输过程出现差错。

如何计算校验码

CRC校验码题目一般都是已知信息位，生成多项式也是已知的，我们一般就是求CRC校验码是多少。

例如： 若信息码字为111000110，生成多项式G(X)=X⁵+X³+x+1，计算出的CRC校验码位（）。

解析：
①根据生成多项式求系数二进制
$$G(X)=X^5+X^3+x+1$$
根据生成多项式来求系数二进制
$$G(X)=X^5+0\times X^4+X^3+0\times X^2+x+1$$
X⁵系数为1，X⁴系数为0，X³系数为1，X²系数为0，X¹系数为1，X⁰系数为1。
因此系数二进制=101011

②根据生成多项式的系数，来找余数的位数，有多少位？系数有N位的话，余数就是N-1位，也可以根据生成多项式的最高次幂来决定。
系数有6位，最高次幂是5，因此余数位数是5位。

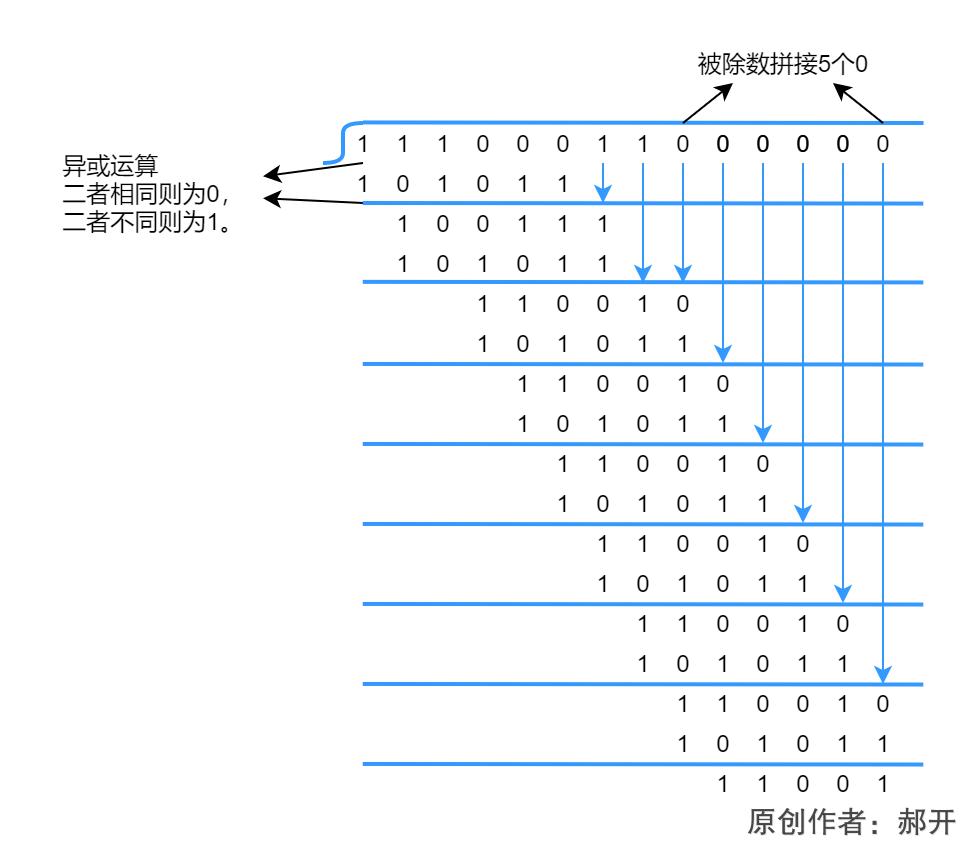
③模2除法，被除数信息位拼接余数位个数的0，也就是②中求得的5个0，因此，被除数=11100011000000，除数是系数二进制=101011，结果是11001。

校验码-海明校验

海明校验是利用交叉校验的方式，形成多组不同的奇偶校验，这种校验如果多组交叉出现问题，可以找到出错的位置。所以海明校验既可检错，也可纠错。它的校验信息是插入在信息位当中2^k的位置，比如2⁰，2¹，2²等等，它的校验方式是多组分组的奇偶校验方式。

海明校验在架构考试中出现的并不多，主要是前两种，掌握怎么计算校验位的位数即可。它的校验位数会根据信息的数据量来决定。
m表示已知的信息位的位数，
$$2^r\ge m+r+1$$

比如，已知需要传递10位信息位数据，需要多少位海明校验码？
假设是3
$$2^3\ge 10+3+1，8\ge 14$$
由此可知，3不满足，需要为4才可以
$$2^4\ge 10+4+1，16\ge 15$$