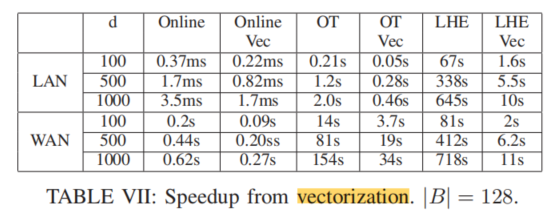
1255. 得分最高的单词集合

题目描述

你将会得到一份单词表 words，一个字母表 letters （可能会有重复字母），以及每个字母对应的得分情况表 score。

请你帮忙计算玩家在单词拼写游戏中所能获得的「最高得分」：能够由 letters 里的字母拼写出的任意属于 words 单词子集中，分数最高的单词集合的得分。

单词拼写游戏的规则概述如下：

玩家需要用字母表 letters 里的字母来拼写单词表 words 中的单词。
可以只使用字母表 letters 中的部分字母，但是每个字母最多被使用一次。
单词表 words 中每个单词只能计分（使用）一次。
根据字母得分情况表score，字母 ‘a’, ‘b’, ‘c’, … , ‘z’ 对应的得分分别为 score[0], score[1], …, score[25]。
本场游戏的「得分」是指：玩家所拼写出的单词集合里包含的所有字母的得分之和。

示例 1

输入：words = [“dog”,“cat”,“dad”,“good”], letters = [“a”,“a”,“c”,“d”,“d”,“d”,“g”,“o”,“o”], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
输出：23
解释：
字母得分为 a=1, c=9, d=5, g=3, o=2
使用给定的字母表 letters，我们可以拼写单词 “dad” (5+1+5)和 “good” (3+2+2+5)，得分为 23 。
而单词 “dad” 和 “dog” 只能得到 21 分。

示例 2

输入：words = [“xxxz”,“ax”,“bx”,“cx”], letters = [“z”,“a”,“b”,“c”,“x”,“x”,“x”], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
输出：27
解释：
字母得分为 a=4, b=4, c=4, x=5, z=10
使用给定的字母表 letters，我们可以组成单词 “ax” (4+5)， “bx” (4+5) 和 “cx” (4+5) ，总得分为 27 。
单词 “xxxz” 的得分仅为 25 。

示例 3

输入：words = [“leetcode”], letters = [“l”,“e”,“t”,“c”,“o”,“d”], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
输出：0
解释：
字母 “e” 在字母表 letters 中只出现了一次，所以无法组成单词表 words 中的单词。

提示

1 <= words.length <= 14
1 <= words[i].length <= 15
1 <= letters.length <= 100
letters[i].length == 1
score.length == 26
0 <= score[i] <= 10
words[i] 和 letters[i] 只包含小写的英文字母。

算法一：二进制枚举

思路

由于题目数据范围不大，因此对于给定的单词表，可以使用 二进制枚举 的方法，枚举出所有的单词组合，然后判断每个单词是否满足题目要求，如果满足则计算其得分，最后取得分数最大的单词组合。
首先使用哈希表记录字母表 letters 中每个字母出现的次数。
接下来，使用二进制枚举的方法，枚举出所有的单词组合，二进制的每一位表示单词表中的每一个单词被选中，如果第 i 位为 1 ，则表示第 i 个单词被选中，否则表示第 i 个单词没有被选中。
然后统计当前单词组合中每个字母出现次数，记录在哈希表中或数组 cur 中，如果 cur 中的每个字母的出现次数都不大于 cnt 中对应字母的出现次数，则说明当前单词组合满足题目要求，我们计算当前单词组合的得分，取得分最大的单词组合。

收获

if(i >> j & 1) ，这个判断条件想了好久，注意是先右移再与，弄反了。其实就是判断当前遍历到的单词 words[j] 需不需要加入组合。比如，组合情况 i=0100，该组合中只需要加入第三个单词，因此当 j=2 时，最低位为 1 ，和 1 相与使得 if 条件成立。

算法情况

时间复杂度：O（2ⁿ * n * M），其中 n 为 words 的数量， M 为 words[i] 的最大长度。
空间复杂度：O（C），其中 C 为 26。

在这里插入图片描述

代码

class Solution {
public:
    int maxScoreWords(vector<string>& words, vector<char>& letters, vector<int>& score) {
        int ans = 0;
        vector<int> cnt(26);
        // 统计字母的个数
        for(auto &ch : letters){
            cnt[ch-'a'] ++;
        }
        int n = words.size();
        for(int i=0; i< 1<<n; ++i){
            // 考虑2^n中所有情况
            vector<int> cur(26);
            for(int j=0; j<n; ++j){
                // j有n个选择（对应n个单词）
                if(i >> j & 1){ 
                    // 确定是否使用该单词，先>>后&
                    for(auto &ch : words[j]){
                        // 如果要使用，统计当前字母个数
                        cur[ch - 'a'] ++;
                    }
                }
            }
            // 用来标记该组合是否满足条件
            bool ok = true;
            int curscore = 0;
            for(int k = 0; k<26; ++k){
                if(cnt[k] < cur[k]){
                    ok = false;
                    break;
                }
                curscore += cur[k] * score[k];  
            }
            if(ok & curscore > ans ){
                // 更新ans
                ans = curscore;
            }
        }
        return ans;
    }
};