1. Motivation

针对机器学习中的出现的数据隐私泄露的风险，提出了线性回归、逻辑回归以及简单神经网络的隐私保护模型。

2. Contributions

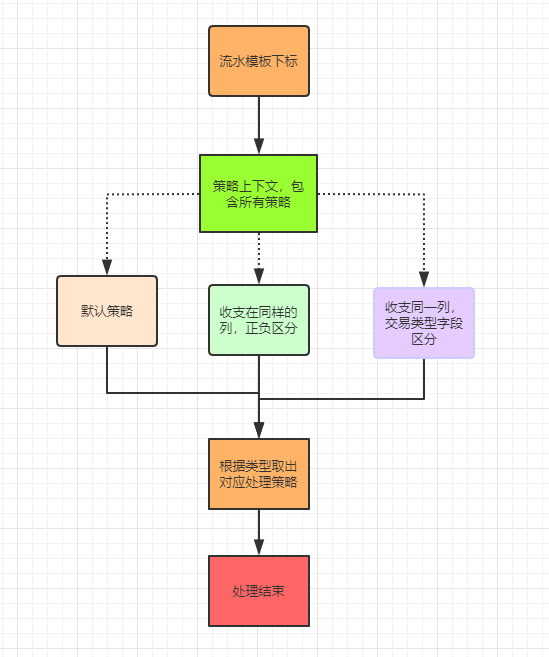
2.1 为线性回归、逻辑回归以及神经网络设计安全计算协议

2.1.1.1 线性回归

线性回归损失函数为：

$\small C(w)=\frac{1}{n}\sum C_i(w)$ , $\small C_i(\mathbf{w})=\frac{1}{2}(\mathbf{x_i}\cdot \mathbf{w}-y_i)^2$

采用SGD算法处理损失函数，权重w的更新公式为：

$\small w_{j}:=w_{j}-\alpha \frac{\partial C_{i}(\mathbf{w})}{\partial w_{j}}$

式子只有加法、乘法运算，秘密分享的形式为：

$\small \langle w_j\rangle:=\left\langle w_{j}\right\rangle-\alpha \operatorname{Mul}^{A}\left(\sum_{k=1}^{d} \operatorname{Mul}^{A}\left(\left\langle x_{i k}\right\rangle,\left\langle w_{k}\right\rangle\right)-\left\langle y_{i}\right\rangle,\left\langle x_{i j}\right\rangle\right)$

写成向量的形式为：

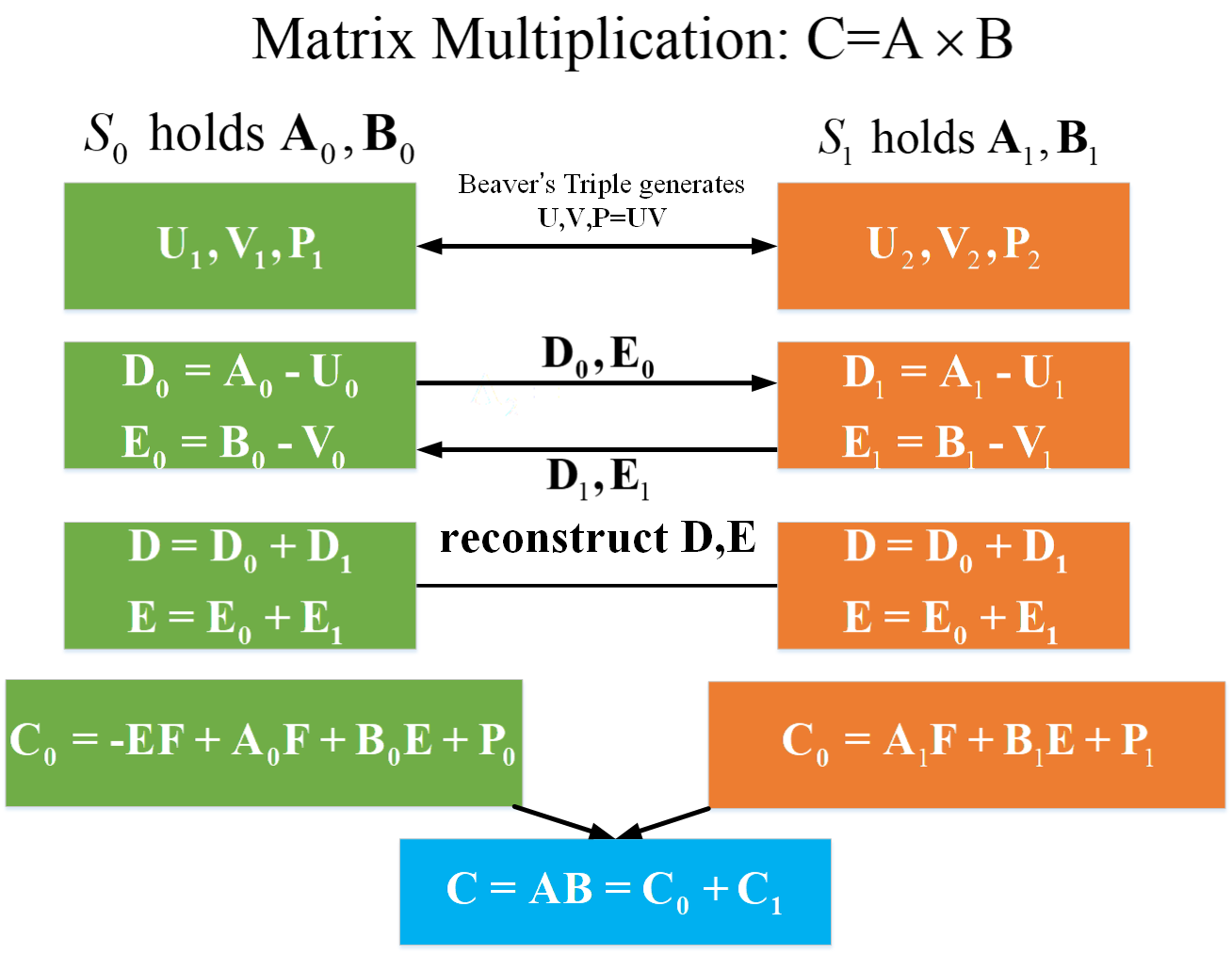
$\small \langle \mathbf{w}\rangle:=\langle \mathbf{w}\rangle-\frac{1}{|B|} \alpha \operatorname{Mul}^{A}\left(\left\langle\mathbf{X}_{B}^{T}\right\rangle, \operatorname{Mul}^{A}\left(\left\langle\mathbf{X}_{B}\right\rangle,\langle\mathbf{w}\rangle\right)-\left\langle\mathbf{Y}_{B}\right\rangle\right)$

根据Beaver's triple 计算矩阵乘法：

这里需要注意的是文章中说明的是两个服务器 $\small S_0,S_1$ ,都以获得数据的一个份额，并不是各方持有一份完整的数据。

可得： $\small \langle\mathbf{C}\rangle_{i}=-i \cdot \mathbf{E} \times \mathbf{F}+\langle\mathbf{A}\rangle_{i} \times \mathbf{F}+\mathbf{E} \times\langle\mathbf{B}\rangle_{i}+\langle\mathbf{Z}\rangle_{i}$ ，之后的乘法运算都依据这个式子。

完整过程如下：

2.2 运算中小数的处理

计算小数乘法，x*y,假设x和y都最多有D为小数。

（1）将x和y进行扩大

$x^{'}=2^{l_D}x$ , $y^{'}=2^{l_D}y$

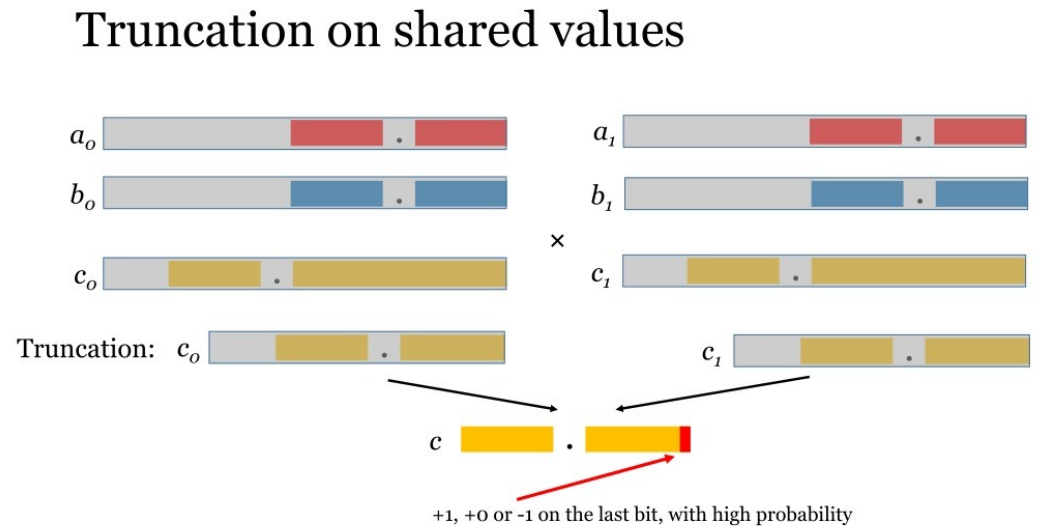
（2）截断小数

扩大后结果为 $z=x^{'}y^{'}$ ,小数位数最多D为，所以将最后D位截取，截断后的结果可写为 $z=z_1\cdot2^{l_D}+z_2$ ，用 $[z]$ 表示截断操作则最的相乘结果为 $z_1$ 。

2.3 优化激活函数

在逻辑回归算法中，有函数 $f()=\frac{1}{1+e^{-x}}$ ,其中在实数域中，该函数包含的除法和求幂运算很难支持2PC和布尔运算，比之前工作用多项式去逼近函数不同的是，作者提出一个Friendly activation function，函数为f(u),f(u)图像如下图所示。

$f(u)=\left\{\begin{array}{ll} 0, & \text { if } u<-\frac{1}{2} \\ u+\frac{1}{2}, & \text { if }-\frac{1}{2} \leq u \leq \frac{1}{2} \\ 1, & \text { if } u>\frac{1}{2} \end{array}\right.\textup{}$

构造的灵感来源于：

（1）函数值应该收敛在0和1之间；（2）RELU函数

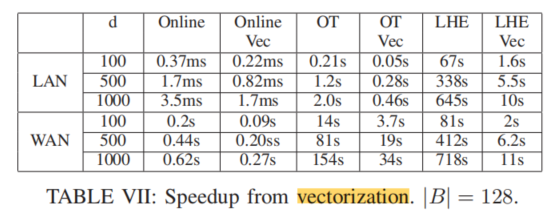
2.4 引入了面向秘密共享的向量化计算

线性回归下模型权重更新公式为 $\small w_{j}:=w_{j}-\alpha \frac{\partial C_{i}(\mathbf{w})}{\partial w_{j}}$ ，仅涉及加法和乘法。秘密分享形式下的加法在本地即可计算，而乘法需要借助Beavers Triple。但是元素级别的运算效率太低，这里优化为矩阵乘法 $C=A\cdot B$ ，由2.1节可知C的Share为： $\small \langle\mathbf{C}\rangle_{i}=-i \cdot \mathbf{E} \times \mathbf{F}+\langle\mathbf{A}\rangle_{i} \times \mathbf{F}+\mathbf{E} \times\langle\mathbf{B}\rangle_{i}+\langle\mathbf{Z}\rangle_{i}$ ，这样可以大大加快计算效率。