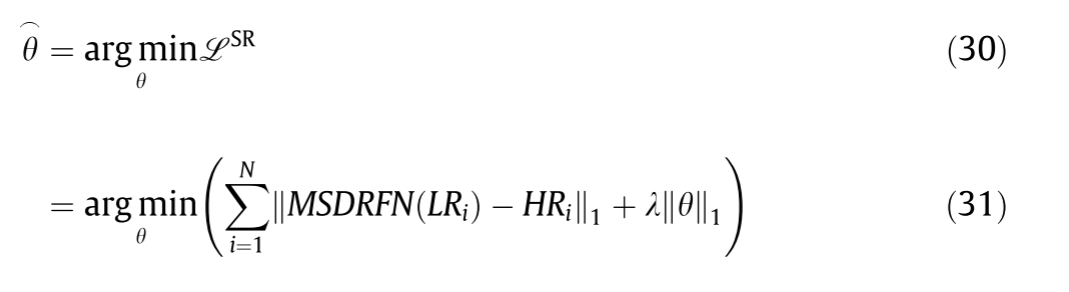😽 PREFACE
🎁欢迎各位→点赞 👍 + 收藏 ⭐ + 评论 📝
📢系列专栏: 算法经典题集
🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用
💪 种一棵树最好是十年前其次是现在
1.递归
1.1 递归实现指数型枚举

下面给出原理分析过程图:
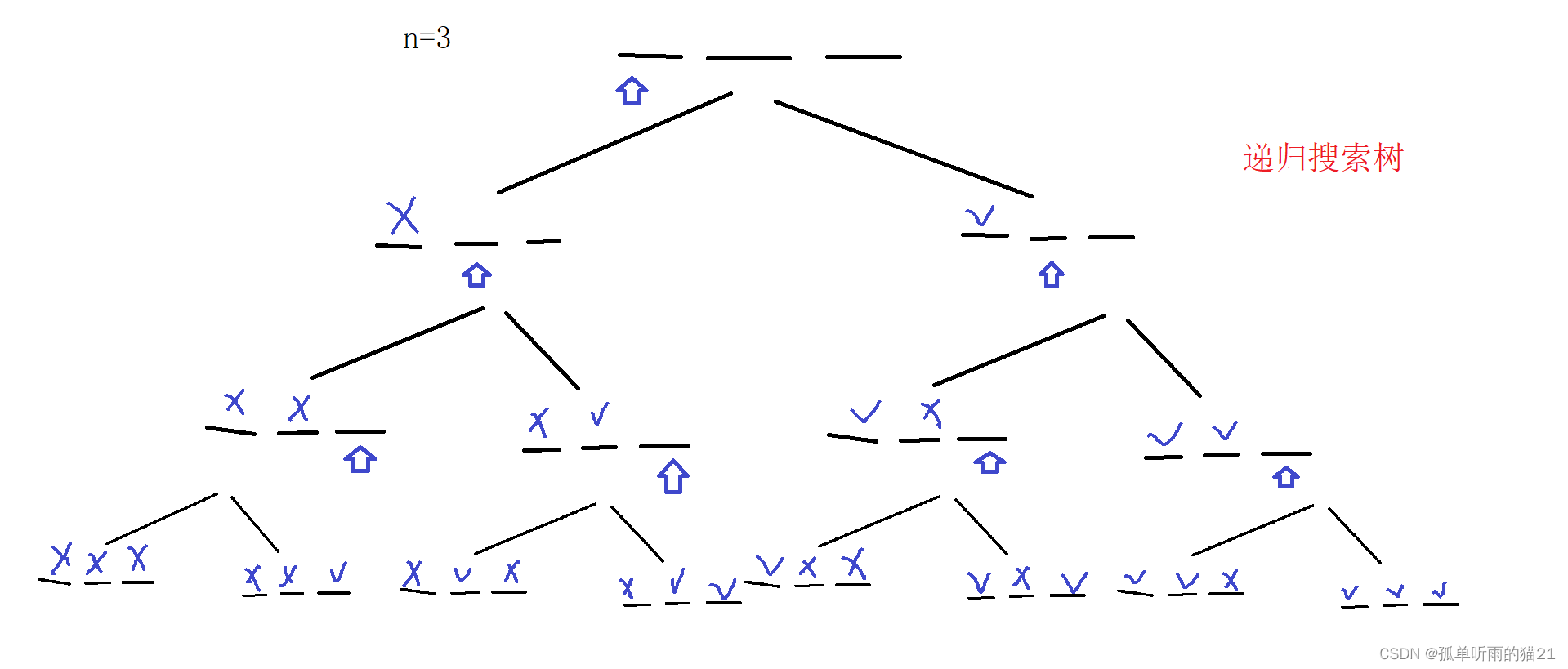
本质就是数学里面的全排列
#include <iostream>
using namespace std;
const int N = 16;
int n;
int st[N];//表示状态:0代表考虑,1代表选择,2代表不选择
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i++)
{
if (st[i] == 1)
{
printf("%d ", i);
}
}
puts("");
return;
}
else
{
st[u] = 1;//选择
dfs(u + 1);
st[u] = 0;//回溯
st[u] = 2;//不选择
dfs(u + 1);
st[u] = 0;//回溯
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}我们也可以优化一下,不用三个状态去表示,采用bool:
#include <iostream>
using namespace std;
const int N = 16;
int n;
bool vis[N];
void dfs(int u)
{
if (u > n)
{
for (int i = 1; i <= n; i++)
{
if (vis[i])
{
printf("%d ", i);
}
}
puts("");
return;
}
else
{
vis[u] = true;
dfs(u + 1);
vis[u] = false;
dfs(u + 1);
}
}
int main()
{
cin >> n;
dfs(1);
return 0;
}其实不然,递归顾名思义,先递下去,还要归回来,
针对这里的代码,可能有些人认为不会执行下面的false:

dfs(u+1)运行之后不是还有个return吗,这时候就会返回上一级函数,执行下面的false子任务

回到递归树上对应的父亲节点,接着遍历父亲的其他儿子。他在这颗子树的遍历中,父亲节点选过的打上标记,子节点才不会选。dfs完相当于把这颗树遍历完了,所以这个树又可以选了。
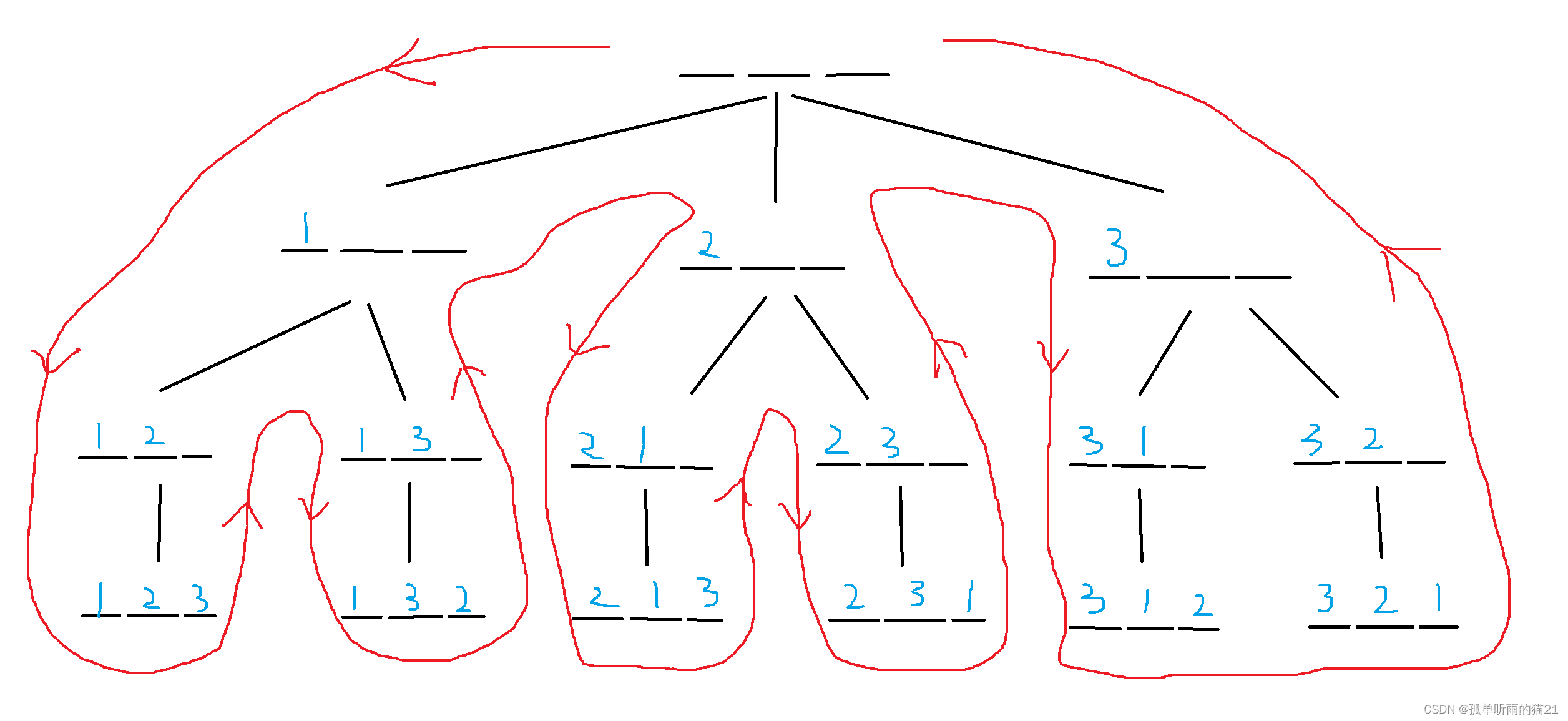
1.2 递归实现排列型枚举

下面给出图解分析过程:
#include <iostream>
using namespace std;
const int N =10;
int path[N];//保存序列
int state[N];//数字是否被使用过
int n;
void dfs(int u)
{
if(u>n)//数字填完了,输出
{
for(int i=1;i<=n;i++)//输出方案
{
cout<<path[i]<<" ";
}
cout<<endl;
return ;
}
else
{
for(int i=1;i<=n;i++)
{
if(!state[i])//如果数字i没有被用过
{
path[u]=i;//放入空位
state[i]=1;//数字被用,修改状态
dfs(u+1);//填下一位
state[i]=0;//回溯,取出i
}
}
}
}
int main()
{
cin>>n;
dfs(1);
return 0;
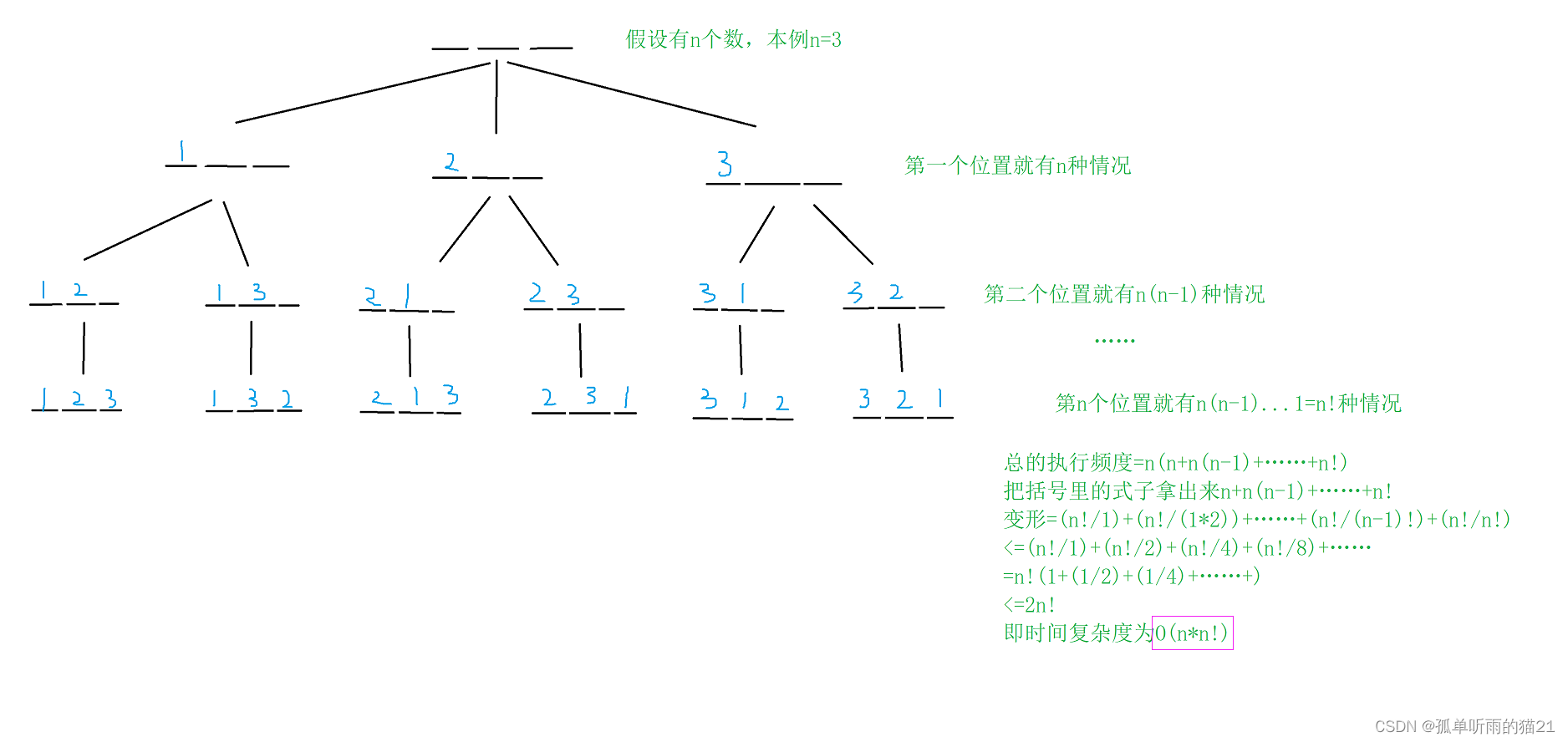
}另外需要注意的是本题的时间复杂度是
下面给出简易的证明:
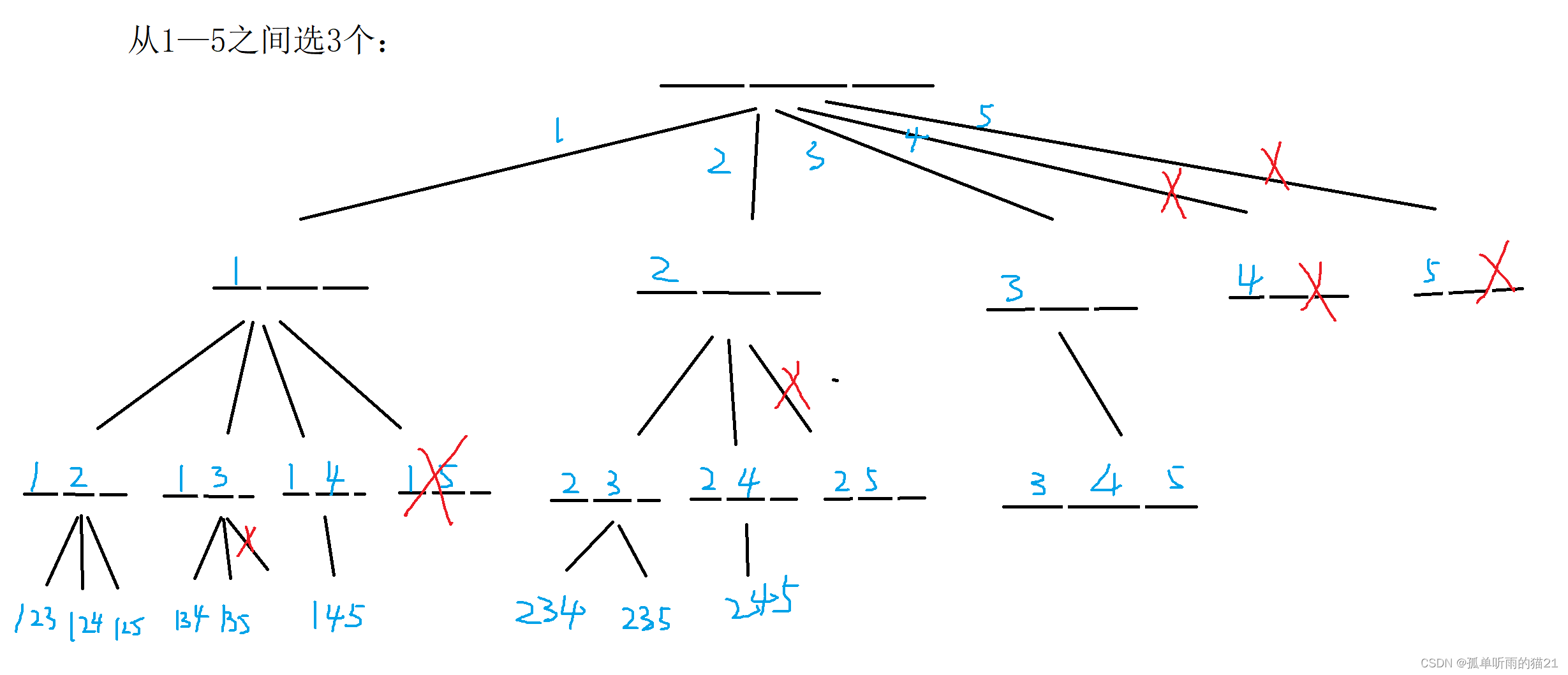
1.3 递归实现组合型枚举

下面给出图解分析过程:
#include <iostream>
using namespace std;
const int N = 30;
int n, m;
int path[N];
void dfs(int u, int s)//u代表当前枚举到哪个位置,s代表当前最小可以从哪个数枚举
{
if (u + n - s < m) return;//剪枝:就算将剩下的数全部选中也凑不齐m个数,所以一定没有答案,所以减掉
if (u == m + 1)
{
for (int i = 1; i <= m; i++) cout << path[i] << " ";
puts("");
return;
}
else
{
for (int i = s; i <= n; i++)
{
path[u] = i;
dfs(u + 1, i + 1);
path[u] = 0;//回溯
}
}
}
int main()
{
cin >> n >> m;
dfs(1, 1);
return 0;
}1.4 带分数

分析过程:

#include <iostream>
using namespace std;
const int N = 10;
int target;//题目条件给的数
int num[N];//用来保存全排列的结果
bool used[N];//生成全排列的过程中标记是否被使用过
int cnt;//计数,最后的输出结果
int calc(int l, int r)//计算num数组中一段的数是多少
{
int res = 0;
for (int i = l; i <= r; i++)
{
res = res * 10 + num[i];//小学数学的加法进位
}
return res;
}
void dfs(int u)//生成全排列
{
if (u == 9)
{
//要把全排列分成三段
for (int i = 0; i < 7; i++)//这里的i是位置,跟else里面的i不同
{
for (int j = i + 1; j < 8; j++)
{
int a = calc(0, i);
int b = calc(i + 1, j);
int c = calc(j + 1, 8);
//这里一定要把除法变成乘法,因为c++里面除法是整除,写成除法的形式容易出错
if (c * target == a * c + b)
{
cnt++;
}
}
}
return;
}
else
{
for (int i = 1; i <= 9; i++)//这里的i是数字
{
if (!used[i])
{
used[i] = true;//只要进if里面来,就是标记使用
num[u] = i;
dfs(u + 1);
used[i] = false;//回溯,还原现场
}
}
}
}
int main()
{
cin >> target;
dfs(0);
cout << cnt << endl;
return 0;
}本题是蓝桥杯某年省赛的原题,下面再给出一个直接调用 next_permutation() 函数的做法,可以代替手写暴搜来枚举全排列,蓝桥杯是可以使用这个函数的
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 10;
int target;
int num[N];
int calc(int l, int r)
{
int res = 0;
for (int i = l; i <= r; i++)
{
res = res * 10 + num[i];
}
return res;
}
int main()
{
cin >> target;
for (int i = 0; i < 9; i++)
{
num[i] = i + 1;
}
int res = 0;
do
{
for (int i = 0; i < 9; i++)
{
for (int j = i + 1; j < 9; j++)
{
int a = calc(0, i);
int b = calc(i + 1, j);
int c = calc(j + 1, 8);
if (a == 0 || b == 0 || c == 0)//特殊情况,需要单独讨论一下
{
continue;
}
if (a * c + b == c * target)
{
++res;
}
}
}
// 调用函数生成全排列
} while (next_permutation(num, num + 9));
cout << res << '\n';
return 0;
}为什么 next_permutation() 函数选用do-while循环结构?
因为你初始化的时候数组是一种情况,直接全排列的话第一种情况直接就少掉了。这也是 next_permutation() 的一个固定方式。
补充: next_permutation() 函数
另外补充一下 next_permutation() 函数的用法:
对于next_permutation函数,其函数原型为:
#include <algorithm>
bool next_permutation(iterator start,iterator end)
如果当前序列不存在下一个排列时,函数返回false,否则返回true
例:将1,2,3,4,5进行全排列
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int num[5] = { 1,2,3,4,5 };
do
{
cout << num[0] << " " << num[1] << " " << num[2] <<" "<<num[3]<<" "<<num[4]<< endl;
} while (next_permutation(num, num + 5));
return 0;
}如果将+5改为+2:
#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
int num[5] = { 1,2,3,4,5 };
do
{
cout << num[0] << " " << num[1] << " " << num[2] <<" "<<num[3]<<" "<<num[4]<< endl;
} while (next_permutation(num, num + 2));
return 0;
}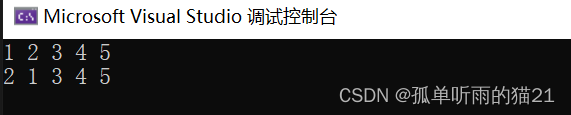
由此可以看出,next_permutation(num,num+n)函数是对数组num中的前n个元素进行全排列,同时并改变num数组的值。
此外,需要强调的是,next_permutation()在使用前需要对欲排列数组按升序排序,否则只能找出该序列之后的全排列数。