大家好,线性回归是确定两种或两种以上变量之间互相依赖的定量关系的一种统计分析方法。根据自变量的个数,可以将线性回归分为一元线性回归和多元线性回归分析。
一元线性回归:就是只包含一个自变量,且该自变量与因变量之间的关系是线性关系。例如通过广告费这一个自变量来预测销量,就属于一元线性回归分析。
多元线性回归:如果回归分析包含两个或以上的自变量,且每个因变量与自变量之间都是线性关系,,则成为多元线性回归分析;例如通过肥料、灌溉等人工成本来预测产量,就属于多元线性回归。
一、线性回归分析的思路
确定因变量与自变量。比如通过人工成本费进行产量预测时,人工成本费是自变量,产量是因变量。
确定线性回归分析的类型。例如在一元线性回归分析中,只需要确定自变量与因变量的相关度为强相关性,即可建立一元线性回归方程,从而确定线性回归分析的类型为一元线性回归。
建立线性回归分析模型。
检验线性回归分析模型的拟合程度。为了判断线性回归分析模型是否可用于实际检测,需要检验线性回归分析模型的拟合程度,也就是对模型进行评估,主要以这三个值作为评估标准:(R-squared统计学中的)、Adj.R-squared(即Adiustd )、P值;其中前两个用来衡量线性拟合的拟合程度,P值用来衡量特征变量的显著性。
利用线性回归分析模型进行预测。如果拟合出来的回归分析模型的拟合度符合要求,就可以使用该模型以及计算出的系数a和b得到回归方程,从而根据已有的自变量数据来预测需要的因变量结果。
二、一元线性回归分析
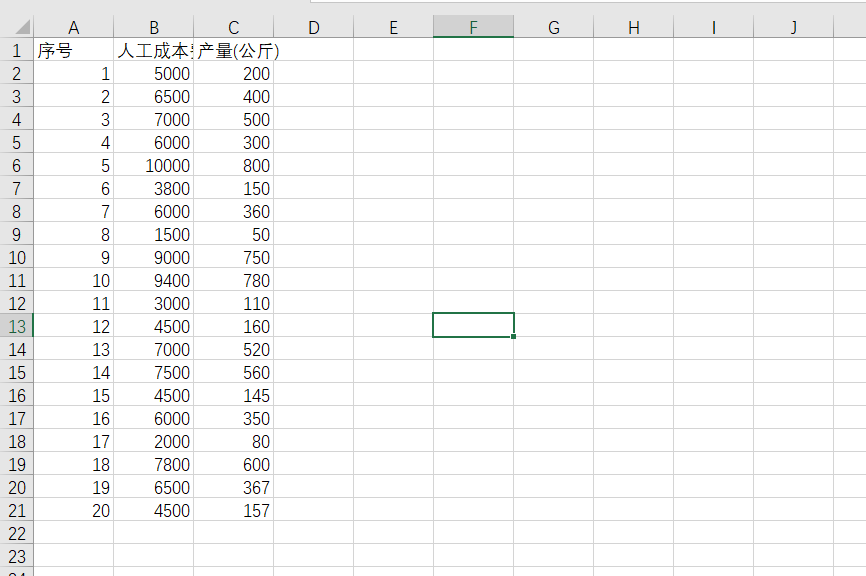
那我们初中学过的一元一次方程y=ax+b来说:就是最简单的一元线性回归,接下来,我们以上图数据为例,假设当人工成本为6600元时,产量为多少?我们下面就这一实际生产问题问题进行一元线性回归分析代码演示。
确定因变量与自变量:
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=0,index_col='序号')
print(data.head())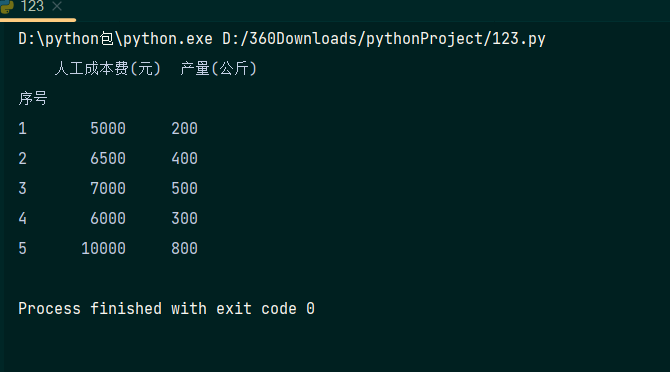
我们要进行的是根据已知的6600人工成本预测产量,由此可知,人工成本费为自变量,产量为因变量。
确定线性回归分析的类型:
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=0,index_col='序号')
print(data.head())
# 选中自变量与因变量的数据,x为自变量,y为因变量
x=data[['人工成本费(元)']]
y=data[['产量(公斤)']]
# 确定线性回归分析的类型
corr=data.corr()
print(corr)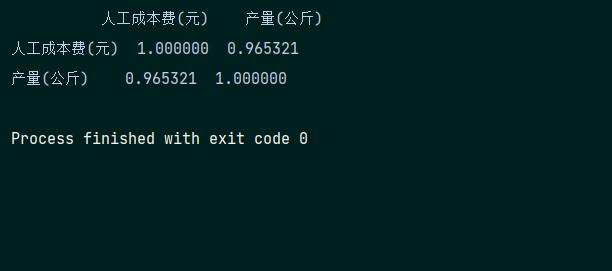
可以看到人工成本与产量之间的相关系数为0.965321,为强相关,随后利用Matplotlib模块进行绘制散点图,代码如下:
# 绘制散点图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.scatter(x,y)
plt.xlabel('人工成本费(元)')
plt.ylabel('产量(公斤)')
plt.show()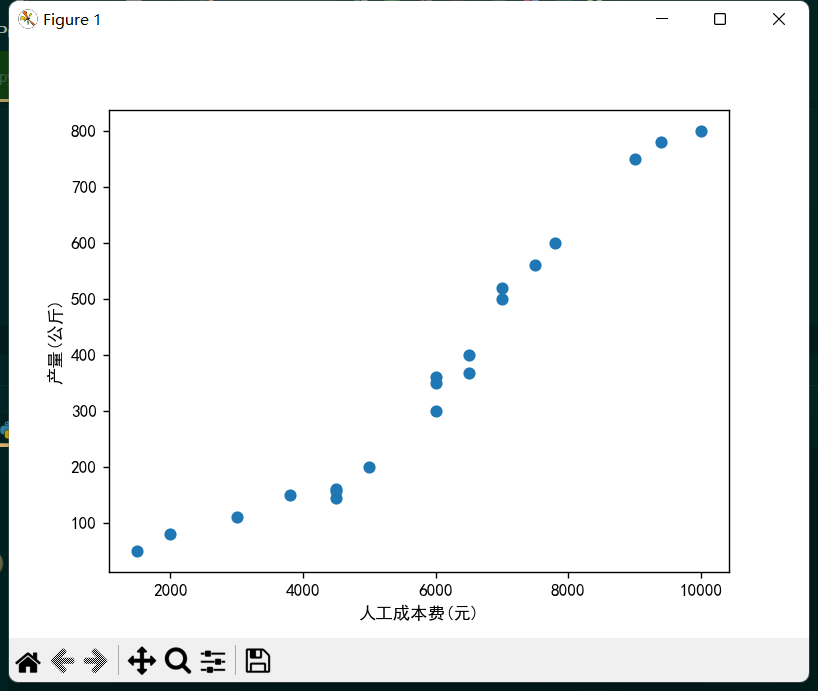
建立回归分析模型以及检验线性回归分析模型的拟合程度:
#建立回归分析模型
from sklearn.linear_model import LinearRegression # 需下载Scikit-Learn模块,使用LinearRegression()函数建立线性回归分析模型
Model=LinearRegression()
Model.fit(x,y)
#检验线性回归分析模型的拟合程度
score=Model.score(x,y)
print(score)
plt.scatter(x,y)
plt.plot(x,Model.predict(x))
plt.xlabel('人工成本费(元)')
plt.ylabel('产量(公斤)')
plt.show()
可以看出模型的评分约为0.93,很接近1,拟合程度还是较高的。
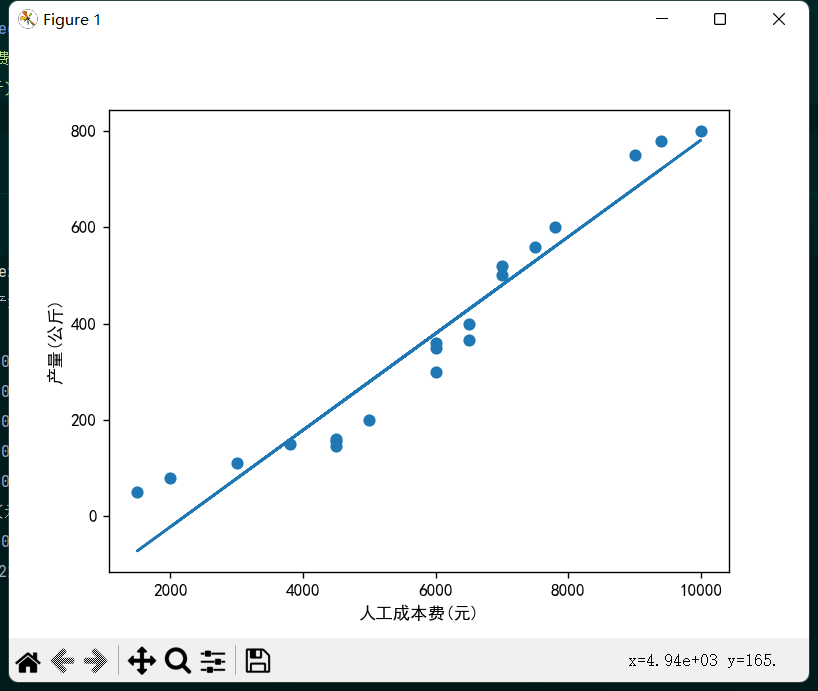
可以看出大多数散点还是比较靠近这条直线的,说明模型很好的捕捉到了数据特征,可以算是恰当拟合。
利用线性回归分析进行预测:
# 预测,也可以进行同时预测多个,如下
y=Model.predict([[6600],[15000],[8888]])
print(y)
三、多元线性回归分析
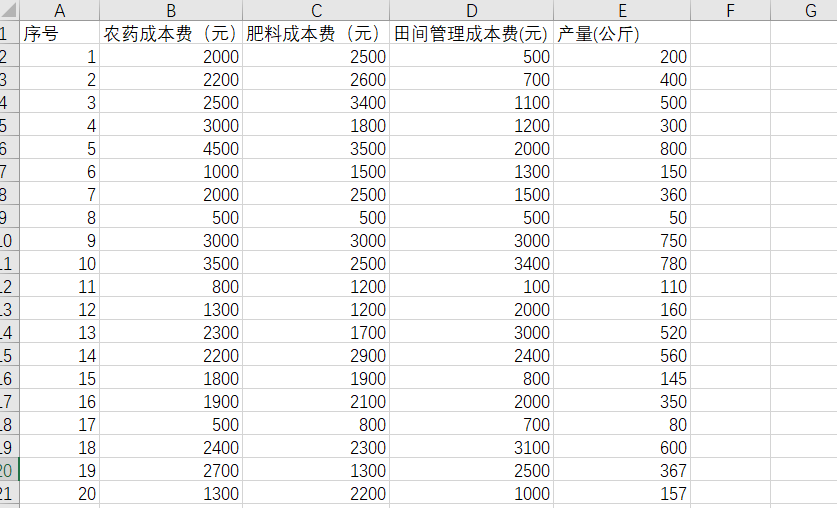
下面我们利用此虚拟数据假设当农药成本费、肥料成本费、田间管理成本费分别为3400、2900、3100时的产量为多少,下面我们将进行完整代码演示:
## 确定自变量与因变量
import pandas as pd
data= pd.read_excel('D:/shujufenxi/作物表型记录本.xlsx',sheet_name=1,index_col='序号')
print(data.head())
# 选中自变量与因变量的数据,x为自变量,y为因变量
x=data[['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)']]
y=data[['产量(公斤)']]
# 确定线性回归分析的类型——图3
corr=data.corr()
print(corr)
# 绘制散点图——图1
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
sns.pairplot(data,x_vars=['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)'],y_vars='产量(公斤)')
plt.show()
#建立回归分析模型
from sklearn.linear_model import LinearRegression # 需下载Scikit-Learn模块,使用LinearRegression()函数建立线性回归分析模型
Model=LinearRegression()
Model.fit(x,y)
#检验线性回归分析模型的拟合程度——图3
score=Model.score(x,y)
print(score)
# 绘制拟合成果图——图2
sns.pairplot(data,x_vars=['农药成本费(元)','肥料成本费(元)','田间管理成本费(元)'],y_vars='产量(公斤)',kind='reg')# kind参数可添加一条最佳拟合直线和95%的置信带,从而更直观的展示模型的拟合程度
plt.show()
# 预测,也可以进行同时预测多个,如下——图3
y=Model.predict([[3400,2900,3100]])
print(y)
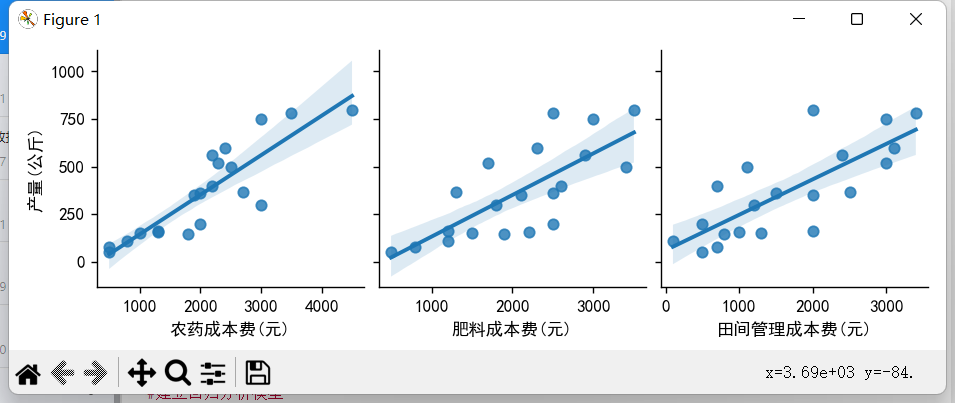
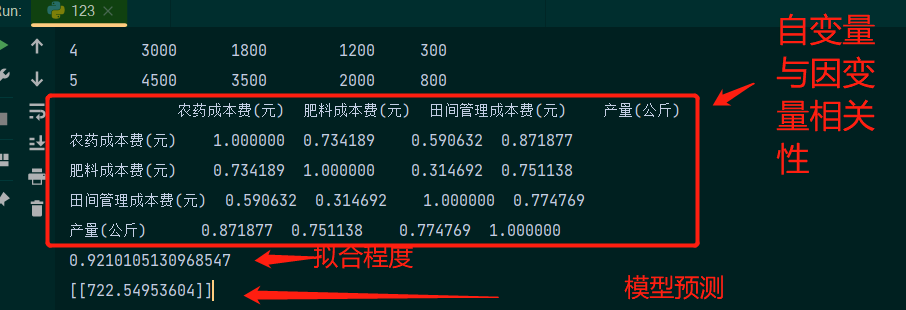
以上就是根据此数据所进行的多元线性回归分析以及模型预测;在上面第二个图中,我们从置信带的宽度来看,农药成本费与产量的线性关系较强,肥料成本费、田间管理成本费两者与产量的线性关系则较弱。
本文所讲对模型进行拟合在实际生产中具有重大意义,不仅可以利用已知变量预测未知变量,还能根据拟合结果判断所得数据是否具有生产意义。