题目描述

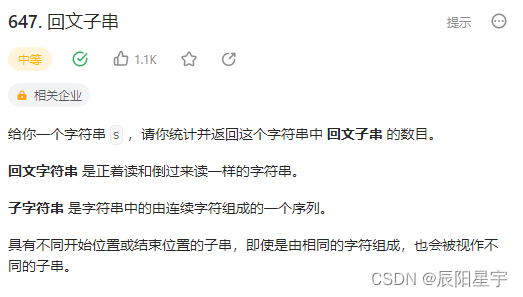
在这里插入图片描述

原题链接：647. 回文子串

解题思路

（1）动态规划

动态规划的思路是每次判定子串两端对称位置是否相等，然后再基于已有的内侧对称情况判定是否为回文串。

动态规划五步曲：

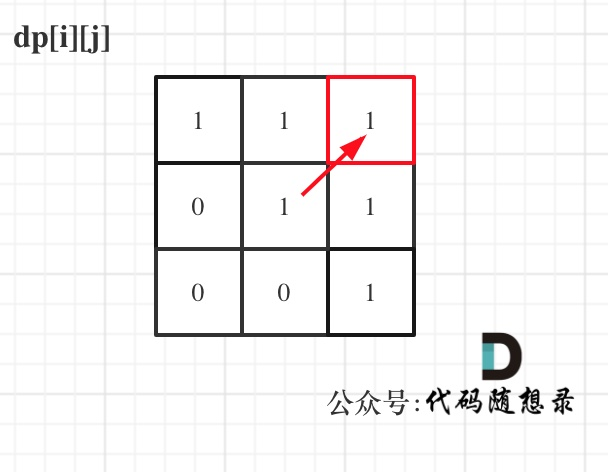
（1）dp[i][j]含义： bool类型变量，s中下标i到下标j之间是否为回文串。

（2）递推公式： 两个状态，三种操作。

1）当遇到s[i]==s[j]时，若此时子串的长度为1或2时（j - i <= 1），此时一定为回文串，执行dp[i][j]=true。如此时子串长度超过2时，则需要根据上一次i与j之间的位置结果进行判定，若dp[i-1][j+1]==true，则再加上当前的情况一定为回文串，执行dp[i][j]=true，否则为false。

2）当遇到s[i]!=s[j]时，执行dp[i][j]=false。

（3）dp数组初始化： dp[i][j] = false，都为进行判定时，为false。

（4）遍历顺序： 因为每次子串为从两边向中间伸缩，因此为从下至上，从左至右。

（5）举例：

class Solution {
public:
    int countSubstrings(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n + 1, vector<bool> (n + 1, false));
        int res = 0;
        for(int i = n - 1; i >= 0; i--) {
            for(int j = i; j < n; j++) {
                if(s[i] == s[j]) {
                    if(j - i <= 1) {
                        dp[i][j] = true;
                        res++;
                    } else if(dp[i + 1][j - 1] == true) {
                        dp[i][j] = true;
                        res++;
                    }
                }
            }
        }

        return res;
    }
};

（2）双指针

双指针的方式是每次从可能会有的回文串中心，然后向两侧进行延伸，判定是否为回文串。当子串为奇数长度时，回文串中心唯一；当子串为偶数长度时，会由两个数作为回文串中心。

class Solution {
public:
    int countSubstrings(string s) {
        int n = s.size(), res = 0;
        for(int i = 0; i < n; i++) {
            // 分别尝试奇数时回文串中心情况和偶数时回文串中心情况
            res += palindromicNums(s, i, i, n);         
            res += palindromicNums(s, i, i + 1, n);
        }

        return res;
    }
    int palindromicNums(const string& s, int i, int j, int n) {
        int res = 0;
        // 从中间向两边伸展探寻
        while(i >= 0 && j < n && s[i] == s[j]) {
            i--;
            j++;
            res++;
        }

        return res;
    }
};