note

求解pagerank：用power iteration（幂迭代）方法求解 $\mathbf{r}=\mathbf{M} \cdot \mathbf{r}$ ( $M$ 是重要度矩阵)
用random uniform teleporation解决dead-ends（自己指向自己）和spider-traps（死胡同节点）问题

文章目录

note
零、内容回顾和本节概况
一、Graph as matrix
二、PageRank
- 2.1 PageRank: The “Flow” Model
- 2.2 PageRank: Matrix Formulation
- 2.3 Connection to Random Walk
- 2.3 Eigenvector Formulation
三、sovle PageRank: Power iteration
- 3.1 power iteration method
- 3.2 解决两大问题：random teleport
四、Random Walk with Restarts & Personalized PageRank
- 4.1 pagerank的变体
- 4.2 小结
五、代码实战：西游记人物重要度
附：时间安排
Reference

零、内容回顾和本节概况

PageRank是1997年谷歌第一代搜索引擎的底层算法。大幅提高了搜索结果的相关率和质量，成为互联网第一个爆款应用，造就了传奇的谷歌公司。
PageRank是搜索引擎、信息检索、图机器学习、知识图谱、线性代数必读经典算法。
PageRank把互联网表示为由网页节点和引用链接构成的有向图，通过链接结构，计算网页节点重要度。来自重要网页节点的引用链接，权重更高。
通过线性方程组、矩阵乘法、特征值和特征向量、随机游走、马尔科夫链，五种角度，理解并求解PageRank值。讲解PageRank的收敛性分析及针对特殊节点的改进方法，最后扩展PageRank在推荐系统中计算节点相似度排序的升级变种。

将图视为邻接着矩阵，从线代角度理解pagerank，和前面task的随机游走和图嵌入学习。
pagerank可用于衡量网络中节点的重要性，即如果一个节点被很多重要节点指向，则说明该节点也是重要节点；通过将图视为邻接矩阵使我们能从三个角度看待pagerank：
- flow model / 线性方程组、
- power iteration（矩阵视角）、
- web surfer随机游走
计算图中节点重要程度：
- PageRank
- Personalized PageRank (PPR)
- Random Walk with Restarts
求解PageRank：power iteration
- 在求解PageRank的过程中会遇到spider traps和dead ends的问题，可以通过random teleport解决。其中M / G 是随机游走的概率转移矩阵。
- Personalized PageRank和Random Walk with Restarts可以衡量node embedding的相似性，区别在于teleport sets。

一、Graph as matrix

我们可以通过上个task3学到的networkx进行pagerank的节点重要程度计算：

import networkx as nx
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
G = nx.star_graph(7)
# nx.draw(G, with_labels = True)
pagerank = nx.pagerank(G, alpha=0.6)
'''
{0: 0.4062486673302485,
 1: 0.08482161895282164,
 2: 0.08482161895282164,
 3: 0.08482161895282164,
 4: 0.08482161895282164,
 5: 0.08482161895282164,
 6: 0.08482161895282164,
 7: 0.08482161895282164}
'''

通过随机游走定义节点重要性、通过matrix factorization获得节点嵌入。

二、PageRank

将网页视为节点，网页之间的超链接视为边；为了简化问题，本task不考虑下面两个问题：
- Dynamic pages created on the fly2
- dark matter：不可达（如有密码等）的database generated pages
- 当今很多超链接是用于执行发布、评论、购买等行为驱动的，作为下个节点的successor；类似的栗子：论文引用，百科词条的相互引用等
节点重要性：in-comng links相比out-going links更不容易造假，视入边越多则节点重要性程度越高；和之前task提及的，是一个递归问题。

2.1 PageRank: The “Flow” Model

为节点j定义指标rank级别： $r_j$ ，其中 $d_i$ 为节点i的出度；因为网页i的重要性是 $r_i$ ，有 $d_i$ 个出边，所以可以定义每个节点（即每个网页）的权重为 $\dfrac{r_i}{d_i}$ 。 $r_j=\sum_{i \rightarrow j} \frac{r_i}{d_i}$
这里节点的权重其实就是对所有加权求和过的入边，累加计算。栗子：1839年的web，其中的 flow等式为 $\begin{aligned} & r_y=r_y / 2+r_a / 2 \\ & r_a=r_y / 2+r_m \\ & r_m=r_a / 2 \end{aligned}$

2.2 PageRank: Matrix Formulation

PageRank的矩阵形式。

随机邻接矩阵stochastic adjacency matrix M：
- $d_i$ ：节点 $i$ 的出度；
- 如果节点 $i$ 指向节点 $j$ 则M矩阵的对应元素值： $M_{j i}=\frac{1}{d_i}$ ；显然M矩阵中每列的元素累加和为1（因为当前列时平均加权元素）。
flow equations： $\boldsymbol{r}=M \cdot \boldsymbol{r}$
上面公式中，等式右边的 $r$ 是rank vector，衡量网页的重要性程度。

在这里插入图片描述

flow等式和矩阵形式：
在这里插入图片描述

2.3 Connection to Random Walk

和随机游走联系。

当从一个web网页节点中进行随机游走， $t$ 时间是在网页 $i$ 上， $t + 1$ 时刻从 $i$ 节点的出边中随机抽取一条边走动；
平稳分布stationary distribution等式： $\cdot p(t)=p(t)$ 其中M是转移概率矩阵，如果达到上面式子这种状态，则 $p (t)$ 是随机游走的平稳分布向量。

2.3 Eigenvector Formulation

特征向量形式。

在之前的task中提到的无向图，直接使用邻接矩阵 $\lambda c=A c$ ，求出该矩阵的特征向量eigenvector，即节点特征，如上个task我们对地铁路线求解每个节点的nx.degree_centrality(G)然后可视化。
PageRank的随机邻接矩阵stochastic adjacency matrix M，flow equation也有类似的特征向量等式（如下），此时的 $r$ 即M的图的平稳分布的一个随机游走： $\cdot r=M \cdot r$

在这里插入图片描述
结论：可通过Power iteration高效求解 $r$ 。

三、sovle PageRank: Power iteration

3.1 power iteration method

方法：power iteration method 幂迭代法求解pagerank

初始赋值： $\boldsymbol{r}^{(0)}=[1 / N, \ldots, 1 / N]^T$
迭代 $\boldsymbol{r}^{(\boldsymbol{t}+\mathbf{1})}=\boldsymbol{M} \cdot \boldsymbol{r}^{(t)}$ ，计算每个节点的pagerank，直到收敛到 $\left(\sum_i\left|r_i^{t+1}-r_i^t\right|<\epsilon\right)$ ，其中 $d_i$ 为节点 $i$ 的出度；迭代式为： $r_j^{(t+1)}=\sum_{i \rightarrow j} \frac{r_i^{(t)}}{d_i}$
迭代停止条件： $\left|\boldsymbol{r}^{(\boldsymbol{t}+1)}-\boldsymbol{r}^{(t)}\right|_1<\varepsilon$ ，这里是范数L1，当然也可以使用其他vector norm方法（如Euclidean等）。
栗子：

在这里插入图片描述

3.2 解决两大问题：random teleport

两大问题：
- spider trap：所有出边都在一个节点组内，会吸收所有重要性，随机游走在圈子中。
- dead end：没有出边，造成重要性泄露
解决方法：random jumps or teleports
- random surfer每一步以概率 $\beta$ 随机选择一条链接（M）, 以概率 $1-\beta$ 随机跳到一个网页上。
  整体公式为: $r_j=\sum_{i \rightarrow j} \beta \frac{r_i}{d_i}+(1-\beta) \frac{1}{N} \quad\left(d_i\right.$ 是节点 $\mathrm{i}$ 的出度)
random jumps or teleports栗子举例：

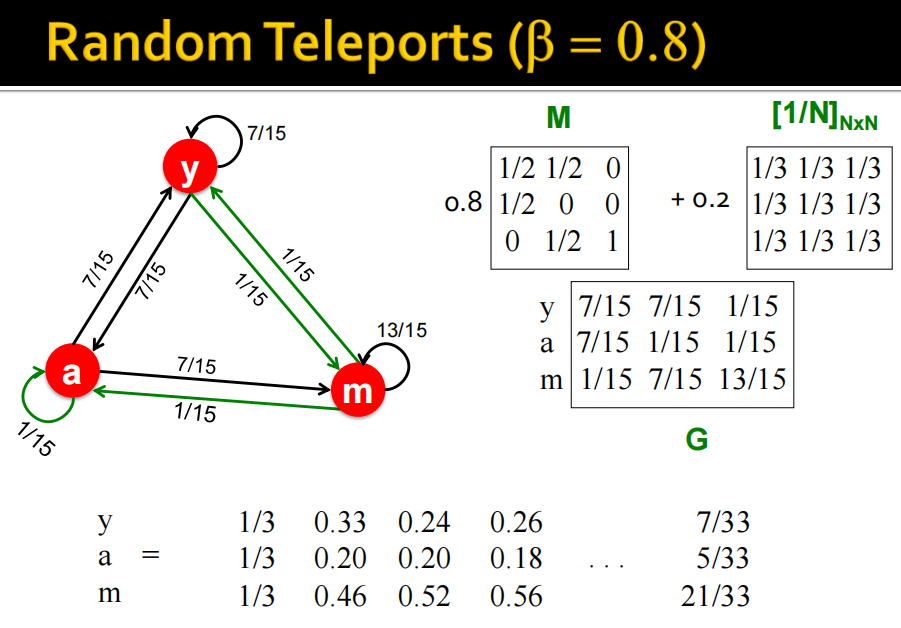
在这里插入图片描述

pagerank结果栗子：
在这里插入图片描述

四、Random Walk with Restarts & Personalized PageRank

4.1 pagerank的变体

在这里插入图片描述

4.2 小结

在这里插入图片描述

五、代码实战：西游记人物重要度

# !/usr/bin/python
# -*- coding: utf-8 -*-
import networkx as nx # 图数据挖掘
import numpy as np # 数据分析
import random # 随机数
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.rcParams['font.sans-serif']=['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
# OpenKG-四大名著人物关系知识图谱和OWL本体：http://www.openkg.cn/dataset/ch4masterpieces

# （一）读取数据和可视化任务关系
# 导入 csv 文件定义的有向图
df = pd.read_csv('data/三国演义/triples.csv')
edges = [edge for edge in zip(df['head'], df['tail'])]
G = nx.DiGraph()
G.add_edges_from(edges)  # 添加有向边

# 可视化
plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, iterations=3, seed=5)
# nx.draw(G, pos, with_labels=True)
nx.draw_networkx(G, pos, with_labels = True)
plt.show()

可以看到人物关系图如下，边是有向边，如head为关羽，tail为刘备是，relation是younger_sworn_brother，label是义弟。
在这里插入图片描述

# （二）计算每个节点的pagerank重要度
pagerank = nx.pagerank(G,                     # NetworkX graph 有向图，如果是无向图则自动转为双向有向图
                       alpha=0.85,            # Damping Factor
                       personalization=None,  # 是否开启Personalized PageRank，随机传送至指定节点集合的概率更高或更低
                       max_iter=100,          # 最大迭代次数
                       tol=1e-06,             # 判定收敛的误差
                       nstart=None,           # 每个节点初始PageRank值
                       dangling=None,         # Dead End死胡同节点
                      )

# 按pagerank重要度进行排序
sorted(pagerank.items(),key=lambda x : x[1], reverse=True)

# （三）设置节点和连接的参数
# 用节点尺寸可视化PageRank值
# 节点尺寸
node_sizes = (np.array(list(pagerank.values())) * 8000).astype(int)
# 节点颜色
M = G.number_of_edges()
edge_colors = range(2, M + 2)
# 绘图
plt.figure(figsize=(15,14))

# 绘制节点
nodes = nx.draw_networkx_nodes(G, pos, node_size=node_sizes, node_color=node_sizes)

# 绘制连接
edges = nx.draw_networkx_edges(
    G,
    pos,
    node_size=node_sizes,   # 节点尺寸
    arrowstyle="->",        # 箭头样式
    arrowsize=20,           # 箭头尺寸
    edge_color=edge_colors, # 连接颜色
    edge_cmap=plt.cm.plasma,# 连接配色方案，可选：plt.cm.Blues
    width=4                 # 连接线宽
)

# 设置每个连接的透明度
edge_alphas = [(5 + i) / (M + 4) for i in range(M)]
for i in range(M):
    edges[i].set_alpha(edge_alphas[i])

# （四）图例
# pc = mpl.collections.PatchCollection(edges, cmap=cmap)
# pc.set_array(edge_colors)
# plt.colorbar(pc)

ax = plt.gca()
ax.set_axis_off()
plt.show()

比如左下角的又大又黄又亮的节点就是诸葛亮，灰常重要。
在这里插入图片描述

附：时间安排

任务	任务内容	截止时间	注意事项
	2月11日开始
task1	图机器学习导论	2月14日周二	完成
task2	图的表示和特征工程	2月15、16日周四	完成
task3	NetworkX工具包实践	2月17、18日周六	完成
task4	图嵌入表示	2月19、20日周一	完成
task5	deepwalk、Node2vec论文精读	2月21、22、23、24日周五	完成
task6	PageRank	2月25、26日周日	完成
task7	标签传播与节点分类	2月27、28日周二
task8	图神经网络基础	3月1、2日周四
task9	图神经网络的表示能力	3月3日周五
task10	图卷积神经网络GCN	3月4日周六
task11	图神经网络GraphSAGE	3月5日周七
task12	图神经网络GAT	3月6日周一

Reference

[1] Pagerank-算法讲解：https://www.bilibili.com/video/BV1uP411K7yN
[2] PageRank代码实战-西游记人物重要度：https://www.bilibili.com/video/BV1Wg411H7Ep
[3] cs224w（图机器学习）2021冬季课程学习笔记4 Link Analysis: PageRank (Graph as Matrix)
[4] CS224W官网：https://web.stanford.edu/class/cs224w/index.html
[5] CS224W-11 成就了谷歌的PageRank
[6] 锋哥笔记-pagerank
[7] 百科-L1范数正则化
[8] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[9] 【经典论文阅读】PageRank原理与实践
[10] Page L, Brin S, Motwani R, et al. The PageRank citation ranking: Bringing order to the web[R]. Stanford InfoLab, 1999.