电子技术——频率补偿

在本节我们介绍修改三极点或多极点放大器的开环增益函数 $A(s)$ 的方法，使得闭环增益在我们希望的值上放大器是稳定的。这个过程称为频率补偿。

理论

最简单的频率补偿方法是引入新的极点，如图下面是一个放大器的伯德图：

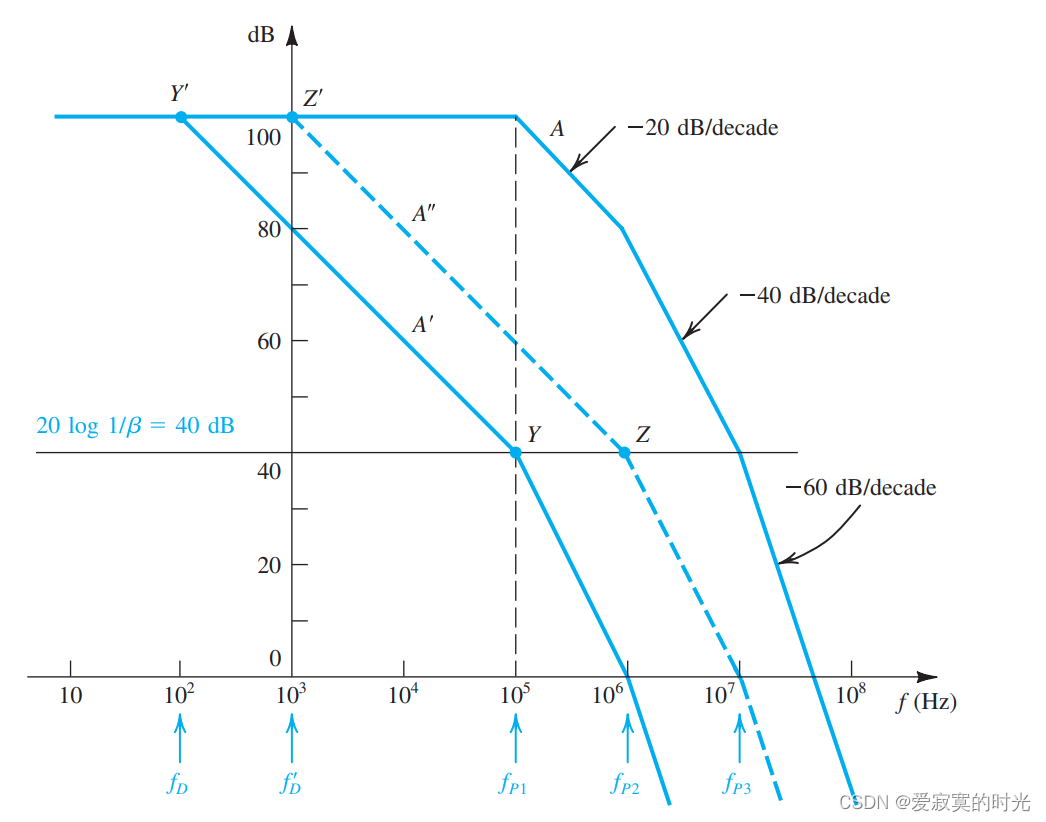
首先我们画出我们期望的 $\beta$ 线，即 $20\log 1/\beta =40dB$ 直线。我们发现该直线并不与 $-20dB/decade$ 区域相交，因此此时的放大器是不稳定的。我们在第一个极点 $f_{P1}$ 与直线的交点 $Y$ 点往上使用 $-20dB/decade$ 线延长至 $A_0$ 的交点 $Y^{\prime }$ 此时的 $Y^{\prime }$ 点就是我们新引入的极点，对应的频率为 $f_D$ ，新的开环增益函数记为 $A^{\prime }(s)$ 。

针对于函数 $A^{\prime }(s)$ 有四个极点 $f_D,f_{P1},f_{P2},f_{P3}$ 。此时 $20\log 1/\beta =40dB$ 直线与 $-20dB/decade$ 区域相交，放大器是稳定的。

这个方法一个严重的缺点是降低了放大器的带宽，这意味着在放大器的高频处其反馈量会急剧下降。因为放大器的品质依赖于反馈量的大小，在高频处反馈质量就会下降。

一种改进的方法是，想办法去掉极点 $f_{P1}$ ，此时极点从 $f_{P2}$ 开始，补偿后对应曲线 $A^{\prime \prime }$ 。我们发现补偿频率点 $f_D$ 前移到 $f_D^{\prime }$ ，带宽得到增加。

尽管没有办法去掉极点 $f_{P1}$ ，但是我们可以让极点 $f_{P1}$ 向左移动到 $f_D^{\prime }$ 处来达到我们的目的。

实现

一般的放大器电路由多阶增益放大器组成，每一阶都会贡献一些极点。通过手动或者计算机分析电路，可以确定极点 $f_{P1}$ 和 $f_{P2}$ 以及其他极点由哪一阶放大器决定。为了方便说明，我们假设第一个极点 $f_{P1}$ 是由于下图中两个差分放大器之间引入的：

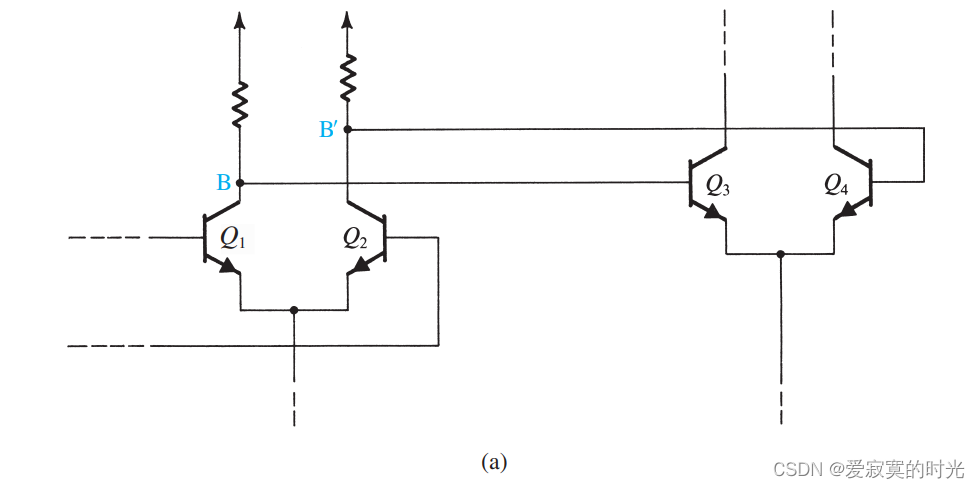
下图展示了等效的传输模型(b)：

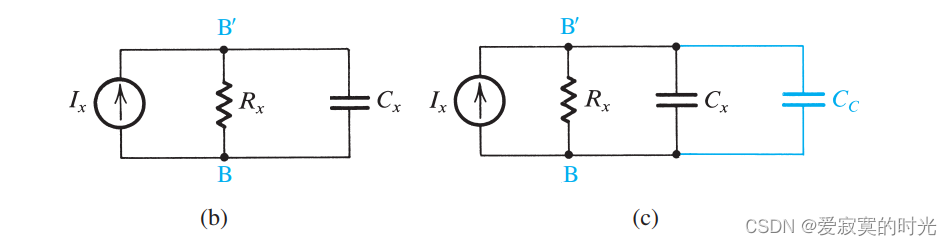
在图中， $I_x$ 是初级差分放大器的输出信号电流， $R_x$ 和 $C_x$ 是从端口 $B{B}^{\prime }$ 看过去的容抗和阻抗，此时极点为：

$$f_{P1}=\frac{1}{2\pi C_x{R}_x}$$

现在让我们在 $B{B}^{\prime }$ 之间引入电容 $C_c$ ，如图©此时的极点变成为：

$$f_{P1}=\frac{1}{2\pi (C_x+C_c)R_x}$$

我们可以选择合适的 $C_c$ 使得 $f_{P1}=f_D^{\prime }$ 。

需要注意的是增加电阻 $C_c$ 可能会影响其他极点的位置，有可能需要计算新的极点位置，继续迭代我们的调整过程，直至达到我们的目的。

这个方法的缺点是 $C_c$ 的值可能很大。因此对于IC类的放大器是不利的，一个更加完美的方法是使用米勒效应进行频率补偿。

米勒补偿和极点分割

下图展示了多阶放大器的其中一阶：

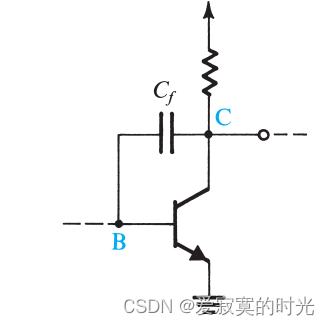
为了方便说明，我们假设此阶放大器为CE放大器，在反馈线路上我们引入 $C_f$ 。下图展示一个等效的电路模型：

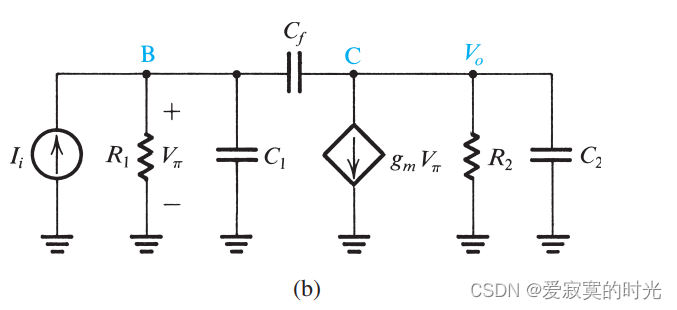
上图中 $I_i$ 是从B点输入的信号电流， $R_1$ 和 $C_1$ 是从B点对地的总阻抗和总容抗，$R_2$ 和 $C_2$ 是从C点对地的总阻抗和总容抗。若没有 $C_f$ 则存在两个输入输出极点：

$$f_{P1}=\frac{1}{2\pi C_1{R}_1}$$

$$f_{P2}=\frac{1}{2\pi C_2{R}_2}$$

考虑当 $C_f$ 存在的时候，我们可以使用米勒等效进行分析，最终我们得到其电路的两个新极点：

$$f_{P1}^{\prime }=\frac{1}{2\pi g_m{C}_f{R}_1{R}_2}$$

$$f_{P2}^{\prime }=\frac{g_m{C}_f}{2\pi C_1{C}_2+C_f(C_1+C_2)}$$

我们发现，随着 $C_f$ 的增加，$f_{P1}^{\prime }$ 将会减小，而 $f_{P2}^{\prime }$ 则会增大，这意味着两个极点会逐渐分开，这个现象称为 极点分割 。注意 $f_{P2}^{\prime }$ 的增大对于我们来说是有益的，因为他拓宽了 $-20dB/decade$ 区域。最终，因为受到米勒效应的影响， $C_f$ 对极点的影响变成了 $g_m{C}_f$ 因此极小的电容就可以实现我们的目标。