论文题目：《CurricularFace: Adaptive Curriculum Learning Loss for Deep Face Recognition》
论文地址：https://arxiv.org/pdf/2004.00288v1.pdf
代码地址：https://github.com/HuangYG123/CurricularFace

建议先了解下这篇文章：MV-softmax

1.背景

       人脸识别中常用损失函数主要包括两类，基于间隔和难样本挖掘，这两种方法损失函数的训练策略都存在缺陷。前一种方法是对所有样本都采用一个固定的间隔值，没有充分利用每个样本自身的难易信息，这可能导致在使用大边际时出现收敛问题；后一种方法则在整个网络训练周期都强调难样本，可能出现网络无法收敛问题。在本论文中，提出了一种新的自适应课程学习损失函数，称为CurricularFace，它能够很好地解决上述两类损失函数存在的问题。
       下图是CurricularFace跟ArcFace和 MV-Arc-Softmax两种方法的对比，可以看到CurricularFace的优势还是很明显的，通过自适应的方式实现，在早期突出易样本的作用（红色虚线），而在晚期突出难样本的作用（红色实线）

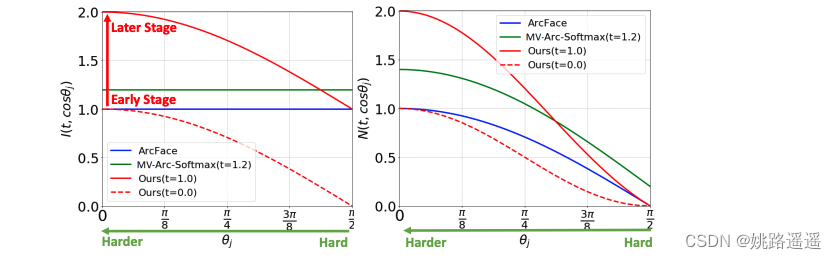
注：Curriculum Learning即课程学习，它是由Montreal大学的Bengio教授团队在2009年的ICML上提出的，其主要思想是模仿人类学习的特点，按照从简单到困难的程度来学习课程，这样容易使模型找到更好的局部最优，同时加快训练速度。

– MV-Sotamax存在的问题：从training起始阶段就开始强调semi-hard/hard-sample，可能会导致模型的收敛问题！

easy sample first, hard sample later!

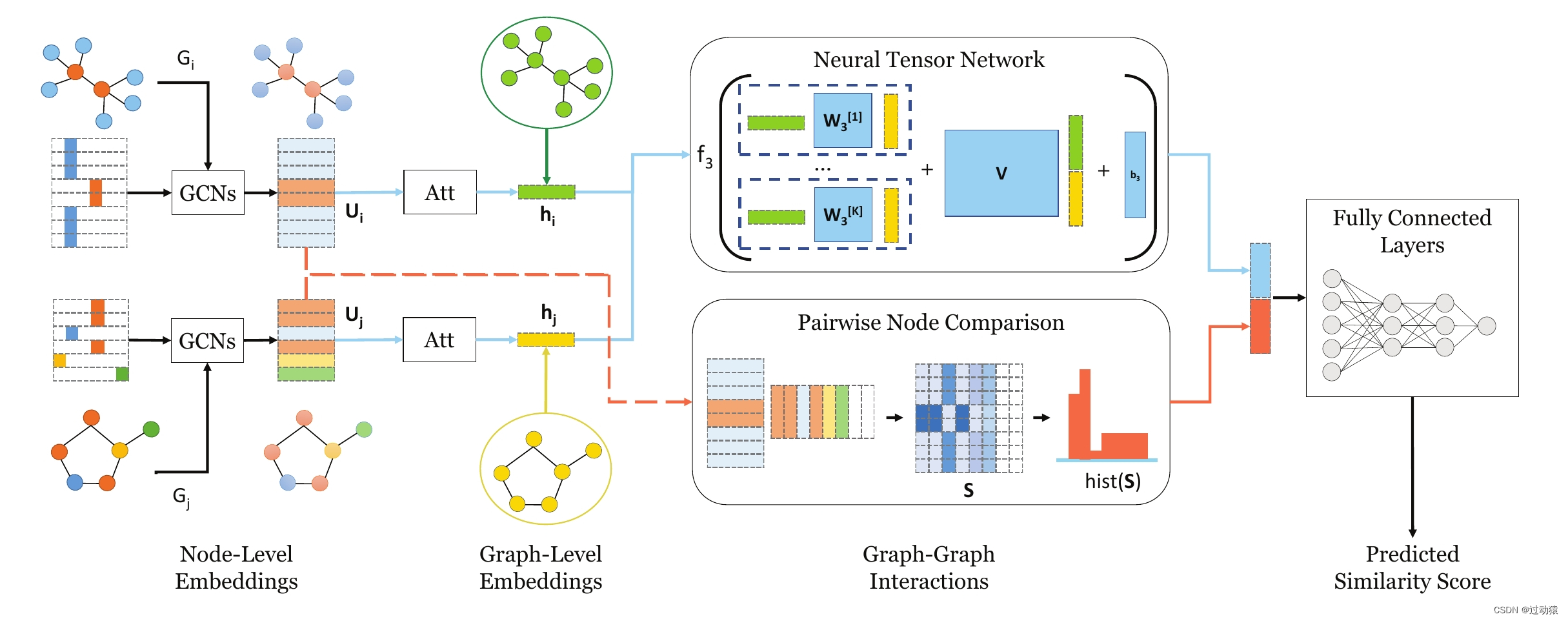
2.方法

       论文中提出的一种新的自适应课程学习损失CurricularFace，是将课程学习的思想嵌入到损失函数中，以实现一种新的深度人脸识别训练策略。该策略主要针对早期训练阶段的易样本和后期训练阶段的难样本，使其在不同的训练阶段，通过一个课程表自适应地调整简单和困难样本的相对重要性。也就是说，在每个阶段，不同的样本根据其相应的困难程度被赋予不同的重要性。
       由于人类学习的本质是先易后难，CurricularFace是以一种适应性的方式将课程学习的理念融入到人脸识别中，这与传统的认知有两处明显不同：
       1）首先，课程设计的自适应性。在传统的课程学习中，样本是按照相应的难易程度排序的，这些难易程度往往是由先验知识定义的，然后固定下来建立课程。而在CurricularFace中，做法是由每个Batch随机抽取样本，通过在线挖掘难样本自适应地建立课程。
       2）其次，难样本的重要性是自适应的。一方面，易样本和难样本的相对重要性是动态的，可以在不同的训练阶段进行调整。另一方面，当前Batch中每一个难样本的重要性取决于其自身的难易程度。
       具体来看，文中选择Batch中的被误分类样本作为难样本，通过调整样本与假类别中心向量之间的余弦相似度的调制系数来加权。为了在整个训练过程中实现自适应课程学习的目标，论文设计了一种新的系数函数，该函数包括以下两个因子：
       1）自适应估计参数t，该参数利用样本和其真类别间的Positive余弦相似度的移动平均值来实现自适应，以消除人工调整的负担。
       2）余弦角度参数,该参数定义难样本实现自适应分配的的难易性。

       上面介绍完了CurricularFace的基本原理，我们来看下其损失函数是如何定义的，如下：

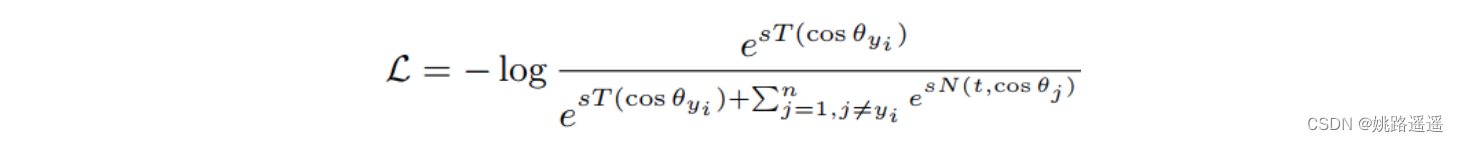
其中，T(cos(θ_y)) = cos(θ_y + m), I (t, cos(θ_j))表示样本的权重函数，N(t, cos(θ_j))定义如下：

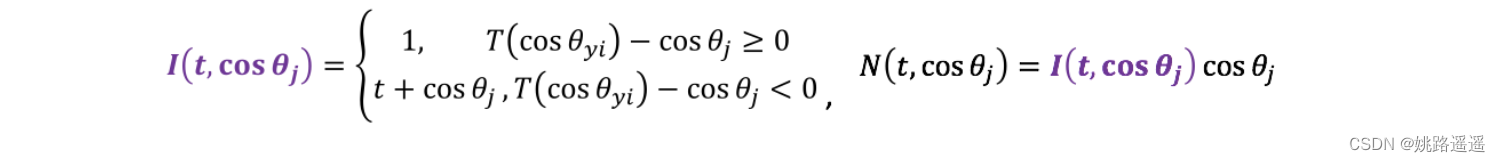
Adaptive Estimation of t.
       在不同的训练阶段决定一个恰当的t的值是十分重要的。理想情况下，t的值能够指示模型的训练阶段。我们通过经验发现正cosine相似度的平均值是一个好的指示器。可是min-batch的基于统计的方法往往面临一个问题：当许多极端数据被采样到一个mini-batch时，统计可能是一个很大的噪声，估计值可能很不稳定。Exponential Moving Average (EMA）方法是一个常用的解决该问题的方法，假设r(k)是第k个batch的正cosine相似度的平均值，r^(0) = 0，即：

则有（t^(k)随着k的增加，会呈现出单调递增的趋势）：



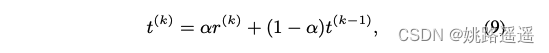
Note : (a, b), a表示在训练过程中[某个时刻] curricular_loss和arcface-loss的比值；b表示max {cos(θ_j), j ≠ yi}

3.训练

3.1.训练步骤

3.2.训练曲线

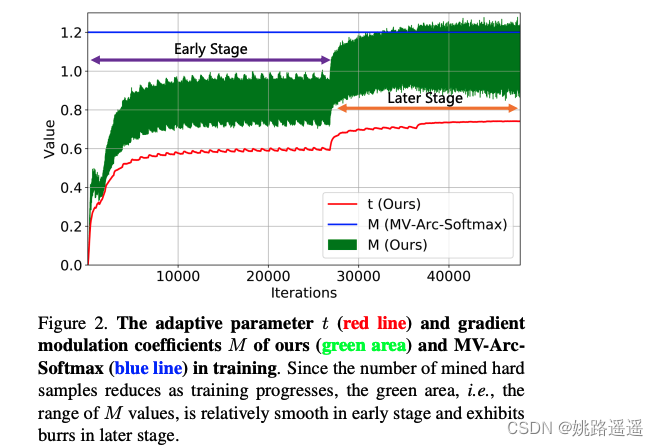
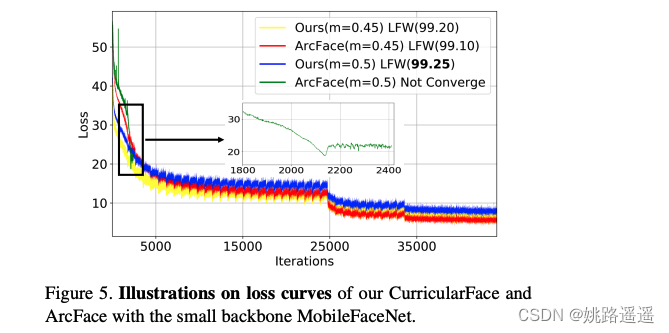
1.x-axis : iterations, y-axis : 难样本的调整系数
2. t：adaptive parameter; M : MV-Arc-Softmax; M(ours) : gradient modulation coefficients
3.在训练早期，t --> 0，模型可以利用easy-sample加速收敛；在训练中后期t不断增大使得I(t, cos(θ_j)) > 1，这样模型可以更多地关注hard-smaples.

4.实验

       从Figure 4中可以看到，在整个训练阶段，CurricularFace对于难样本的决策边界从训练早期到后期自适应性的变化。

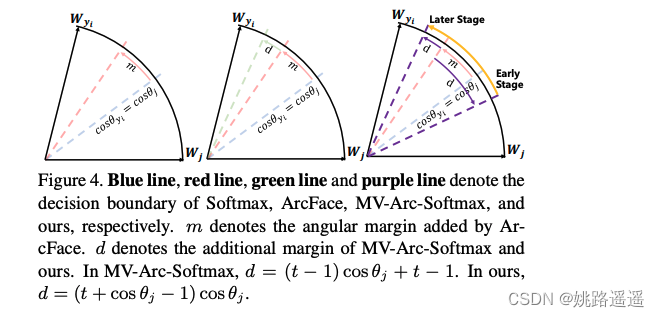
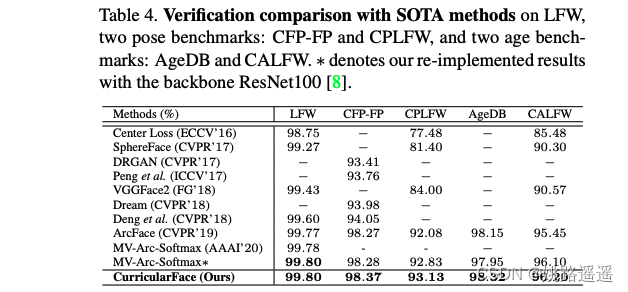
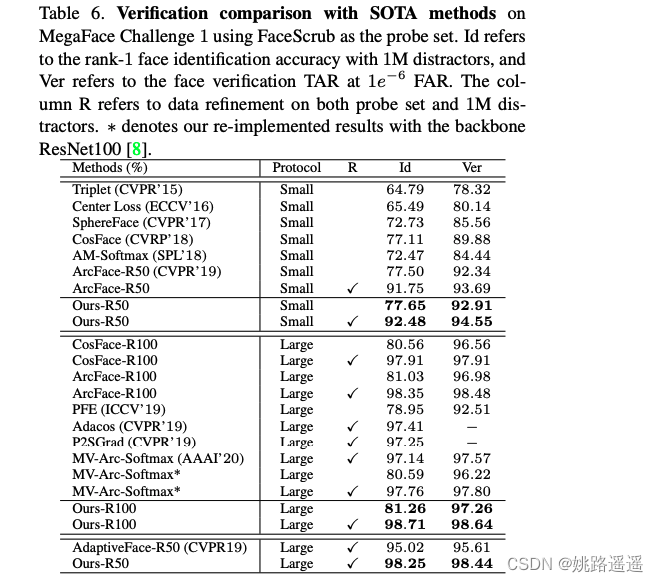
       最终，与其它方法相比，CurricularFace下的人脸识别效果得到明显改善（如Table4与Table6）

5.结论

       论文提出的自适应课程学习损失CurricularFace，将自适应课程学习的思想嵌入到人脸识别中。该方法易于实现，收敛性强，能够明显的提升人脸识别的准确率，而且它解决的是经常在训练过程中出现的问题（如：大边际和难样本），因而具备很高的实用价值。

pytorch代码：

class CurricularFace(nn.Module):
    """Implementation for "CurricularFace: Adaptive Curriculum Learning Loss for Deep Face Recognition".
    """
    def __init__(self, in_features, out_features, device_id=None, m = 0.5, s = 64., fp16 = False):
        super(CurricularFace, self).__init__()
        self.device_id = device_id
        self.fp16 = fp16

        self.m = m
        self.s = s
        self.cos_m = math.cos(m)
        self.sin_m = math.sin(m)
        self.threshold = math.cos(math.pi - m)
        self.mm = math.sin(math.pi - m) * m
     
        self.kernel = Parameter(torch.FloatTensor(out_features, in_features))
        self.register_buffer('t', torch.zeros(1))
        nn.init.xavier_uniform_(self.kernel)     
        #self.kernel = Parameter(torch.Tensor(in_features, out_features))
        #self.register_buffer('t', torch.zeros(1))
        #nn.init.normal_(self.kernel, std=0.01)

    def forward(self, feats, labels):
        #kernel_norm = F.normalize(self.kernel, dim=0)
        #feats = F.normalize(feats)
        #cos_theta = torch.mm(feats, kernel_norm)
        sub_weights = torch.chunk(self.kernel, len(self.device_id), dim=0)
        temp_x = feats.cuda(self.device_id[0])
        weight = sub_weights[0].cuda(self.device_id[0])
        cos_theta = F.linear(F.normalize(temp_x), F.normalize(weight))
        for i in range(1, len(self.device_id)):
            temp_x = x.cuda(self.device_id[i])
            weight = sub_weights[i].cuda(self.device_id[i])
            cos_theta = torch.cat((cos_theta, F.linear(F.normalize(temp_x), F.normalize(weight)).cuda(self.device_id[0])), dim=1)
        cos_theta = cos_theta.clamp(-1.0, 1.0)  # for numerical stability
        with torch.no_grad():
            origin_cos = cos_theta.clone()
        target_logit = cos_theta[torch.arange(0, temp_x.size(0)), labels].view(-1, 1)

        sin_theta = torch.sqrt(1.0 - torch.pow(target_logit, 2))
        cos_theta_m = target_logit * self.cos_m - sin_theta * self.sin_m #cos(target+margin)
        mask = cos_theta > cos_theta_m
        if self.fp16:
            cos_theta_m = cos_theta_m.half()
        final_target_logit = torch.where(target_logit > self.threshold, cos_theta_m, target_logit - self.mm)

        hard_example = cos_theta[mask]
        with torch.no_grad():
            self.t = target_logit.mean() * 0.01 + (1 - 0.01) * self.t
        if self.fp16:
            self.t = self.t.half()
        cos_theta[mask] = hard_example * (self.t + hard_example)
        if self.device_id != None:
            cos_theta = cos_theta.cuda(self.device_id[0])
        cos_theta.scatter_(1, labels.view(-1, 1).long(), final_target_logit)
        output = cos_theta * self.s
        return output