144. 二叉树的前序遍历

难度：$easy$

---

题目描述

给你二叉树的根节点 $root$ ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

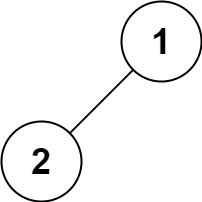
输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

• 树中节点数目在范围 $[0,100]$ 内
• $-100<=Node.val<=100$

进阶： 递归算法很简单，你可以通过迭代算法完成吗？

---

算法1

(递归)

首先我们需要了解什么是二叉树的前序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

定义 preorder(root) 表示当前遍历到 root 节点的答案。按照定义，我们只要首先将 root 节点的值加入答案，然后递归调用 preorder(root->left) 来遍历 root 节点的左子树，最后递归调用 preorder(root->right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

复杂度分析

• 时间复杂度：$O(n)$

• 空间复杂度 : $O(n)$

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    vector<int> res;
    void preorder(TreeNode* root) {
        if (!root) return;

        res.push_back(root->val);
        preorder(root->left);
        preorder(root->right);
    }

    vector<int> preorderTraversal(TreeNode* root) {
        preorder(root);
        return res;
    }
};

---

---

算法2

(迭代)

使用一个栈来进行辅助节点的存储。

复杂度分析

• 时间复杂度：$O(n)$

• 空间复杂度 : $O(n)$

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;

        while (stk.size() || root) {
            while (root) {
                res.push_back(root->val);
                stk.push(root);
                root = root->left;
            }

            root = stk.top()->right;
            stk.pop();
        }

        return res;
    }
};