公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空)，除基层员工外，每个员工都有一个或多个直接下级.

这个公司现在要办party，你可以决定哪些员工来，哪些员工不来，规则：

1.如果某个员工来了，那么这个员工的所有直接下级都不能来

2.派对的整体快乐值是所有到场员工快乐值的累加

3.你的目标是让派对的整体快乐值尽量大

给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

员工信息的定义如下:

class Employee {
    public int happy; // 这名员工可以带来的快乐值
    List<Employee> nexts; // 这名员工有哪些直接下级
}

这道算法题我是花了一整天时间才理清楚的，光靠想象力会把自己给绕晕了。

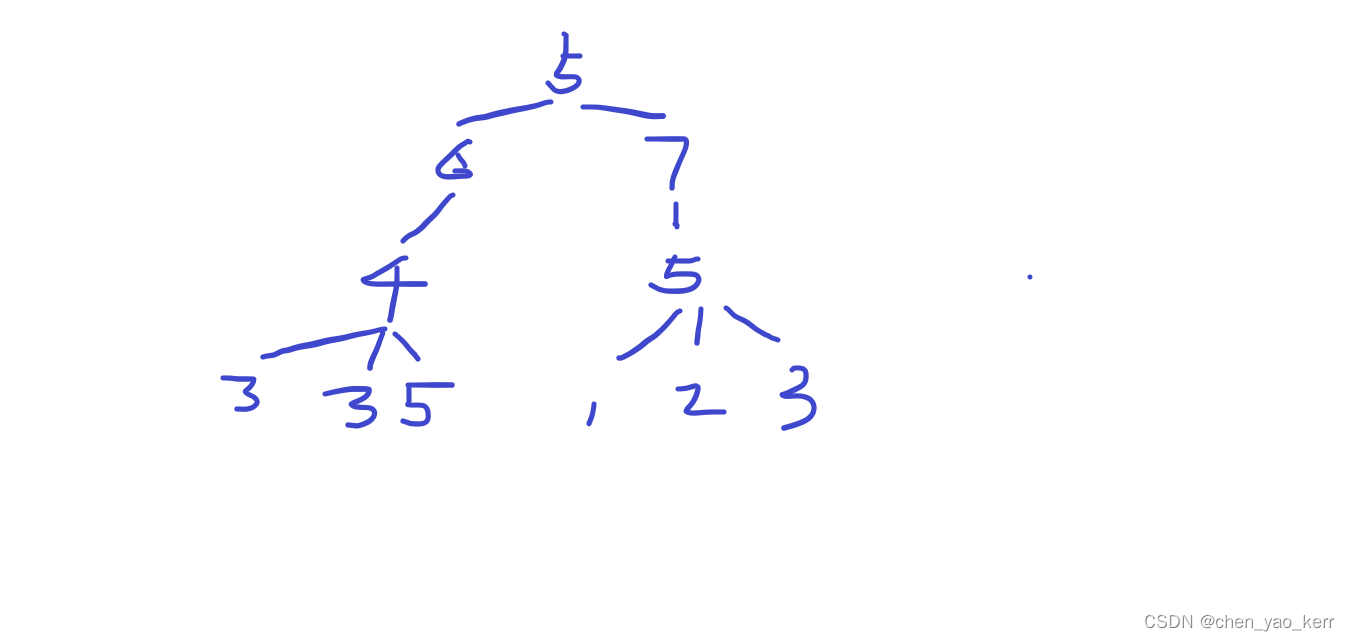
 分析：假设2个变量missMax 和 joinMax分别记录当前节点参加、缺失时有可能获得的最大快乐值

1）叶子节点是没有子节点的，因此我们可知，如果叶子节点不能参加，那么返回的信息就该为0，如果可以参加，那么他们的返回信息就该为当前叶子结点本身的快乐值。

2）左子树4下方有3个节点，分别为3、3、5.

     a) 如果节点4参加，那么子节点就不能参加，因此，当前节点4的最大快乐值为 4，即 joinMax            = 4；missMax =0；

     b) 如果4节点不参加，那么4节点及子节点就有可能获得的最大快乐值为 3+3+5 = 11，即          missMax = 11; 当然，他们的子节点也依旧可能全部不参加，即 joinMax =0;

     c)  总结：如果4节点参加，获得的最宽快乐值为4，即joinMax  = 4， 如果4不参加，获得的最大快乐值为11，即missMax = 11

3）分析6节点

     a) 如果6节点参加，那么4节点就不能参加，那么有可能获得的最大值最大值就为 6 + 11 = 17, 即 joinMax = 17.  这个11是我们第2步b步骤推导出来的

     b) 如果6节点不参加，那么4节点如果参加，因此，最大值就为4，即missMax=4, 由第2步a步骤推导出来。

     c）如果6节点不参加，4节点也不参加，那么4节点的子节点就可以参加了，此时最大快乐值就可得到 3+3+5=11，即missMax = 11

     d)  6不参加，4参加，最大快乐值为4，即missMax=4； 6不参加，4不参加，得到的最大快乐值为11，即missMax = 11。最终，我们可以根据步骤b和c得到6不参加，可以获得的最大快乐值为11，missMax = 11。

     e) 最终6节点，我们可知：6节点参加，最大快乐值可得到17，即 joinMax = 17；6节点不参加，可得到最大快乐值为11，即missMax = 11

下面分析右子树

1. 节点5

      a) 如果5节点参加，最大快乐值为5，即joinMax = 5；

      b) 如果5不参加，那么最大快乐值为 1+2+3 =6； 即 missMax =6；

2. 节点7

   a) 如果节点7参加，那么5就不可以参加，因此最大快乐值为 7+6=13，即joinMax=13，6是由步骤1的b得到

   b)如果7不参加，5也不参加，那么最大快乐值就是6，即missMax=6

   c)如果7不参加，5参加, 那么最大快乐值就是5，即missMax=5 （小于6）

   d) 总结：7参加，可得最大快乐值joinMax=13， 7不参加，可得最大快乐值为missMax=6

 

此时，返回到根节点进行分析，根节点值也为5

a）根节点参加，节点6和7都不能参加。可得到 5 + 11 + 6 = 22

b) 根节点不参加，那么6和7就可以参加了，可得 17 + 13 = 30.

全部理解上面的分析以后，我们再来看看下面的绘图：

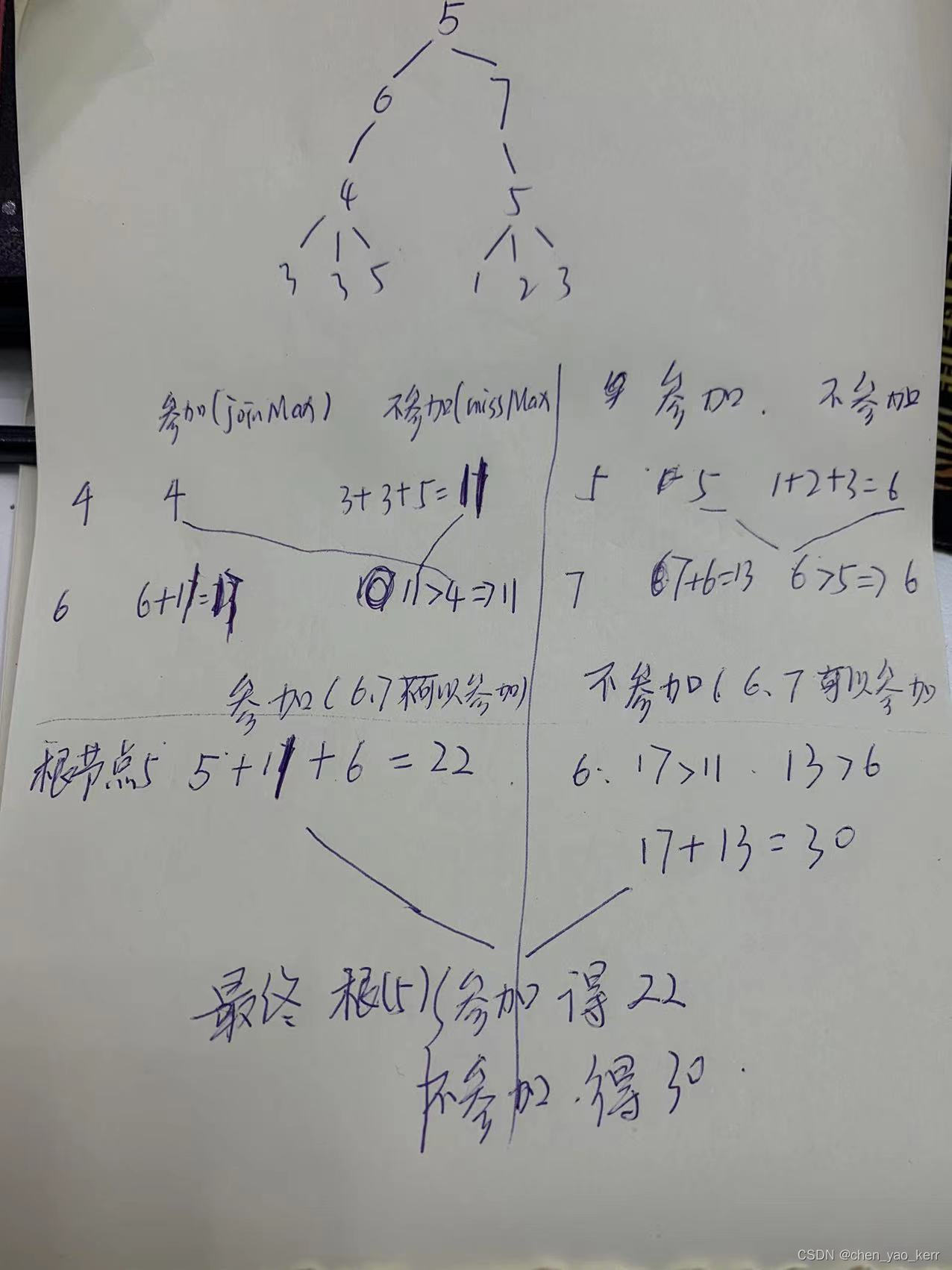
最后，看用套路写代码：

package code03.二叉树_02;

import java.util.ArrayList;
import java.util.List;

/**
 *  公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。
 *  树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。
 *  叶节点是没有任何下属的基层员工(subordinates列表为空)，除基层员工外，每个员工都有一个或多个直接下级。
 *
 *  这个公司现在要办party，你可以决定哪些员工来，哪些员工不来，规则：
 * 1.如果某个员工来了，那么这个员工的所有直接下级都不能来
 * 2.派对的整体快乐值是所有到场员工快乐值的累加
 * 3.你的目标是让派对的整体快乐值尽量大
 * 给定一棵多叉树的头节点boss，请返回派对的最大快乐值。
 */
public class Code12_MaxHappyTree {

    static class Employee {
        int happy;
        List<Employee> nexts;

        Employee (int happy) {
            this.happy = happy;
            nexts = new ArrayList<>();
        }
    }

    public static class Info {
        //当前层参加的值
        public int joinMax;
        //当前层缺失时候的值
        public int missMax;

        public Info(int join, int miss) {
            this.joinMax = join;
            this.missMax = miss;
        }
    }

    public int maxHappy (Employee boss)
    {
        if (boss == null) {
            return 0;
        }

        int join = process(boss).joinMax;
        int miss = process(boss).missMax;

        System.out.println("领导参加， happy值为 ：" + join);
        System.out.println("领导不参加， happy值为 ：" + miss);

        System.out.println("happy的最大值为值为 ：" + Math.max(join, miss));
        return Math.max(join, miss);
    }

    public static Info process(Employee cur) {
        if (cur == null) {
            return new Info(0, 0);
        }

        //记录当前节点参加时的最大快乐值
        int curJoin = cur.happy;
        //记录当前节点不参加时的最大快乐值
        int curMiss = 0;
        for (Employee e : cur.nexts) {
            Info info = process(e);
            //当前层参加，则代表下一层不能参加。因此要获取下一层不能
            //参加情况下的最大快乐值
            curMiss += Math.max(info.missMax, info.joinMax);
            //当前层参加，则获取下一层不参加情况的最大值
            curJoin += info.missMax;
        }

        return new Info(curJoin, curMiss);
    }

    public static void main(String[] args) {

        Employee e31 = new Employee(3);
        Employee e32 = new Employee(3);
        Employee e33 = new Employee(5);
        Employee e3 = new Employee(4);
        e3.nexts.add(e31);
        e3.nexts.add(e32);
        e3.nexts.add(e33);

        Employee e41 = new Employee(1);
        Employee e42 = new Employee(2);
        Employee e43 = new Employee(3);
        Employee e4 = new Employee(5);
        e4.nexts.add(e41);
        e4.nexts.add(e42);
        e4.nexts.add(e43);

        Employee e1 = new Employee(6);
        e1.nexts.add(e3);
        Employee e2 = new Employee(7);
        e2.nexts.add(e4);

        Employee boss = new Employee(5);
        boss.nexts.add(e1);
        boss.nexts.add(e2);

        Code12_MaxHappyTree test = new Code12_MaxHappyTree();
        int a = test.maxHappy(boss);
        System.out.println(a);
    }
}