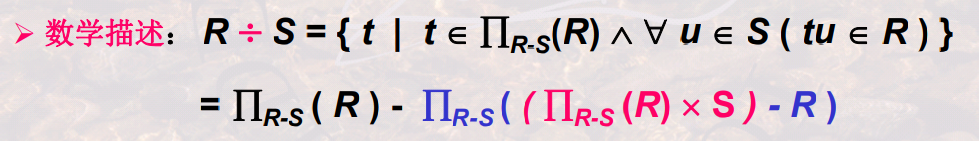第二章 关系数据库
2.1关系数据结构及形式化定义
关系
域(domain) :域是一组具有相同数据类型的值的集合,可以取值的个数叫基数
笛卡尔积 :一个记录叫做一个元组(tuple),元组中每一个属性值,叫一个分量
基数: 域的元素个数
笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尔积,表示为X×Y,所有有序对
假设集合A={a, b},集合B={0, 1, 2},则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。
基数为2 x 3=6

关系: 关系是笛卡尔积的子集,每一行对应一个元组,每一列对应一个域,列名叫做属性(attribute)
R是表的名字,n是属性个数,叫做关系的目或度(degree)
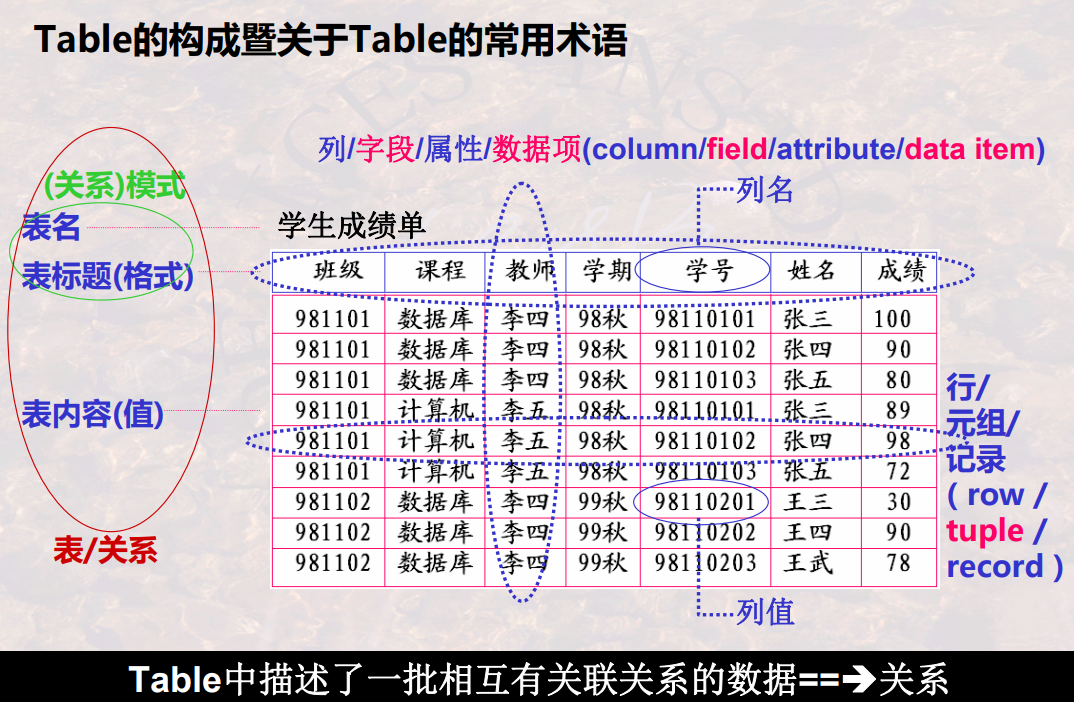
候选码(candidate key): 某一属性组的值能唯一标识一个元组,而他的子集不能,则称该属性组为候选码。
主码(primary key): 若一个关系有多个候选码,则选定其中一个为主码。
主属性: 属于候选码的属性叫主属性。其他属性叫非主属性或非码属性
全码: 若关系模式的所有属性都是这个关系模式的候选码,称为全码。
外码:依赖于另一个关系的主码
关系的三种类型
- 基本关系(基本表/基表):实际存在的表
- 查询表:查询结果对应的表
- 视图表:是由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据
基本关系的6条性质:
- 列是同质的。(同一数据类型)
- 不同的列可以出自同一个域,不同的属性要有不同的属性名
- 列的顺序无所谓。
- 任意两个元组的候选码不能取相同的值。
- 行的顺序无所谓。
- 分量必须取原子值,每一个分量都不可分。
关系模式

或者表示为R(U,D,DOM,F)
R:关系名。
U:组成该关系的属性名的集合。
D: U中的属性所来自的域。
DOM:属性向域的映像集合。
F:属性见数据的依赖关系集合。
关系是关系模式在某一时刻的状态或内容
关系模式是静态的、稳定的,而关系是动态的,随时间不断变化的。
关系数据库
关系数据库的型就是关系数据库模式
关系数据库的值就是关系数据库模式在某一时刻对应的关系的集合
2.2关系操作
特点:集合操作方式,操作对象和结果都是集合
也称为一次一集合的方式,非关系数据库模型的操作方式则成为一次记录的方式
关系数据语言的分类
- 代数方式:关系代数,用关系的运算来表达查询要求
- 逻辑方式:关系演算,用谓词来表达查询要求
- 元组关系演算
- 域关系演算
以上三种方式在表达能力上是等价的,都具有完备的表达能力;它们是抽象的查询语言。与实际的查询语言并不完全一样,但它们能用作评估实际系统中查询语言能力的标准或基础
- 具有关系代数和关系演算双重特点的语言:SQL(Structured Query Language)
SQL是集查询(DQL),数据定义语言(DDL),数据操纵语言(DML)和数据控制语言(DCL)于一体的关系 数据语言
2.3关系的完整性
关系模型中有三类完整性约束:实体完整性,参照完整性和用户定义完整性。
前两个是关系模型必须满足的
实体完整性
若属性A是基本关系R的主属性,那么A不能取空值。
参照完整性
若属性或属性组F是关系R的外码, 它与基本关系S的主码K相对应,则对于R中的每个元组在F上的值必须:
- 或者等于空值(F的每个属性均为空)。
- 或者等于S中某个元组的主码值。
用户定义完整性
用户自定义完整性是针对某一具体关系数据库的约束条件,它反映某一具体应用所涉及的数据必须满足的语义要求。 主要包括非空约束、唯一约束、检查约束、主键约束、外键约束。
2.4 关系代数
关系代数是一种抽象的查询语言,他用对关系的运算来表达查询
三要素: 运算对象(一种关系),运算符,运算结果(一种关系)
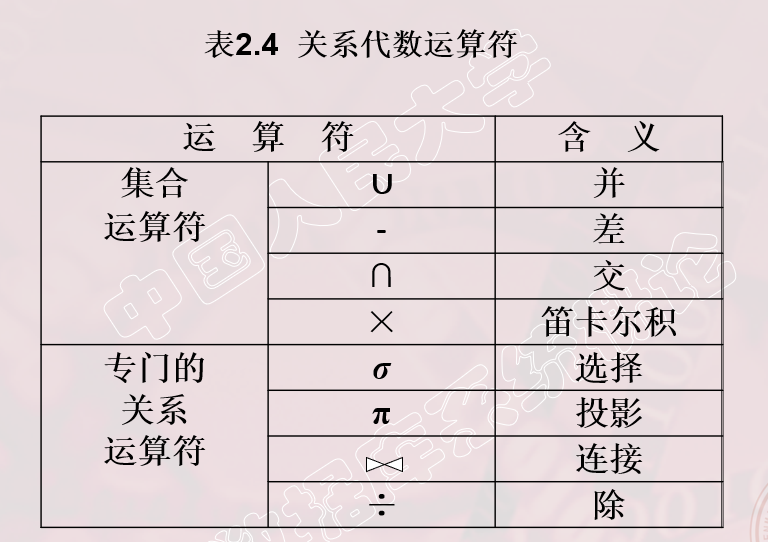
传统的集合运算
并(Union)
R和S
具有相同的目n(即两个关系都有n个属性)
相应的属性取自同一个域
R∪S
仍为n目关系,由属于R或属于S的元组组成
R
∪
S
=
{
t
∣
t
∈
R
∨
t
∈
S
}
R∪S = \{ t|t \in R∨t \in S \}
R∪S={t∣t∈R∨t∈S}
差(difference)
R和S
具有相同的目n
相应的属性取自同一个域
R - S
仍为n目关系,由属于R而不属于S的所有元组组成
R
−
S
=
{
t
∣
t
∈
R
∧
t
∉
S
}
R -S = \{ t|t\in R∧t \notin S \}
R−S={t∣t∈R∧t∈/S}
交(intersection)
R和S
具有相同的目n
相应的属性取自同一个域
R∩S
仍为n目关系,由既属于R又属于S的元组组成
R
∩
S
=
{
t
∣
t
∈
R
∧
t
∈
S
}
R
∩
S
=
R
–
(
R
−
S
)
R∩S = \{ t|t \in R∧t \in S \} \\ R∩S = R –(R-S)
R∩S={t∣t∈R∧t∈S}R∩S=R–(R−S)
笛卡尔积
严格地讲应该是广义的笛卡尔积(Extended Cartesian Product)
R: n目关系,k 1 个元组
S: m目关系,k2 个元组
R×S
列:(n+m)列元组的集合
元组的前n列是关系R的一个元组
后m列是关系S的一个元组
行:k1 × k2 个元组
R
×
S
=
{
t
r
t
s
^
∣
t
r
∈
R
∧
t
s
∈
S
}
R×S = \{\widehat{tr \ ts} |tr \in R ∧ ts \in S \}
R×S={tr ts
∣tr∈R∧ts∈S}
专门的关系符运算
选择(selection)

关系代数中<> 表示不等于
投影(project)

如果有重复的,要去掉
连接(join)
也称为θ-连接

DBMS在进行连接操作的时候,不会先生成笛卡尔积,因此效率更高
对自身的连接,要用到更名

等值连接
当θ为“=” 时,称为等值连接
自然连接
自然连接是一种特殊的等值连接

在自然连接中被舍弃的元组被称为悬浮元组
外连接
如果把悬浮元组保留在结果关系中,而在其他属性上填空值null,那么这种链接就叫做外连接

除(divide)

S 可以有R没有的属性
R ÷ S 和 S 的笛卡尔积 是 R 和S 自然连接 的子集
2.5关系演算
关系元组演算

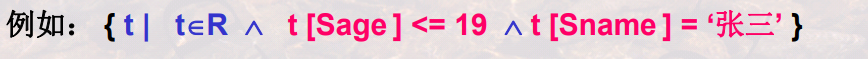
关系域演算