👑作者主页:Java冰激凌
📖专栏链接:数据结构
目录
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先力扣
思路分析
代码
思路拓展
根据一棵树的前序遍历与中序遍历构造二叉树。力扣
思路分析
代码
根据一棵树的中序遍历与后序遍历构造二叉树 力扣
思路分析
代码
二叉树创建字符串力扣
思路分析
代码
思路拓展
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先力扣

思路分析
对于此题 我们的思路是要借助要另一个数据结构 就是我们的栈
首先我们先来分析一波 他可能出现的情况
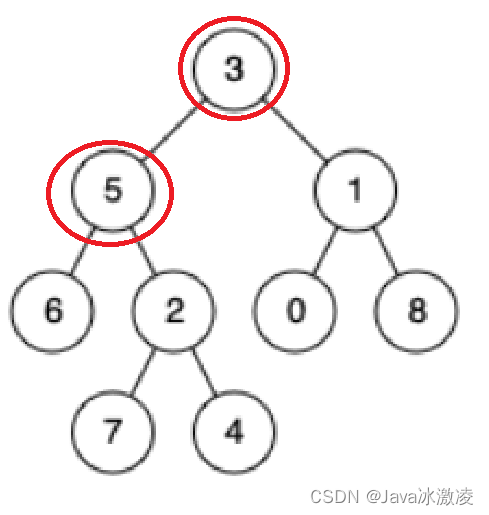
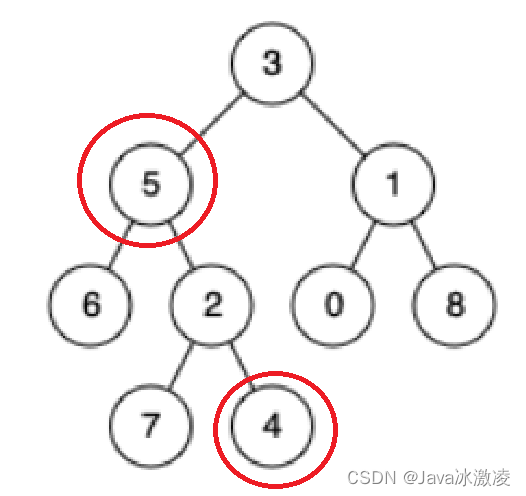
1.其中一个节点是最近的祖先节点 所以说我们的节点3就是我们的最近祖先节点
2.其中一个节点是另一个节点的祖先节点 所以说 我们的5节点是最近的祖先节点
3.最近公共祖先是根节点
我们的思路大概如下:将从根节点到子节点的所有节点都保存到栈中 然后比较两个栈的长度 让栈长度长的先出掉对应个元素 到两个栈节点数量相同时 两个栈同时出节点 当出到了相同节点的时候 这个节点就是我们的最近公共祖先了~
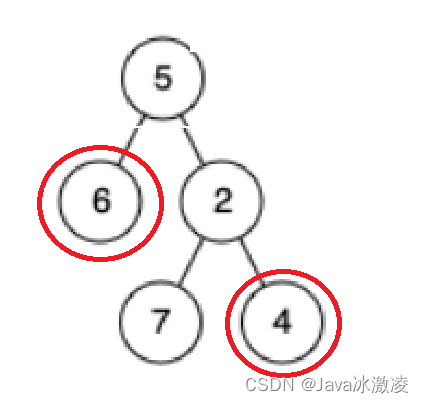
首先我们来将两个节点的路径分别保存到栈中(我们采取先序遍历的思路保存节点)

我们再将两个栈的长度进行对比 长度长的栈先出对应个数的节点 然后我们再同时出节点 直到两个节点相同为止(其中要多考虑的一步是 如果其中一个栈为空 那么代表没有找到对应的节点~ 不过题目中是给出了保证存在的 所以这一步可以不考虑)

代码
public boolean addStack(TreeNode root,Stack<TreeNode> stack, TreeNode node){
if(root == null || node == null){
return false;
}
stack.push(root);
if(root == node){
return true;
}
boolean ret1 = addStack(root.left,stack,node);
if(ret1){
return true;
}
boolean ret2 = addStack(root.right,stack,node);
if(ret2){
return true;
}
stack.pop();
return false;
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Stack<TreeNode> stackp = new Stack<>();
Stack<TreeNode> stackq = new Stack<>();
addStack(root,stackp,p);
addStack(root,stackq,q);
//计算两个栈的长度
int len1 = stackp.size();
int len2 = stackq.size();
if(len1 > len2){
while(len1 - len2 > 0){
len1--;
stackp.pop();
}
}else {
while(len2 - len1 > 0){
len2--;
stackq.pop();
}
}
while(true){
if(stackp.isEmpty()||stackq.isEmpty()){
break;
}
if(stackp.peek() == stackq.peek()){
return stackp.peek();
}
stackp.pop();
stackq.pop();
}
return null;
}算法分析:时间复杂度O(N) 空间复杂度O(N)
思路拓展
提供一个新的思路 我们之前提到过的 树的题一般都是用递归来解的 我们考虑节点是否存在左子树或者右子树 当节点都存在于一颗树的左右子树的时候 那么这个根就是最近公共祖先节点(ps:对于递归的代码 我们要进行划分子问题 学会将一个问题转化为简单问题 并且在思考递归问题的时候
要学会纵向思考 不要将递归展开来想 将递归展开是想不出来的)
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q){
return root;
}
TreeNode left = lowestCommonAncestor(root.left,p,q);
TreeNode right = lowestCommonAncestor(root.right,p,q);
if(left != null && right != null){
return root;
}
if(left == null){
return right;
}
return left;
}算法分析:时间复杂度O(N) 空间复杂度O(N)
根据一棵树的前序遍历与中序遍历构造二叉树。力扣

思路分析
做这道题我们首先需要之前的博客为支撑《数据结构》二叉树(基础题)_Java冰激凌的博客-CSDN博客二叉树基础题https://blog.csdn.net/m0_69996872/article/details/128822826?spm=1001.2014.3001.5501我们先要熟系给定一颗先序遍历树和一颗中序遍历是如何构造一颗二叉树的

我们可知 先序遍历的第一个为根节点 所以我们可以根据这个特性出发 在中序遍历中找到该节点所在位置 找到所在位置后 根据我们之前学到的 在这个节点的左边 都为左子树 右边的都为右子树 所以说 我们可以按照这个思路来分割为递归问题

我们只要按照这个思路依次往下遍历即可~ 是不是恍然大悟!
代码
private int i = 0;
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder == null || inorder == null){
return null;
}
return counst(preorder,inorder,0,inorder.length-1);
}
public TreeNode counst(int[] preorder,int[] inorder,int s1,int s2){
if(s1 > s2){
return null;
}
TreeNode node = new TreeNode(preorder[i]);
int index = findIndex(inorder,s1,s2,preorder[i]);
if(index == -1){
return null;
}
i++;
node.left = counst(preorder,inorder,s1,index-1);
node.right = counst(preorder,inorder,index+1,s2);
return node;
}
public int findIndex(int[] inorder,int s1,int s2,int val){
for(int j = s1; j <= s2;j++){
if(inorder[j] == val){
return j;
}
}
return -1;
}算法分析:时间复杂度O(N) 空间复杂度O(N)
根据一棵树的中序遍历与后序遍历构造二叉树 力扣
思路分析
这个题跟我们刚刚做的一道有异曲同工之妙 我们还是要先有中序遍历和后序遍历绘制二叉树的基础 首先我们知道 后序遍历的最后一个是根节点 所以我们要从最后一个节点出发 所以此处的i就要从最后往前走 其中需要注意到的是 因为后序遍历的是左右根 所以我们在构造的时候 需要先构造右子树再构造左子树
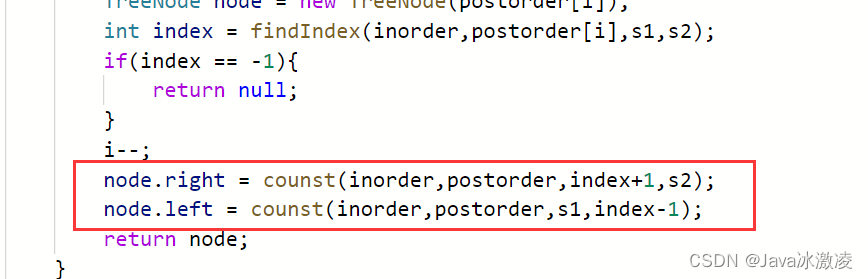
代码
private int i = 0;
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder == null || postorder == null){
return null;
}
i = inorder.length - 1;
return counst(inorder,postorder,0,inorder.length-1);
}
public TreeNode counst(int[] inorder,int[] postorder,int s1,int s2){
if(s1 > s2){
return null;
}
TreeNode node = new TreeNode(postorder[i]);
int index = findIndex(inorder,postorder[i],s1,s2);
if(index == -1){
return null;
}
i--;
node.right = counst(inorder,postorder,index+1,s2);
node.left = counst(inorder,postorder,s1,index-1);
return node;
}
public int findIndex(int[] inorder,int val,int s1,int s2){
for(int j = s1;j <= s2; j++){
if(inorder[j] == val){
return j;
}
}
return -1;
}算法分析:时间复杂度O(N) 空间复杂度O(N)
二叉树创建字符串力扣
思路分析
我们可以先来观察题目
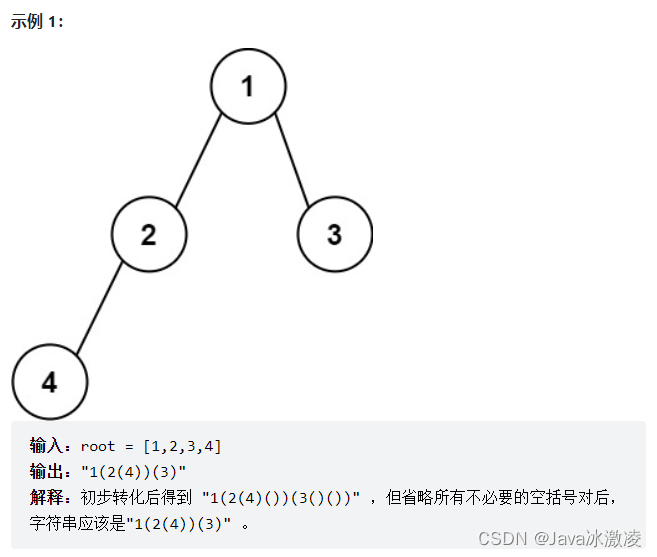
首先我们可以得知~ 当我们左子树或者右子树有节点的时候 我们都需要将值放入括号中
所以我们可以适当的添加判断 当左子树不为空的时候 先添加左括号 当遍历完之后 回到本次递归的时候 继续判断左子树不为空的时候 添加右括号 右子树也是同理
我们来看一下第二个实例
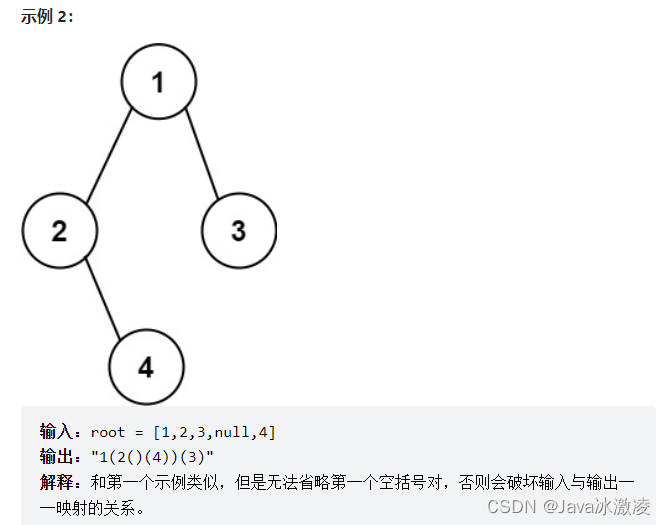
当左子树为空 但右子树不为空的时候 我们是需要适当的添加一对括号的 否则会破坏输入和输出的映射关系
代码
public void _tree2str(TreeNode root,StringBuilder str){
if(root == null){
return ;
}
str.append(root.val);
if(root.left != null){
str.append("(");
}
_tree2str(root.left,str);
if(root.left != null){
str.append(")");
}
if(root.left == null && root.right != null){
str.append("()");
}
if(root.right != null){
str.append("(");
}
_tree2str(root.right,str);
if(root.right != null){
str.append(")");
}
}
public String tree2str(TreeNode root) {
StringBuilder str = new StringBuilder();
_tree2str(root,str);
return str.toString();
}算法分析:时间复杂度O(N) 空间复杂度O(N)
思路拓展
面试官说: 不错 递归遍历写的不错 你能用非递归遍历来做吗?
好的 我们以下的思路首先是最简单的将递归转为非递归的思路 其中我们需要多考虑一个 就是如果使用非递归的话 会存在一个节点被遍历两次 那么这个情况应该如何避免呢 这个时候就需要借助到我们的Set 来做到一个去重 其中一个对于set去重的判断巧用了set.add 返回类型为boolean 如果成功放入返回true 如果失败返回false 还有要注意到的是 我们在头节点的时候 是不需要加左右括号的 所以我们为了方便处理 直接加入判断即可
public String tree2str(TreeNode root) {
StringBuilder str = new StringBuilder();
Stack<TreeNode> stack = new Stack<>();
Set<TreeNode> set = new HashSet<>();
stack.push(root);
while(!stack.isEmpty()){
TreeNode node = stack.peek();
if(!set.add(node)){
if(node != root){
str.append(")");
}
stack.pop();
}else {
if(node != root){
str.append("(");
}
str.append(node.val);
if(node.right != null){
stack.push(node.right);
}
if(node.left != null){
stack.push(node.left);
}else if(node.right != null){
str.append("()");
}
}
}
return str.toString();
}算法分析:时间复杂度O(M+N) 空间复杂度O(N)

![[计算机网络(第八版)]第二章 物理层(章节测试/章节作业)](https://img-blog.csdnimg.cn/0435436cab2240f59dee2cdef567ad8e.png)