文章目录
- 树的度
- 树的性质
- 二叉树的性质
- 二叉树与森林
树的度
树的度指的是树内所有节点的度数的最大值。
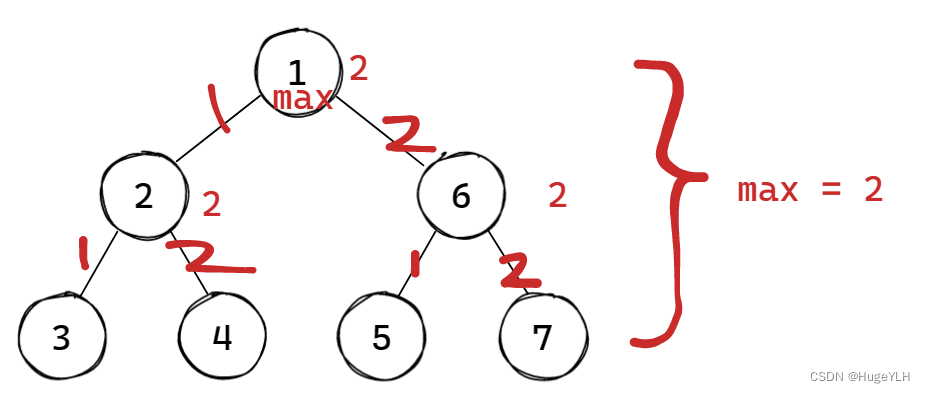
- 节点的度:节点所拥有的子树的数量。简单来说,我们直接数分支即可,例如下图:
在这颗二叉树中,节点2的度为2(他有两个子树),节点6的度为2(他也有两个子树),根节点1的度数也为2(有两个子树),其中叶子节点的度全部为0。
因此度为0的节点一定是叶子节点,度非零,则一定是非叶子节点。
- 树的度:树的度指的是所有的树中的内部节点的度数的最大值。如上图所示,所有节点的度数最大值为2(节点2和节点6和节点1),因此整个树的度为2
树的性质
- 树中所有的节点数等于树的度数+1。如上图所示,所有节点所具有的度数之和为 6,因此节点的总数: n = d+1
- 度为m的树中第 i 层至少有 m^(i-1) 个节点。图中树的度为2,因此m=2。第1层的节点数为1,第2层的节点数为2 ^ 1,第3层的节点数为 2 ^ 2
- 高度为 h 的 m 叉树最多有 (m ^ h - 1)/(m-1)。图中m=2,h=3,因此此树最多有 7 个节点。
- 具有 n 个节点的 m 叉树的最小高度为 logm(n(m-1)+1)。图中 n =7,m=2,因此此树的最小高度为 log2(8) ,因此高度为 3.
二叉树的性质
- 非空二叉树的叶子节点总数等于度为2的节点数+1。 上图中度为2的节点数为3,因此+1得叶子节点的个数为4
- 非空二叉树的第 k 层上最多有 2^k -1 个节点。上图中第 1 层有1个节点,第2层有两个,第3层有四个。
- 高度为 h 的二叉树最多有 2^ h-1 个节点。上图中高度 h =3,因此最多有 7个节点
- 具有n个节点的完全二叉树的高度为 log2(n+1) 或者 [log2(n)]+1。上图中有7个节点,因此高度为 log2(7+1) = 3
二叉树与森林
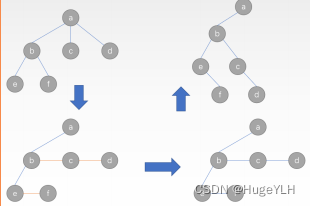
如何将一颗树转换为二叉树?
- 同一节点的各个孩子串联起来。
- 将每个节点的左右分支,从左往右除了第一个以外,全部删除
如何将二叉树转换为树?
- 二叉树从上往下分层,调整成水平方向,左孩子为一层的开始。
- 找到每层的双亲节点,方法为找到与这一层左孩子相连的上一个节点,即是这一层的公共双亲节点。
- 连接双亲节点之后,删除同层的相连关系。
图片演示:
森林的概念:森林是 m 棵 互不相交的树的集合(不一定是二叉树)
如何将森林转换为二叉树?
- 首先将森林中每一棵树转换为二叉树。
- 然后将第二棵树作为第一颗树的右子树,第三棵树作为第二棵树的右子树,以此类推。
如何将二叉树转换为森林?
- 反复断开二叉树的根节点的右孩子子树,直到不存在右孩子指针为止。
森林与二叉树的转换:
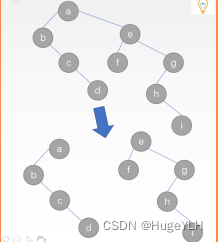
树与森林的遍历:
- 树的先序遍历等于它所对应二叉树的先序遍历
- 树的后序遍历等于它所对应二叉树的中序遍历




![[蓝桥杯 2022 国 B] 卡牌(贪心/二分)](https://img-blog.csdnimg.cn/7c6e3048423c4d58a71683b7a0d2f376.png)



![P1196 [NOI2002] 银河英雄传说 带权并查集](https://img-blog.csdnimg.cn/img_convert/d810383883524a27597d09353c345858.png)