【基础算法】二分例题（我在哪？）

news2024/9/28 10:27:15

🌹作者:云小逸
📝个人主页:云小逸的主页
📝Github:云小逸的Github
🤟motto:要敢于一个人默默的面对自己，强大自己才是核心。不要等到什么都没有了，才下定决心去做。种一颗树，最好的时间是十年前，其次就是现在！学会自己和解，与过去和解，努力爱自己。==希望春天来之前，我们一起面朝大海，春暖花开！==🤟
👏专栏：C++👏 👏专栏：Java语言👏👏专栏：Linux学习👏
👏专栏：C语言初阶👏👏专栏：数据结构👏👏专栏：备战蓝桥杯👏

文章目录

前言
例题：我在哪？
- 题目：
- 输入格式
- 输出格式
- 数据范围
- 输入样例：
- 输出样例：
- 暴力解法（ On4）：
- - 思想：
  - 代码：
- 二分 + STL Set O(n^2^logn)
- - 思想：
  - 代码：
最后

前言

今天这篇文章，我们继续学习二分法，这里讲解有一道有关二分的算法题：我在哪？

——————————————————————————————

首先先写上几句话：献给坚持创作的我和点开这篇文章希望进步的你
1.学不进去的时候就看看这段话：
“你考的不是试，是前途和暮年的欢喜，你桌面上的书本，是将来做选择时的意气和拒绝时的底气。”

2.“要是想哭的话，把能做的事情全部做完之后再尽情地哭。”

3.“我想向自己证明，我从未停止努力，我从未选择放弃，所以我一定能再回顶峰。”

4.“我们每个人都像陨石，即便终将陨落，也请我们尽情燃烧。”

5.“假如你什么都不学习，那就只能生活在现时现世的一个小圈子里，狭窄得很。”

例题：我在哪？

题目：

农夫约翰出门沿着马路散步，但是他现在发现自己可能迷路了！
沿路有一排共 N 个农场。不幸的是农场并没有编号，这使得约翰难以分辨他在这条路上所处的位置。然而，每个农场都沿路设有一个彩色的邮箱，所以约翰希望能够通过查看最近的几个邮箱的颜色来唯一确定他所在的位置。每个邮箱的颜色用 A…Z 之间的一个字母来指定，所以沿着道路的 N
个邮箱的序列可以用一个长为 N 的由字母 A…Z 组成的字符串来表示。某些邮箱可能会有相同的颜色。
约翰想要知道最小的 K 的值，使得他查看任意连续 K 个邮箱序列，他都可以唯一确定这一序列在道路上的位置。
例如，假设沿路的邮箱序列为 ABCDABC 。
约翰不能令 K=3，因为如果他看到了 ABC，则沿路有两个这一连续颜色序列可能所在的位置。

最小可行的 K 的值为 K=4，因为如果他查看任意连续 4 个邮箱，那么可得到的连续颜色序列可以唯一确定他在道路上的位置。

输入格式

输入的第一行包含 N，第二行包含一个由 N 个字符组成的字符串，每个字符均在 A…Z 之内。

输出格式

输出一行，包含一个整数，为可以解决农夫约翰的问题的最小 K 值。

数据范围

1≤N≤100

输入样例：

7
ABCDABC

输出样例：

4

暴力解法（ On4）：

思想：

可以直接进行枚举两个子串并比较，如：
写四个for循环：
第一个：先枚举k
第二个：枚举其中任意一个子串，k值一定，只要枚举起点就可以了
第三个：再枚举第二个子串，
第四个：判断两个子串是否相同：
N最大是100，四次方是1个亿，刚好可以过：而且它是达不到最大一个亿的，有的时候直接break了
在这里插入图片描述

代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int n;
string str;

int main()
{
    cin >> n >> str;

    for (int k = 1; k <= n; k ++ )//先枚举k
    {
        bool flag = false;
        for (int i = 0; i + k - 1 < n; i ++ )//枚举其中任意一个子串，k值一定，只需要枚举起点就可以了
        {
            for (int j = i + 1; j + k - 1 < n; j ++ )//再枚举第二个子串
            {
                bool same = true;
                for (int u = 0; u < k; u ++ )//判断两个子串是否相同
                    if (str[i + u] != str[j + u])
                    {
                        same = false;
                        break;
                    }
                if (same)
                {
                    flag = true;
                    break;
                }
            }
            if (flag) break;
        }

        if (!flag)
        {
            cout << k << endl;
            break;
        }
    }

    return 0;
}

在这里插入图片描述

二分 + STL Set O(n²logn)

思想：

判断是否可以二分，要看它是否有二段性：
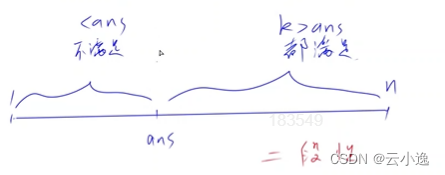
在这里插入图片描述
假设ans为正确答案【最小的k】，故小于ans都是不合法的，大于ans都是合法的。故其具有二段性，那么就可以使用二分法来二分出分界点了，这样可以把上面的暴力法的第一次循环改为二分，这样复杂度就变成了O(n³logn)。
继续分析：
我们题意是想统计每一个串是否只出现一次，然而判断一个东西只出现一次，可以使用哈希表，
将每一个串映射到哈希表里，然后判断每一串是否只出现一次，这样可以再去掉一个循环，复杂度变成O(n²logn);

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>

using namespace std;

int n;
string str;
unordered_set<string> S;

bool check(int mid)
{
    S.clear();
    for (int i = 0; i + mid - 1 < n; i ++ )
    {
        string s = str.substr(i, mid);
        if (S.count(s)) return false;
        S.insert(s);
    }

    return true;
}

int main()
{
    cin >> n >> str;

    int l = 1, r = n;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }

    cout << r << endl;

    return 0;
}